三维空间刚体运动4-1：四元数表示变换（各形式相互转换加代码——下篇）

序：本篇系列文章参照高翔老师《视觉SLAM十四讲从理论到实践》，讲解三维空间刚体运动，为读者打下坚实的数学基础。博文将原第三讲分为五部分来讲解，其中四元数部分较多较复杂，又分为四部分。如果读者急于实践，可直接阅读第五部分的机器人运动轨迹，此部分详细讲解了安装准备工作。此系列总体目录如下：

1. 旋转矩阵和变换矩阵；
2. 旋转向量表示旋转；
3. 欧拉角表示旋转；
4. 四元数包括以下部分：
   4-1.1 四元数表示变换——上篇；
   4-1.2 四元数表示变换——下篇；
   4-2. 四元数线性插值方法：LinEuler/LinMat/Lerp/Nlerp/Slerp；
   4-3. 四元数多点插值方法：Squad；
   4-4. 四元数多点连续解析解插值方法：Spicv；
   4-5. 四元数多点离散数值解插值方法：Sping。
5. 实践：SLAM中显示机器人运动轨迹及相机位姿。

4. 四元数到其它旋转表示的相互转换

任意单位四元数描述了一个旋转，该旋转也可用旋转向量、旋转矩阵或欧拉角描述。现在来考察四元数与旋转向量、旋转矩阵以及欧拉角的相互转换关系。

4.1 旋转向量

本节介绍旋转向量与四元数之间的转换关系。
绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。假设已知等效旋转轴方向单位旋转向量$u$的坐标为$u=\left[\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right]$，旋转角为$\theta$。根据3.2.3推导的定理3D旋转公式（一般情况四元数型），设其等效的单位四元数为$q=[q_0,q_1,q_2,q_3]$，则有：$$\{\begin{array}{c}{q}_0=cos(\frac{1}{2}\theta )\\ q_1=u_{x}sin(\frac{1}{2}\theta )\\ q_2=u_{y}sin(\frac{1}{2}\theta )\\ q_3=u_{z}sin(\frac{1}{2}\theta )\end{array}\text{\hspace{1em}(4.1)}$$
同理，当已知单位四元数$q=[q_0,q_1,q_2,q_3]$，其对应的旋转角$\theta$和旋转向量$u$为：$$\{\begin{array}{c}\theta =2\arccos q_0\\ [u_x,u_y,u_z{]}^T=[q_1,q_2,q_3{]}^T/\sin (\frac{\theta }{2})\end{array}\text{\hspace{1em}(4.2)}$$

4.2 旋转矩阵

已知单位四元数$q$，根据博文《三维空间刚体运动2：旋转向量与罗德里格斯公式》中的罗德里格斯公式展开式（2.3）及本文公式（4.2），将单位旋转向量$u$及旋转角$\theta$替换为单位四元数$q$，省去计算过程，得到单位四元数到旋转矩阵的转换公式为：$$R=\left[\begin{array}{ccc}1-2q_2^2-2q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& 1-2q_1^2-2q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_0{q}_1)& 1-2q_1^2-2q_2^2\end{array}\right]\text{\hspace{1em}(4.3)}$$
假设已知变换矩阵：$$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$根据公式（4.3），推导对应的单位四元数为：$$\{\begin{array}{c}{q}_0=\frac{1}{2}\sqrt{1+r_{11}+r_{22}+r_{33}}\\ q_1=\frac{r_{32}-r_{23}}{4q_0}\\ q_2=\frac{r_{13}-r_{31}}{4q_0}\\ q_3=\frac{r_{21}-r_{12}}{4q_0}\end{array}\text{\hspace{1em}(4.4)}$$

4.3 欧拉角

4.3.1 转换关系

那么将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转α,β,γ角）转换为四元数：$$q=\left[\begin{array}{c}\cos \frac{\gamma }{2}\\ 0\\ 0\\ \sin \frac{\gamma }{2}\end{array}\right]\left[\begin{array}{c}\cos \frac{\beta }{2}\\ 0\\ \sin \frac{\beta }{2}\\ 0\end{array}\right]\left[\begin{array}{c}\cos \frac{\alpha }{2}\\ \sin \frac{\alpha }{2}\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \sin \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}-\cos \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \cos \frac{\alpha }{2}\sin \frac{\beta }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\cos \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \cos \frac{\alpha }{2}\cos \frac{\beta }{2}\sin \frac{\gamma }{2}-\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\cos \frac{\gamma }{2}\end{array}\right]$$
根据上面的公式可以求出逆解，即由四元数$q=(q_0,q_1,q_2,q_3)$到欧拉角的转换为：$$\left[\begin{array}{c}\alpha \\ \beta \\ \gamma \end{array}\right]=\left[\begin{array}{c}atan2(2(q_0{q}_1+q_2{q}_3),1-2(q_1^2+q_2^2))\\ \arcsin (2(q_0{q}_2-q_1{q}_3)\\ atan2(2(q_0{q}_3+q_1{q}_2),1-2(q_2^2+q_3^2))\end{array}\right]$$这里使用了$atan2(y,x)$而不是$arctan(\frac{y}{x})$，因为$arctan(\frac{y}{x})$的取值范围为$[-\frac{\pi }{2},\frac{\pi }{2}]$，只有$180°$，而绕某个轴旋转时范围是$360°$，$atan2(y,x)$正好满足需求。$atan2(y,x)$是一个函数，在C语言里返回的是指方位角，函数原型为$doubleatan2(doubley,doublex)$ ，返回以弧度表示的 $y/x$ 的反正切。y 和 x 的值的符号决定了正确的象限。也可以理解为计算复数$x+yi$ 的辐角，计算时atan2 比 atan 稳定。

4.3.2 转换中的万象锁问题

另外需要注意的就是奇异性问题，即万向锁，下面分析这种情况。当刚体绕Y轴旋转了$90°$（俯仰角pitch=90）时，如何计算横滚角roll和偏航角yaw？这时会发生自由度丢失的情况，即Yaw和Roll会变为一个自由度。此时再使用上面的公式根据四元数计算欧拉角会出现问题：$\arcsin (2(q_0{q}_2-q_1{q}_3)$的定义域为$[-1,1]$，当$2(q_0{q}_2-q_1{q}_3)=\pm 0.5$时（在程序中浮点数不能直接进行等于判断，要使用合理的阈值），俯仰角$\beta$为$\pm 90°$，将其带入正向公式计算出四元数$(q_0,q_1,q_2,q_3)$，然后可以发现逆向公式中atan2函数中的参数全部为0，即出现了$\frac{0}{0}$的情况！无法计算。
当$\beta =90°$时，$\sin \frac{\beta }{2}=\cos \frac{\beta }{2}=0.707$，将其带入公式中有：$$q=\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]=\left[\begin{array}{c}0.707(\cos \frac{\alpha }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\sin \frac{\alpha }{2}\cos \frac{\gamma }{2}-\cos \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\cos \frac{\alpha }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\cos \frac{\alpha }{2}\sin \frac{\gamma }{2}-\sin \frac{\alpha }{2}\cos \frac{\gamma }{2})\end{array}\right]=\left[\begin{array}{c}0.707\cos \frac{\alpha -\gamma }{2}\\ 0.707\sin \frac{\alpha -\gamma }{2}\\ 0.707\cos \frac{\alpha -\gamma }{2}\\ -0.707\sin \frac{\alpha -\gamma }{2}\end{array}\right]$$则$\frac{q_1}{q_0}=-\frac{q_3}{q_2}=\tan \frac{\alpha -\gamma }{2}$，于是有：$$\alpha -\gamma =2atan2(q_1,q_0)$$通常令$\alpha =0$，这时$\gamma =-2atan2(q_1,q_0)$。当俯仰角$\beta$为-90°，即刚体竖直向下时的情况也与之类似，可以推导出奇异姿态时的计算公式。
将四元数转换为欧拉角的代码可以参考附件。需要注意欧拉角有12种旋转次序，而上面推导的公式是按照Z-Y-X顺序进行的，所以有时会在网上看到不同的转换公式（因为对应着不同的旋转次序），在使用时一定要注意旋转次序是什么。比如ADAMS软件里就默认Body 3-1-3次序，即Z-X-Z欧拉角，而VREP中则按照X-Y-Z欧拉角旋转。另外万向锁问题代码的Z-Y-X欧拉角代码见类CameraSpacePoint。

5. 四元数的其他性质

为更全面理解四元数和方便引入slerp插值，这一节补充四元数的其它性质：旋转复合、双倍覆盖和指数形式。

5.1 旋转的复合

旋转的复合其实在我们之前证明$q^2=qq=[cos(2\theta ),sin(2\theta )u]$的时候就已经涉及到一点了，但是这里我们考虑的是更一般的情况。
假设有两个表示沿着不同轴、不同角度旋转的四元数$q_1、q_2$。首先，我们实施 $q_1$的变换，变换之后的$v^{{}^{\prime }}$为$$v^{{}^{\prime }}=q_{1}v{q}_1^{\ast }$$接下来，对$v^{{}^{\prime }}$进行$q_2$的变换，得到$v^{{}^{\prime \prime }}$：$$v^{{}^{\prime \prime }}=q_2{v}^{{}^{\prime }}{q}_2^{\ast }=q_2{q}_{1}v{q}_1^{\ast }{q}_2^{\ast }=q_{net}v{q}_{net}^{\ast }$$其中$q_{net}=q_2{q}_1$，另外写成上面的形式，还用到性质$q_1^{\ast }{q}_2^{\ast }=(q_2{q}_1{)}^{\ast }$。
注意四元数乘法的顺序，这和矩阵、复数的复合非常相似，都是从右向左叠加。另外要注意的是，$q_1$与$q_2$的等价旋转$q_{net}$并不是沿着$q_1$与$q_2$的两个旋转轴进行的两次旋转，它是沿着一个全新的旋转轴进行的一个等价旋转，仅仅只有旋转的结果相同。

5.2 双倍覆盖

四元数与 3D 旋转的关系并不是一对一的，同一个 3D 旋转可以使用两个不同的四元数来表示．对任意的单位四元数$q=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，$q$与$-q$代表的是同一个旋转。如果$q$表示的是沿着旋转轴$u$旋转$\theta$度，那么$-q$代表的是沿着相反的旋转轴$-u$旋转$(2\pi -\theta )$，负负得正：$$\begin{array}{rl}-q& =[-cos(\frac{1}{2}\theta ),-sin(\frac{1}{2}\theta )u]\\ & =[cos(\pi -\frac{1}{2}\theta ),sin(\pi -\frac{1}{2}\theta )(-u)]\end{array}$$所以，这个四元数旋转的角度为$2(\pi -\frac{1}{2}\theta )=2\pi -\theta$，从下面的图中我们可以看到，这两个旋转是完全等价的：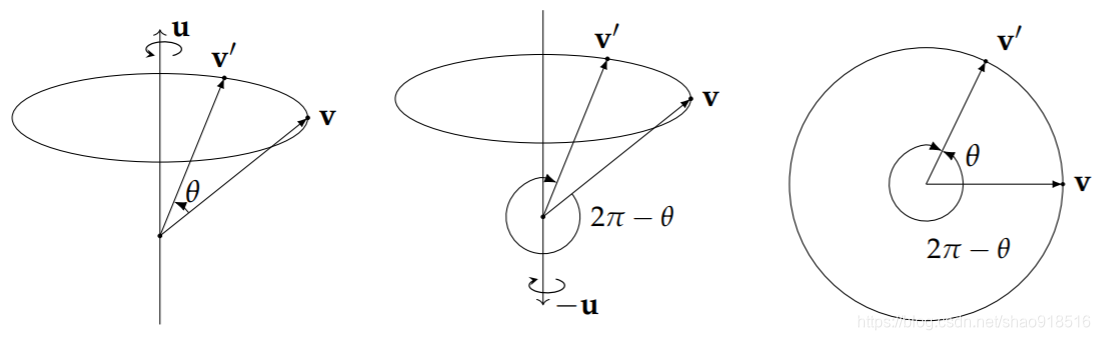
其实从四元数的旋转公式中也能推导出相同的结果：$$(-q)v(-q{)}^{\ast }=(-1{)}^{2}qv{q}^{\ast }=qv{q}^{\ast }$$所以，我们经常说单位四元数与3D旋转有一个「2对1满射同态」(2-1 Surjective Homomorphism) 关系，或者说单位四元数双倍覆盖(Double Cover)了3D旋转。它的严格证明会用到一些李群的知识，这里不再拓展。
有一点需要注意的是，虽然$q$与$-q$是两个不同的四元数，但是由于旋转矩阵中的每一项都包含了四元数两个分量的乘积，它们的旋转矩阵是完全相同的，即旋转矩阵并不会出现双倍覆盖的问题。

5.3 指数形式

在讨论复数的时候，我们利用欧拉公式将2D的旋转写成了$v^{{}^{\prime }}=e^{i\theta v}$这样的指数形式。实际上，我们也可以利用四元数将 3D 旋转写成类似的形式。
类似于复数的欧拉公式，四元数也有一个类似的公式。如果$u$是一个单位向量，那么对于单位四元数$u_q=[0,u]$，有：$$e^{u\theta }=cos(\theta )+u_{q}sin(\theta )=cos(\theta )+usin(\theta )$$这也就是说，$q=[\cos (\theta ),\sin (\theta )u]$可以使用指数表示为$e^{u\theta }$。这个公式的证明与欧拉公式的证明非常类似，直接使用级数展开就可以了，这里不再扩展。
注意，因为$u$是一个单位向量，$u^2=[-u\cdot u,0]=-\Vert u{\Vert }^2=-1$．这与欧拉公式中的$i$是非常类似的。有了指数型的表示方式，我们就能够将之前四元数的旋转公式改写为指数形式了，由此可得到定义：
3D旋转公式（指数型）：任意向量$v$沿着以单位向量定义的旋转轴$u$旋转$\theta$角度之后的$v^{{}^{\prime }}$可以使用四元数的指数表示。令$w=[0,v],u_q=[0,u]$，那么：$$w^{{}^{\prime }}=e^{u_q\frac{\theta }{2}}v{e}^{-u_q\frac{\theta }{2}}$$有了四元数的指数定义，我们就能够定义四元数的更多运算了。首先是自然对数$log$，对任意单位四元数$q=[cos(\theta ),sin(\theta )u]=e^{u_q\theta }$：$$log(q)=log(e^{u_q\theta })=[0,u\theta ]$$接下来是单位四元数的幂运算：$$q^t=(e^{u_q\theta }{)}^t=e^{u_q(t\theta )}=[cos(t\theta ),sin(t\theta )u]$$可以看到，一个单位四元数的$t$次幂等同于将它的旋转角度缩放至$t$倍，并且不会改变它的旋转轴（$u$必须是单位向量，所以一般不能与$t$结合）。这些运算会在之后讨论四元数插值时非常有用。限于篇幅，四元数插值的讲解见下一篇博客《三维空间刚体运动4-2：四元数插值（lerp，Nlerp，Slerp，Squad等）》

5.4 幂函数性质

上面给出四元数的指数形式后，可推导出一个重要的指函数性质，这一性质下一篇将用到。首先看推论：
四元数推论1 ：设$q\in {\mathbb{H}}_1,p=[a,b\mathbf{v}]$，其中$a,b,r\in \mathbb{R},\mathbf{v}\in {\mathbb{R}}^3$，如果$q[r,\mathbf{v}]q^{\ast }=[r,{\mathbf{v}}^{{}^{\prime }}]$，那么$q[a,b\mathbf{v}]q^{\ast }=[a,b{\mathbf{v}}^{{}^{\prime }}]$。
推论证明：$$\begin{array}{rl}qp{q}^{\ast }& =q[a,b\mathbf{v}]q^{\ast }\\ & =qb[\frac{a}{b},\mathbf{v}]q^{\ast }\\ & =b[\frac{a}{b},{\mathbf{v}}^{{}^{\prime }}]\\ & =[a,b{\mathbf{v}}^{{}^{\prime }}]\end{array}$$根据推论，得出以下定理：
四元数定理2 ：设$q,p\in {\mathbb{H}}_1,p=[\cos \theta ,\sin \theta \mathbf{v}],t\in \mathbb{R}$，那么$q{p}^t{q}^{\ast }=(qp{q}^{\ast }{)}^t$。
定理证明：
根据推论，存在${\mathbf{v}}^{{}^{\prime }}\in {\mathbb{R}}^3$，使得$q[\cos \theta ,\sin \theta \mathbf{v}]q^{\ast }=[\cos \theta ,\sin \theta {\mathbf{v}}^{{}^{\prime }}]$，因此得到：$$\begin{array}{rl}q{p}^t{q}^{\ast }& =q(\exp (t\log p))q^{\ast }\\ & =q(\exp (t[0,\theta \mathbf{v}]))q^{\ast }\\ & =q(\exp [0,t\theta \mathbf{v}])q^{\ast }\\ & =q([\cos t\theta ,\sin t\theta \mathbf{v}])q^{\ast }\\ & =[\cos t\theta ,\sin t\theta {\mathbf{v}}^{{}^{\prime }}]\\ & =\exp (t[0,\theta {\mathbf{v}}^{{}^{\prime }}])\\ & =\exp (t\log [\cos \theta ,\sin \theta {\mathbf{v}}^{{}^{\prime }}])\\ & =\exp (t\log (qp{q}^{\ast }))\\ & =(qp{q}^{\ast }{)}^t\end{array}$$
至此，四元数表示旋转的理论部分讲解完了。

6. 实践

现在，我们通过两个小程序实际演练四元数的运算。其中四元数的基础运算和高阶运算程序实现放在下一讲Slerp中。

6.1 四元数旋转运算

第一个小程序是演示四元数的常规运算，包括与旋转矩阵、旋转向量的转换，以及用四元数旋转一个向量，如下所示：

#include<iostream>
#include<cmath>
using namespace std;#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>using namespace Eigen;int main(int argc, char **argv){//Eigen/Geometry模块提供了各种旋转和平移的表示，3D旋转矩阵直接使用Matrix3d或Matrix3fMatrix3d rotation_matrix = Matrix3d::Identity();//旋转向量使用AngleAxis，它底层不直接是Matrix，但运算可以当做矩阵，因为重载了运算符AngleAxisd rotation_vector(M_PI/4, Vector3d(0, 0, 1));//设置输出精度cout.precision(3);cout<<"rotation matrix =\n"<<rotation_matrix<<endl;cout<<"rotation vector =\n"<<rotation_vector.matrix()<<endl;//旋转向量转换的矩阵可以直接赋值给旋转矩阵rotation_matrix = rotation_vector.toRotationMatrix();cout<<"rotation vector to Matrix =\n"<<rotation_matrix<<endl;//旋转向量Vector3d v(1, 0, 0);cout<<"v = "<<v.transpose()<<endl;//四元数，可以直接把AngleAxis赋值给四元数，反之亦然Quaterniond q = Quaterniond(rotation_vector);//coeffs:多项式系数（coefficients)，其顺序为(x,y,z,w)，w为实部，xyz为虚部cout<<"quaternion from rotation vector = "<<q.coeffs().transpose()<<endl;//也可以直接把旋转矩阵赋给它q = Quaterniond(rotation_matrix);cout<<"quaternion from rotation matrix = "<<q.coeffs().transpose()<<endl;//使用四元数旋转一个向量，使用重载的乘法即可//注意q*v在数学上是qvq^{-1}v_rotated = q*v;cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;//用常规向量乘法表示qvq^{-1}，则计算如下：Quaterniond q_rotate_v = q*Quaterniond(0,1,0,0)*q.inverse();cout<<"should be equal to "<<q_rotate_v.coeffs().transpose()<<endl;return 0;

输出结果如下：

rotation matrix =
1 0 0
0 1 0
0 0 1
rotation vector =0.707 -0.707      00.707  0.707      00      0      1
rotation vector to Matrix =0.707 -0.707      00.707  0.707      00      0      1
v = 1 0 0
v transofrmed = 1.71 3.71    4
quaternion from rotation vector =     0     0 0.383 0.924
quaternion from rotation matrix =     0     0 0.383 0.924
(1,0,0) after rotation = 0.707 0.707     0
should be equal to 0.707 0.707     0     0

请读者注意，程序代码通常和数学表示有一些细微的差别。例如，通过运算符重载，四元数和三维向量可以直接计算乘法，但在数学上则需要先把向量转成虚四元数，再利用四元数乘法进行计算，同样的情况也适用于变换矩阵乘三维向量的情况。总体而言，程序中的用法会比数学公式更灵活。

6.2 坐标变换

下面我们举一个小例子来演示坐标变换。
例子：设有小萝卜一号和小萝卜二号位于世界坐标系中。记世界坐标系为$W$，小萝卜们的坐标系分别为$R_1$和$R_2$。小萝卜一号的位姿为$q_1=[0.35,0.2,0.3,0.1{]}^T$，$t_1=[0.3,0.1,0.1{]}^T$。小萝卜二号的位姿为$q_2=[-0.5,0.4,-0.1,0.2{]}^T$，$t_2=[-0.1,0.5,0.3{]}^T$。这里的$q$和$t$表达的是$T_{R_k,W},k=1,2$，也就是世界坐标系到相机坐标系的变换关系。现在，小萝卜一号看到某个点在自身的坐标系下坐标为$p_{R_1}=[0.5,0,0.2{]}^T$，求该向量在小萝卜二号坐标系下的坐标。
这是一个非常简单，但又具有代表性的例子。在实际场景中你经常需要在同一个机器人的不同部分，或者不同机器人之间转换坐标。计算过程也很简单，只需计算：$$p_{R_2}=T_{R_2,W}{T}_{W,R_1}{p}_{R_1}$$下面请看程序：

#include<iostream>
#include<vector>
#include<algorithm>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>using namespace std;
using namespace Eigen;int main(int argc, char** argv){//位姿四元数q1,q2Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);cout<<"q1.coeffs=\n"<<q1.coeffs()<<endl;cout<<"q2.coeffs=\n"<<q2.coeffs()<<endl;//四元数转换为旋转矩阵cout<<"q1.matrix=\n"<<q1.matrix()<<endl;cout<<"q2.matrix=\n"<<q2.matrix()<<endl;//归一化，转换为单位四元数q1.normalize();q2.normalize();cout<<"q1.normalize="<<q1.matrix()<<endl;cout<<"q2.normalize="<<q2.matrix()<<endl;//位移向量t1,t2,小萝卜一号下的坐标pr1Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);Vector3d pr1(0.5, 0, 0.2);//Eigen::Isometry3d:欧式变换矩阵4*4Isometry3d Twr1(q1), Tr2w(q2);cout<<"Twr1.matrix="<<Twr1.matrix()<<endl;cout<<"Tr2w.matrix="<<Tr2w.matrix()<<endl;//坐标转换，计算T=Ra+tTwr1.pretranslate(t1);Tr2w.pretranslate(t2);//先将pr1转换为世界坐标系，然后转换为小萝卜二号下的坐标pr2Vector3d pr2 = Tr2w * Twr1.inverse()*pr1;cout<<"pr2.transpose="<<pr2.transpose()<<endl;return 0;
}

输出结果如下：

q1.coeffs=0.20.30.1
0.35
q2.coeffs=0.4
-0.10.2
-0.5
q1.matrix=0.8  0.05  0.250.19   0.9 -0.08
-0.17   0.2  0.74
q2.matrix=0.9  0.12  0.26
-0.28   0.6  0.360.06 -0.44  0.66
q1.normalize=0.238095   0.190476   0.9523810.72381   0.619048  -0.304762-0.647619   0.761905 0.00952381
q2.normalize=0.782609   0.26087  0.565217
-0.608696  0.130435  0.7826090.130435 -0.956522   0.26087
Twr1.matrix=0.238095   0.190476   0.952381          00.72381   0.619048  -0.304762          0-0.647619   0.761905 0.00952381          00          0          0          1
Tr2w.matrix=0.782609   0.26087  0.565217         0
-0.608696  0.130435  0.782609         00.130435 -0.956522   0.26087         00         0         0         1
pr2.transpose=
-0.0309731    0.73499   0.296108

四元数的第一部分讲解到此。

本文基于《视觉SLAM十四讲：从理论到实践》和《Quaternions, Interpolation and Animation》编写，但相对于原文会适当精简，同时为便于全面理解，会收集其他网络好文，根据作者理解，加入一些注解和扩展知识点，如果您觉得还不错，请一键四连（点赞关注收藏评论），让更多的人看到。

参考文献：

1. 《视觉SLAM十四讲：从理论到实践》，高翔、张涛等著，中国工信出版社
2. Quaternions, Interpolation and Animation
3. 四元数与三维旋转
4. 四元数与欧拉角（RPY角）的相互转换
5. 如何形象地理解四元数？