【C++】青蛙跳跃问题解析与解法

文章目录
- 💯前言
- 💯题目描述
- 第一部分:基本青蛙过河问题
- 第二部分:石柱和荷叶问题
- 💯解题思路与分析
- 第一部分:青蛙过河问题
- 解法思路:递归拆解
- 第二部分:最多能跳多少只青蛙
- 思路与公式推导
- 💯代码实现
- 递归函数实现
- 示例输出
- 💯递归的理解与优化
- 优化思路
- 💯小结

💯前言
- 青蛙跳跃问题是一道经典的递归与路径优化题目,考察了递归思维、问题分解能力以及逻辑推理能力。在本篇文章中,我们将详细分析题目的背景、题目规则、解决方案、代码实现以及优化思路。
通过逐步拆解问题和总结规律,帮助读者深入理解递归的本质以及其在路径问题中的应用。本文不仅关注基本解法,还会深入探讨题目的扩展性和优化空间,力求帮助读者掌握这种递归思维在实际问题中的应用。
C++ 参考手册

💯题目描述
本题分为两个部分,分别如下:
第一部分:基本青蛙过河问题
题目背景:
(2000年全国青少年信息学奥林匹克试题)
一条小溪尺寸不大,青蛙可以从左岸跳到右岸。在左岸有一石柱 L,面积只容得下一只青蛙落脚;同样,右岸也有一石柱 R,面积也只容得下一只青蛙落脚。有一队青蛙从尺寸上一个比一个小。我们将青蛙从小到大,用 1, 2, …, n 编号。
要求:
- 初始时青蛙只能跳到左岸的石柱 L 上,按编号一个落一个,小的青蛙落在大的青蛙上面。不允许大的在小的上面。
- 将所有青蛙从 L 移动到 R,保持大小顺序不变。
分析重点:
这个问题与经典的汉诺塔问题极其相似,可以通过递归来解决。我们需要借助中间的石柱或荷叶,逐步将青蛙从左岸移动到右岸。
第二部分:石柱和荷叶问题
新增规则:
- 青蛙从左岸 L 跳出后,不允许再跳回左岸。
- 青蛙跳到右岸 R 或中途的荷叶/石柱后,也不能再离开。
已知条件:
- 溪中有 ( s ) 根石柱和 ( y ) 片荷叶。
目标:求 最多能跳过多少只青蛙。
💯解题思路与分析
第一部分:青蛙过河问题
这个问题的解决思路与 汉诺塔问题 极其相似。汉诺塔问题是一种经典的递归问题,通过将盘子逐个移动来达到最终目标。在青蛙过河问题中,我们将递归思想进行迁移,借助中间位置完成青蛙的转移。
解法思路:递归拆解
-
基本思路:将青蛙分为两部分。
- 先将 ( n-1 ) 只青蛙从 L 移动到辅助位置(荷叶/石柱)。
- 然后将第 ( n ) 只青蛙直接从 L 移动到 R。
- 最后将 ( n-1 ) 只青蛙从辅助位置移动到 R。
-
递归关系可以总结为:
T ( n ) = 2 ⋅ T ( n − 1 ) + 1 T(n) = 2 \cdot T(n-1) + 1 T(n)=2⋅T(n−1)+1
其中 ( T(n) ) 是将 ( n ) 只青蛙移动到右岸所需的最少步数。 -
递归终止条件:当只剩下一只青蛙时,直接将其移动到目标位置。这一步与汉诺塔的最小子问题完全一致,青蛙跳到终点即可。
-
路径可视化:
递归的核心在于分解问题。可以通过树形结构将每一步的移动过程展示出来,使得解法更加清晰直观。
第二部分:最多能跳多少只青蛙
思路与公式推导
新增了 石柱 和 荷叶 后,溪中的路径可以看作是多次跳跃的落脚点。题目要求青蛙跳到这些落脚点后不能再移动,问题变为:
- 每次增加一个石柱时,路径数量会 翻倍。
- 荷叶提供了额外的停留点。
关键分析:
- 当 ( s = 0 )(无石柱)时,最多能跳过的青蛙数量为:
k = y + 1 k = y + 1 k=y+1
其中 ( y ) 是荷叶数量,右岸 ( R ) 也算一个位置。 - 当 ( s > 0 )(有石柱)时,每增加一根石柱,路径会 翻倍,满足以下递归关系:
k = 2 ⋅ e x t J u m p ( s − 1 , y ) k = 2 \cdot ext{Jump}(s-1, y) k=2⋅extJump(s−1,y) - 最终递归公式可以总结为:
k = 2 s ⋅ ( y + 1 ) k = 2^s \cdot (y + 1) k=2s⋅(y+1)
其中:- ( s ) 是石柱数。
- ( y ) 是荷叶数。
- ( 2^s ) 表示路径翻倍的次数。
💯代码实现
递归函数实现
#include <iostream>
using namespace std;// 递归函数:计算最多能跳过多少只青蛙
int Jump(int s, int y) {int k = 0; // 结果变量if (s == 0) // 递归终止条件k = y + 1; // 没有石柱,直接加上荷叶数和右岸elsek = 2 * Jump(s - 1, y); // 每增加一根石柱,路径翻倍return k; // 返回结果
}int main() {int s, y; // 定义变量cout << "请输入溪中的石柱数 s 和荷叶数 y:" << endl;cin >> s >> y; // 输入石柱数和荷叶数int result = Jump(s, y); // 调用函数cout << "最多能跳过的青蛙数为:" << result << endl; // 输出结果return 0;
}

示例输出
假设输入:
请输入溪中的石柱数 s 和荷叶数 y:
3 2
程序输出:
最多能跳过的青蛙数为:24
验证:
根据公式 ( k = 2^s \cdot (y + 1) ):
- ( s = 3 ),( y = 2 ):
k = 2 3 ⋅ ( 2 + 1 ) = 8 ⋅ 3 = 24 k = 2^3 \cdot (2 + 1) = 8 \cdot 3 = 24 k=23⋅(2+1)=8⋅3=24
💯递归的理解与优化
递归是一种通过将大问题分解为小问题逐步解决的方法。在本题中:
- 终止条件:当 ( s = 0 ) 时,直接求解。
- 递归关系:路径翻倍,通过 ( k = 2 \cdot Jump(s-1, y) ) 实现。
优化思路
如果问题规模较大(例如 ( s ) 很大),递归会占用较多栈空间。可以使用 迭代法 替代递归,将结果逐步累积:
int JumpIterative(int s, int y) {int k = y + 1; // 初始值,当 s = 0 时for (int i = 0; i < s; ++i) {k *= 2; // 每增加一根石柱,路径翻倍}return k;
}
💯小结

通过本题,我们深入理解了递归的本质和路径问题的解法:
- 青蛙过河问题 与 汉诺塔问题 类似,通过递归分解问题逐步求解。
- 在 石柱和荷叶问题 中,路径数量随着石柱数 ( s ) 指数级增长,满足公式:
k = 2 s ⋅ ( y + 1 ) k = 2^s \cdot (y + 1) k=2s⋅(y+1) - 提供了递归和迭代两种解法,递归结构清晰,迭代更高效。
- 通过图示和示例输出,直观展示了问题的解决过程。
掌握这类问题的解法,有助于培养递归思维和问题分解能力,为解决更复杂的算法问题打下坚实的基础。这类问题也为动态规划和搜索算法提供了重要的学习基础。

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
相关文章:

【C++】青蛙跳跃问题解析与解法
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述第一部分:基本青蛙过河问题第二部分:石柱和荷叶问题 💯解题思路与分析第一部分:青蛙过河问题解法思路:递…...

自动驾驶AVM环视算法--python版本的俯视TOP投影模式
c语言版本和算法原理的可以查看本人的其他文档。《自动驾驶AVM环视算法--全景的俯视图像和原图》本文档进用于展示部分代码的视线,获取方式网盘自行获取(非免费介意勿下载):链接: https://pan.baidu.com/s/1MJa8ZCEfNyLc5x0uVegto…...

Go 语言与时间拳击理论下的结对编程:开启高效研发编程之旅
一、引言 结对编程作为一种软件开发方法,在提高代码质量、增强团队协作等方面具有显著优势。而时间拳击理论为结对编程带来了新的思考角度。本文将以 Go 语言为中心,深入探讨时间拳击理论下的结对编程。 在当今软件开发领域,高效的开发方法和…...
Qt+OPC开发笔记(一):OPCUA介绍、open62541介绍、编译与基础环境Demo
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/144516882 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
ElasticSearch 常见故障解析与修复秘籍
文章目录 一、ElasticSearch启动服务提示无法使用root用户二、ElasticSearch启动提示进程可拥有的虚拟内存少三、ElasticSearch提示用户拥有的可创建文件描述符太少四、ElasticSearch集群yellow状态分析五、ElasticSearch节点磁盘使用率过高,read_only状态问题解决六…...
序列模型的使用示例
序列模型的使用示例 1 RNN原理1.1 序列模型的输入输出1.2 循环神经网络(RNN)1.3 RNN的公式表示2 数据的尺寸 3 PyTorch中查看RNN的参数4 PyTorch中实现RNN(1)RNN实例化(2)forward函数(3…...

对rust的全局变量使用drop方法
文章目录 rust处理全局变量的策略方法1:在main中自动Drop全局变量 参考 rust处理全局变量的策略 Rust 的静态变量不会在程序退出时自动调用 Drop,因为它们的生命周期与进程绑定。 use std::sync::OnceLock;struct GlobalData {content: String, }impl …...

Node.js教程入门第一课:环境安装
对于一个程序员来说,每学习一个新东西的时候,第一步基本上都是先进行环境的搭建! 从本章节开始让我们开始探索Node.js的世界吧! 什么是Node.js? 那么什么是Node.js呢?简单的说Node.js 就是运行在服务端的 JavaScript JavaScript…...
Visual Studio 使用 GitHub Copilot 扩展
🎀🎀🎀【AI辅助编程系列】🎀🎀🎀 Visual Studio 使用 GitHub Copilot 与 IntelliCode 辅助编码Visual Studio 安装和管理 GitHub CopilotVisual Studio 使用 GitHub Copilot 扩展Visual Studio 使用 GitHu…...

【Qualcomm】IPQ5018获取TR069 WiFi 接口Stats状态方法
IPQ5018 简介 IPQ5018 是高通(Qualcomm)公司推出的一款面向网络设备的系统级芯片(SoC)。它通常用于路由器、接入点和其他网络设备中,提供高性能的无线网络连接。以下是关于 IPQ5018 的一些关键特性和功能: 关键特性 高性能处理器 IPQ5018 集成了多核 CPU,通常是 ARM …...

数字营销咨询,照亮企业营销数字化每一步
在快消品领域,面对市场竞争日益激烈的现状,营销端的数字化升级已经成为企业生意增长的重要驱动力。 然而,鉴于营销端数字化建设的高昂成本及其广泛覆盖的业务范畴,企业在启动此类项目之前,通常会遭遇一系列挑战与顾虑&…...
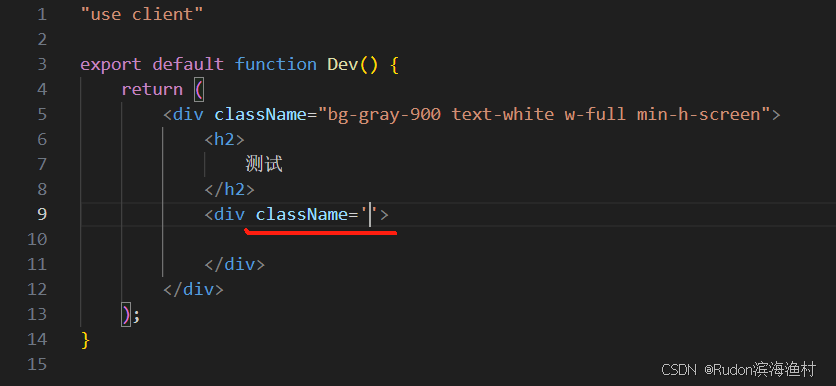
修改vscode中emmet中jsx和tsx语法中className的扩展符号从单引号到双引号 - HTML代码补全 - 单引号双引号
效果图 实现步骤 文件 > 首选项 > 设置搜索“”在settings.json中修改,增加 "emmet.syntaxProfiles": {"html": {"attr_quotes": "single"},"jsx": {"attr_quotes": "double","…...

【Cmake】
1 设置安装路径 -DCMAKE_INSTALL_PREFIX"安装路径"2 使用交叉编译 -DCMAKE_C_COMPILE"交叉编译器绝对路径"3 编译静态库 -DPAHO_BUILD_STARTTRUE...
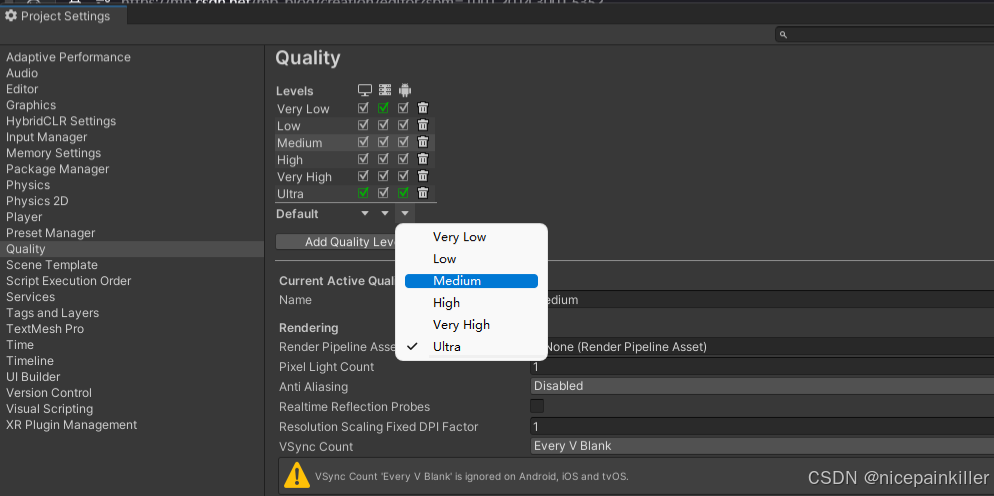
Flutter 内嵌 unity3d for android
前言: 最近刚整完 unity3d hybridCLR 更新代码和资源,我们 趁热打铁 将 Unity3D 嵌入 Flutter 应用中。实现在 Flutter 使用 Unity3D, 可以做 小游戏 大游戏; 之前都是 内嵌 Webview 来实现的。虽然 CocosCreator 做出来的效果也不错…...
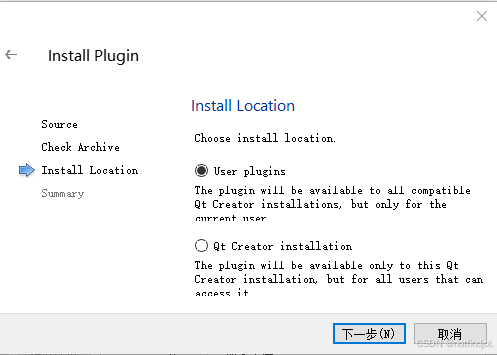
sqlite加密-QtCipherSqlitePlugin 上
1、下载并解压软件 https://download.csdn.net/download/notfindjob/90140129 2、编译(可支持Qt5.12编译) 3、安装插件...
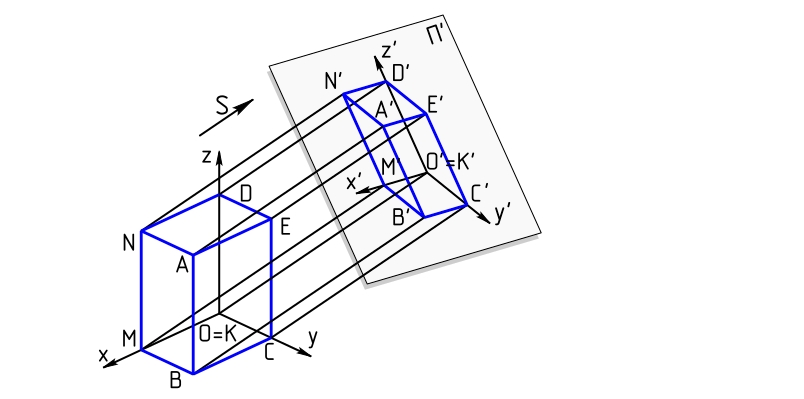
正交投影 (Orthographic Projection) 详解
正交投影 (Orthographic Projection) 详解 正交投影是一种将三维空间中的物体投影到二维平面上的方法,它在计算机图形学、建筑设计、工程绘图等领域中广泛应用。与透视投影不同,正交投影不会随着距离的变化而改变物体的大小,因此所有平行线在…...
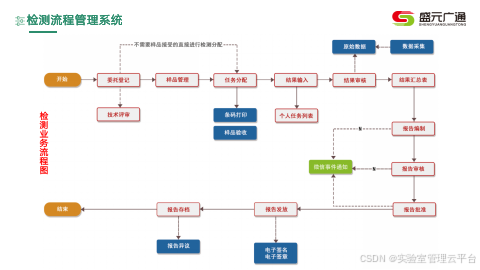
盛元广通畜牧与水产品检验技术研究所LIMS系统
一、系统概述 盛元广通畜牧与水产品检验技术研究所LIMS系统集成了检测流程管理、样品管理、仪器设备管理、质量控制、数据记录与分析、合规性管理等功能于一体,能够帮助实验室实现全流程的数字化管理。在水产、畜牧产品的质检实验室中,LIMS系统通过引入…...
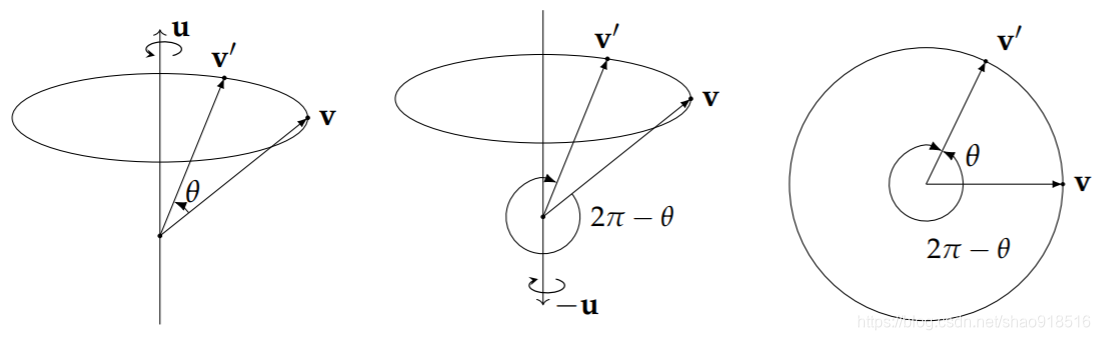
三维空间刚体运动4-1:四元数表示变换(各形式相互转换加代码——下篇)
三维空间刚体运动4-1:四元数表示变换(各形式相互转换加代码——下篇) 4. 四元数到其它旋转表示的相互转换4.1 旋转向量4.2 旋转矩阵4.3 欧拉角4.3.1 转换关系4.3.2 转换中的万象锁问题 5. 四元数的其他性质5.1 旋转的复合5.2 双倍覆盖5.3 指数…...

PyTorch如何通过 torch.unbind 和torch.stack动态调整张量的维度顺序
笔者一篇博客PyTorch 的 torch.unbind 函数详解与进阶应用:中英双语中有一个例子如下: # 创建一个 3x2x2 的三维张量 x torch.tensor([[[1, 2], [3, 4]],[[5, 6], [7, 8]],[[9, 10], [11, 12]]])# 第一步:沿第 0 维分解为 3 个 2x2 张量 un…...

【Unity3D】报错libil2cpp.so找不到问题
mainTemplate.gradle文件末尾添加: **IL_CPP_BUILD_SETUP** 此报错发生在低版本的Unity升级到高版本后,例如Unity2019升级到Unity2021,而Unity2019默认创建的mainTemplate.gradle文件是不包含**IL_CPP_BUILD_SETUP** 因此会导致libil2cpp.so…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
