P8615 拼接平方数 P8699 排列数
文章目录
- [蓝桥杯 2014 国 C] 拼接平方数
- [蓝桥杯 2019 国 B] 排列数
[蓝桥杯 2014 国 C] 拼接平方数
题目描述
小明发现 49 49 49 很有趣,首先,它是个平方数。它可以拆分为 4 4 4 和 9 9 9,拆分出来的部分也是平方数。 169 169 169 也有这个性质,我们权且称它们为:拼接平方数。
100 100 100 可拆分 1 , 00 1,00 1,00,这有点勉强,我们规定, 0 , 00 , 000 0,00,000 0,00,000 等都不算平方数。
小明想:还有哪些数字是这样的呢?
你的任务出现了:找到某个区间的所有拼接平方数。
输入格式
两个正整数 a , b ( a < b < 1 0 6 ) a,b(a<b<10^6) a,b(a<b<106)。
输出格式
若干行,每行一个正整数。表示所有的区间 [ a , b ] [a,b] [a,b] 中的拼接平方数,从小到大输出。
样例 #1
样例输入 #1
169 10000
样例输出 #1
169
361
1225
1444
1681
3249
4225
4900
9025
提示
时限 1 秒, 256M。蓝桥杯 2014 年第五届国赛
解题思路
我们可以直接从 a a a 开始遍历到到 b b b ,判断其是否是平方数,在该数字是平方数的情况下,将数字拆分去判断拆分出来的两部分数是否是平方数。
拆分数字可以将数字转成字符串,使用 s u b s t r substr substr 来拆分数字,再将得到的两个字符串用 s t o i stoi stoi 转成数字来判断是否是平方数。
include <bits/stdc++.h>
using namespace std;//判断数字是否为平方数
//一个数的平方根减去其小数部分为0,说明该数为平方数
bool check(int x)
{double d=sqrt(x)-(int)sqrt(x);return d==0.0;
}int main()
{int a,b;cin>>a>>b;for(int i=a;i<=b;++i){//在数字为平方数的情况下再去拆分数字if(check(i)){string str=to_string(i);for(int k=1;k<str.size();++k){string s1=str.substr(0,k),s2=str.substr(k);int p1=stoi(s1),p2=stoi(s2);//排除题目提及的0的特殊情况if(p2 == 0) break;//拆分出来的两个数也是平方数,说明i是拼接平方数if(check(p1)&&check(p2)){cout<<i<<endl;break;}}}}return 0;
}

[蓝桥杯 2019 国 B] 排列数
题目描述
在一个排列中,一个折点是指排列中的一个元素,它同时小于两边的元素,或者同时大于两边的元素。
对于一个 1 ∼ n 1 ∼ n 1∼n 的排列,如果可以将这个排列中包含 t t t 个折点,则它称为一个 t + 1 t + 1 t+1 单调排列。
例如,排列 ( 1 , 4 , 2 , 3 ) (1, 4, 2, 3) (1,4,2,3) 是一个 3 3 3 单调排列,其中 4 4 4 和 2 2 2 都是折点。
给定 n n n 和 k k k,请问 1 ∼ n 1 ∼ n 1∼n 的所有排列中有多少个 k k k 单调排列?
输入格式
输入一行包含两个整数 n n n, k k k。
输出格式
输出一个整数,表示答案。答案可能很大,你可需要输出满足条件的排列
数量除以 123456 123456 123456 的余数即可。
样例 #1
样例输入 #1
4 2
样例输出 #1
12
提示
对于 20 % 20 \% 20% 的评测用例, 1 ≤ k ≤ n ≤ 10 1 \leq k \leq n \leq 10 1≤k≤n≤10;
对于 40 % 40 \% 40% 的评测用例, 1 ≤ k ≤ n ≤ 20 1 \leq k \leq n \leq 20 1≤k≤n≤20; 对于 60 % 60 \% 60% 的评测用例, 1 ≤ k ≤ n ≤ 100 1 \leq k \leq n \leq 100 1≤k≤n≤100;
对于所有评测用例, 1 ≤ k ≤ n ≤ 500 1 \leq k \leq n \leq 500 1≤k≤n≤500 。
蓝桥杯 2019 年国赛 B 组 G 题。
解题思路
注意到题目给定的数据范围是 n ≤ 500 n \leq 500 n≤500 ,所以不能用暴力解法,很很明显我们要使用动态规划来解决这道问题。
d p [ i ] [ j ] dp[i][j] dp[i][j] 代表有 j j j 个节点的序列 1 ∼ i 1 ∼ i 1∼i 的排列个数。
接下来我们推状态转移方程:
在序列 1 ∼ i 1 ∼ i 1∼i 中插入第 i + 1 i + 1 i+1 个数,这个数比原序列的所有数都要大,并且这个数有 i + 1 i + 1 i+1 个位置可以插入。
- d p [ i + 1 ] [ j ] dp[i + 1][j] dp[i+1][j] 表示插入第 i + 1 i + 1 i+1 个节点后没有新增折点。
下面我们分情况讨论:
峰谷

峰谷峰

所以我们其实可以推出,折点数为 j j j ,插入第 i + 1 i + 1 i+1 个数后折点数不变的情况其实有 j + 1 j + 1 j+1 种。(谷峰谷、峰谷峰谷的情况都是这样)
故递推公式 d p [ i + 1 ] [ j ] + = d p [ i ] [ j ] × ( j + 1 ) dp[i + 1][j] += dp[i][j] \times (j + 1) dp[i+1][j]+=dp[i][j]×(j+1)
- d p [ i + 1 ] [ j + 1 ] dp[i + 1][j + 1] dp[i+1][j+1] 表示插入第 i + 1 i + 1 i+1 个节点后新增1个折点。
新增一个节点的情况很简单,只有序列两端是下降趋势,且插入位置是序列前后端才能新增一个节点,所以只有两种情况
故递归公式 d p [ i + 1 ] [ j + 1 ] + = d p [ i ] [ j ] × 2 dp[i + 1][j + 1] += dp[i][j] \times 2 dp[i+1][j+1]+=dp[i][j]×2
- d p [ i + 1 ] [ j + 2 ] dp[i + 1][j + 2] dp[i+1][j+2] 表示插入第 i + 1 i + 1 i+1 个节点后新增2个折点。
插入第 i + 1 i + 1 i+1 个数有 i + 1 i + 1 i+1 个位置可以插入,而增加折点的情况只有0个、1个、2个,所以新增2个折点的情况数我们可以用总的可插入位置个数减去上面提到的新增0个和1个折点的情况就能得到。
新增两个折点有 i + 1 − ( j + 1 ) − 2 = i − j − 2 i + 1 - (j + 1) - 2 = i - j - 2 i+1−(j+1)−2=i−j−2 种情况。

故递推公式 d p [ i + 1 ] [ j + 1 ] + = d p [ i ] [ j ] × ( i − j − 2 ) dp[i + 1][j + 1] += dp[i][j] \times (i - j - 2) dp[i+1][j+1]+=dp[i][j]×(i−j−2)
初始情况: d p [ 1 ] [ 0 ] = 0 dp[1][0] = 0 dp[1][0]=0 ,序列只有1个数0个折点的情况只有1种
d p [ i ] [ 0 ] = 2 ( 2 ≤ i ≤ n ) dp[i][0] = 2 (2 \leq i \leq n) dp[i][0]=2(2≤i≤n) , i i i 个数0个折点的情况是完全升序和完全降序两种情况。
最终答案为 d p [ n ] [ k − 1 ] dp[n][k - 1] dp[n][k−1] ( k − 1 k - 1 k−1个折点对应 k k k 单调序列)
#include <bits/stdc++.h>
using namespace std;int dp[505][505];
int n,k;
//得到的个数可能过大,需要取模处理
int mod(int x)
{return x%123456;
}int main()
{cin>>n>>k;dp[1][0]=1;for(int i=2;i<=n;++i){dp[i][0]=2;for(int j=0;j<=i;j++){//取模处理dp[i+1][j] += mod(dp[i][j]*(j+1));dp[i+1][j+1] += mod(dp[i][j]*2);dp[i+1][j+2] += mod(dp[i][j]*(i-j-2));}}cout<<dp[n][k-1]%123456<<endl;return 0;
}
相关文章:

P8615 拼接平方数 P8699 排列数
文章目录 [蓝桥杯 2014 国 C] 拼接平方数[蓝桥杯 2019 国 B] 排列数 [蓝桥杯 2014 国 C] 拼接平方数 题目描述 小明发现 49 49 49 很有趣,首先,它是个平方数。它可以拆分为 4 4 4 和 9 9 9,拆分出来的部分也是平方数。 169 169 169 也有…...
【C语言】拆解C语言的编译过程
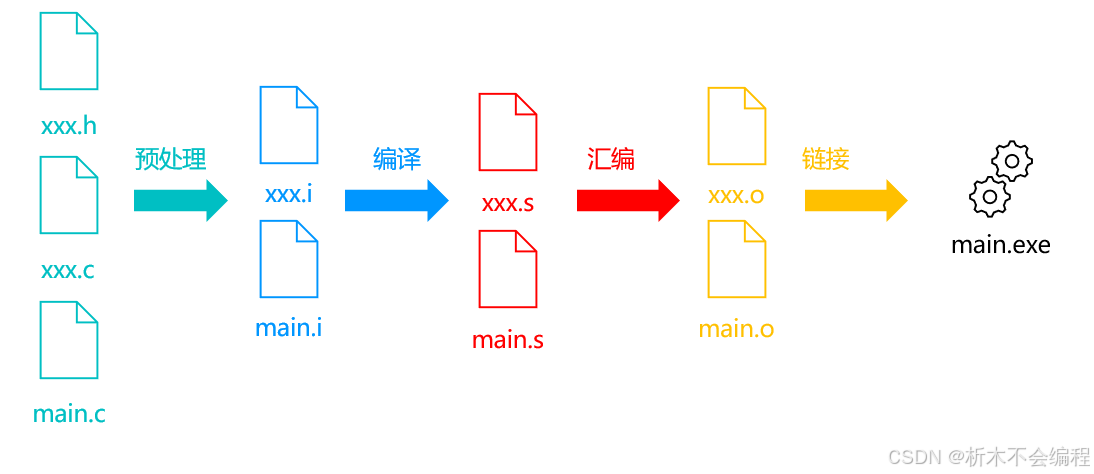
前言 学习C语言的过程中,涉及到各种各样的关键词,在我们点击编译的时候,都会做什么呢?让我们来拆解一下 C语言的编译过程 C语言的编译过程包括预处理、编译、汇编和链接四个主要步骤。每个步骤都有其特定的任务和输出文件类型&am…...

【C++】青蛙跳跃问题解析与解法
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述第一部分:基本青蛙过河问题第二部分:石柱和荷叶问题 💯解题思路与分析第一部分:青蛙过河问题解法思路:递…...

自动驾驶AVM环视算法--python版本的俯视TOP投影模式
c语言版本和算法原理的可以查看本人的其他文档。《自动驾驶AVM环视算法--全景的俯视图像和原图》本文档进用于展示部分代码的视线,获取方式网盘自行获取(非免费介意勿下载):链接: https://pan.baidu.com/s/1MJa8ZCEfNyLc5x0uVegto…...

Go 语言与时间拳击理论下的结对编程:开启高效研发编程之旅
一、引言 结对编程作为一种软件开发方法,在提高代码质量、增强团队协作等方面具有显著优势。而时间拳击理论为结对编程带来了新的思考角度。本文将以 Go 语言为中心,深入探讨时间拳击理论下的结对编程。 在当今软件开发领域,高效的开发方法和…...
Qt+OPC开发笔记(一):OPCUA介绍、open62541介绍、编译与基础环境Demo
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/144516882 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
ElasticSearch 常见故障解析与修复秘籍
文章目录 一、ElasticSearch启动服务提示无法使用root用户二、ElasticSearch启动提示进程可拥有的虚拟内存少三、ElasticSearch提示用户拥有的可创建文件描述符太少四、ElasticSearch集群yellow状态分析五、ElasticSearch节点磁盘使用率过高,read_only状态问题解决六…...
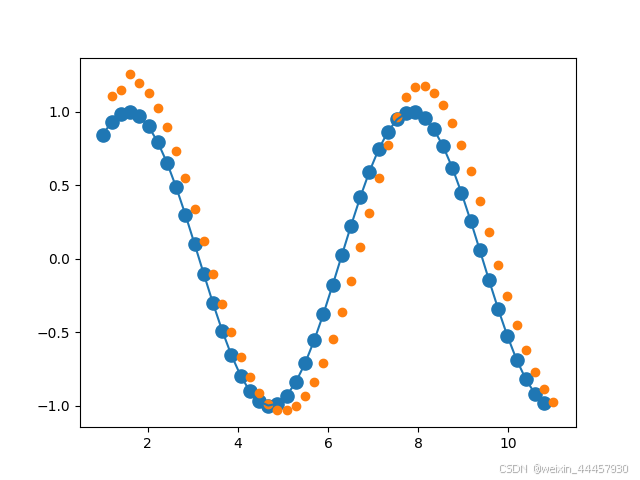
序列模型的使用示例
序列模型的使用示例 1 RNN原理1.1 序列模型的输入输出1.2 循环神经网络(RNN)1.3 RNN的公式表示2 数据的尺寸 3 PyTorch中查看RNN的参数4 PyTorch中实现RNN(1)RNN实例化(2)forward函数(3…...

对rust的全局变量使用drop方法
文章目录 rust处理全局变量的策略方法1:在main中自动Drop全局变量 参考 rust处理全局变量的策略 Rust 的静态变量不会在程序退出时自动调用 Drop,因为它们的生命周期与进程绑定。 use std::sync::OnceLock;struct GlobalData {content: String, }impl …...

Node.js教程入门第一课:环境安装
对于一个程序员来说,每学习一个新东西的时候,第一步基本上都是先进行环境的搭建! 从本章节开始让我们开始探索Node.js的世界吧! 什么是Node.js? 那么什么是Node.js呢?简单的说Node.js 就是运行在服务端的 JavaScript JavaScript…...
Visual Studio 使用 GitHub Copilot 扩展
🎀🎀🎀【AI辅助编程系列】🎀🎀🎀 Visual Studio 使用 GitHub Copilot 与 IntelliCode 辅助编码Visual Studio 安装和管理 GitHub CopilotVisual Studio 使用 GitHub Copilot 扩展Visual Studio 使用 GitHu…...

【Qualcomm】IPQ5018获取TR069 WiFi 接口Stats状态方法
IPQ5018 简介 IPQ5018 是高通(Qualcomm)公司推出的一款面向网络设备的系统级芯片(SoC)。它通常用于路由器、接入点和其他网络设备中,提供高性能的无线网络连接。以下是关于 IPQ5018 的一些关键特性和功能: 关键特性 高性能处理器 IPQ5018 集成了多核 CPU,通常是 ARM …...

数字营销咨询,照亮企业营销数字化每一步
在快消品领域,面对市场竞争日益激烈的现状,营销端的数字化升级已经成为企业生意增长的重要驱动力。 然而,鉴于营销端数字化建设的高昂成本及其广泛覆盖的业务范畴,企业在启动此类项目之前,通常会遭遇一系列挑战与顾虑&…...
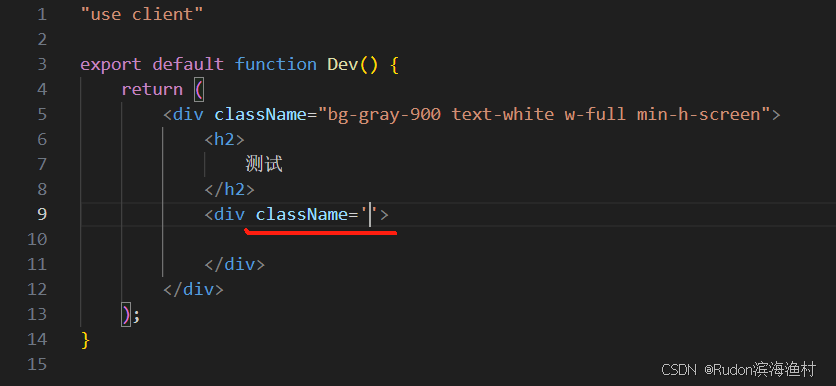
修改vscode中emmet中jsx和tsx语法中className的扩展符号从单引号到双引号 - HTML代码补全 - 单引号双引号
效果图 实现步骤 文件 > 首选项 > 设置搜索“”在settings.json中修改,增加 "emmet.syntaxProfiles": {"html": {"attr_quotes": "single"},"jsx": {"attr_quotes": "double","…...

【Cmake】
1 设置安装路径 -DCMAKE_INSTALL_PREFIX"安装路径"2 使用交叉编译 -DCMAKE_C_COMPILE"交叉编译器绝对路径"3 编译静态库 -DPAHO_BUILD_STARTTRUE...
Flutter 内嵌 unity3d for android
前言: 最近刚整完 unity3d hybridCLR 更新代码和资源,我们 趁热打铁 将 Unity3D 嵌入 Flutter 应用中。实现在 Flutter 使用 Unity3D, 可以做 小游戏 大游戏; 之前都是 内嵌 Webview 来实现的。虽然 CocosCreator 做出来的效果也不错…...
sqlite加密-QtCipherSqlitePlugin 上
1、下载并解压软件 https://download.csdn.net/download/notfindjob/90140129 2、编译(可支持Qt5.12编译) 3、安装插件...
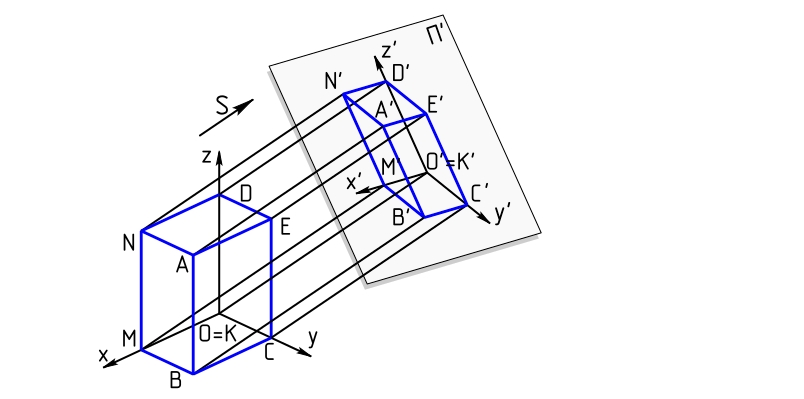
正交投影 (Orthographic Projection) 详解
正交投影 (Orthographic Projection) 详解 正交投影是一种将三维空间中的物体投影到二维平面上的方法,它在计算机图形学、建筑设计、工程绘图等领域中广泛应用。与透视投影不同,正交投影不会随着距离的变化而改变物体的大小,因此所有平行线在…...
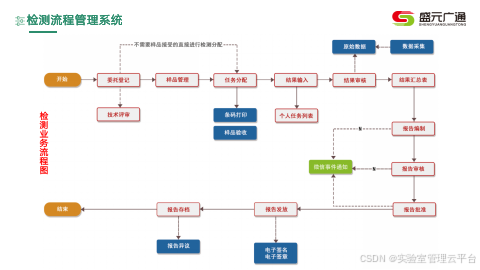
盛元广通畜牧与水产品检验技术研究所LIMS系统
一、系统概述 盛元广通畜牧与水产品检验技术研究所LIMS系统集成了检测流程管理、样品管理、仪器设备管理、质量控制、数据记录与分析、合规性管理等功能于一体,能够帮助实验室实现全流程的数字化管理。在水产、畜牧产品的质检实验室中,LIMS系统通过引入…...
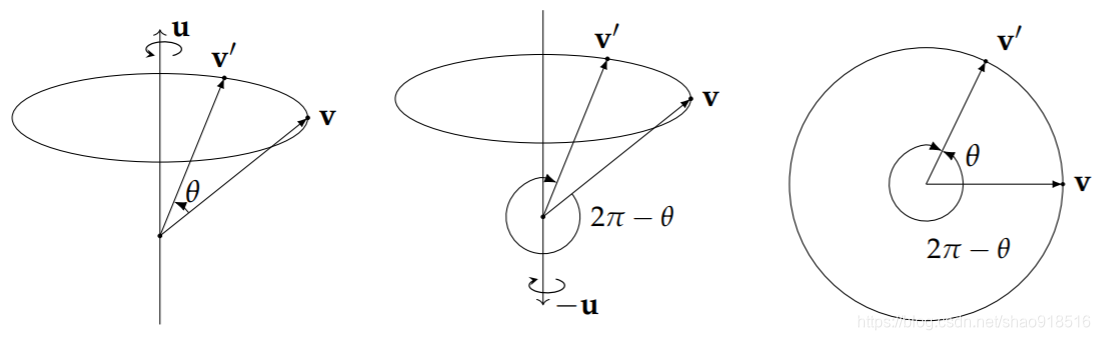
三维空间刚体运动4-1:四元数表示变换(各形式相互转换加代码——下篇)
三维空间刚体运动4-1:四元数表示变换(各形式相互转换加代码——下篇) 4. 四元数到其它旋转表示的相互转换4.1 旋转向量4.2 旋转矩阵4.3 欧拉角4.3.1 转换关系4.3.2 转换中的万象锁问题 5. 四元数的其他性质5.1 旋转的复合5.2 双倍覆盖5.3 指数…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
