素数回文数的个数
素数回文数的个数
- C语言代码
- C++ 代码
- Java代码
- Python代码
| 💐The Begin💐点点关注,收藏不迷路💐 |
求11到n之间(包括n),既是素数又是回文数的整数有多少个。
输入
一个大于11小于1000的整数n。
输出
11到n之间的素数回文数个数。
样例输入
23
样例输出
1
C语言代码
#include <stdio.h>
#include <stdbool.h>
// 判断一个数是否为素数
bool isPrime(int num) {
if (num < 2) return false;
for (int i = 2; i * i <= num; i++) { // 从2到根号num判断能否整除
if (num % i == 0) return false;
}
return true;
}
// 判断一个数是否为回文数
bool isPalindrome(int num) {
int original = num;
int reversed = 0;
while (num > 0) {
reversed = reversed * 10 + num % 10; // 取出个位数字并构造反转后的数
num /= 10;
}
return original == reversed; // 判断原数和反转后的数是否相等
}
int main() {
int n;
scanf(“%d”, &n);
int count = 0;
for (int i = 11; i <= n; i++) { // 遍历11到n的数
if (isPrime(i) && isPalindrome(i)) { // 如果既是素数又是回文数
count++;
}
}
printf(“%d\n”, count);
return 0;
}
C++ 代码
#include <iostream>
#include <cmath>
using namespace std;
// 判断一个数是否为素数
bool isPrime(int num) {
if (num < 2) return false;
for (int i = 2; i <= sqrt(num); i++) { // 从2到根号num判断能否整除
if (num % i == 0) return false;
}
return true;
}
// 判断一个数是否为回文数
bool isPalindrome(int num) {
int original = num;
int reversed = 0;
while (num > 0) {
reversed = reversed * 10 + num % 10; // 取出个位数字并构造反转后的数
num /= 10;
}
return original == reversed; // 判断原数和反转后的数是否相等
}
int main() {
int n;
cin >> n;
int count = 0;
for (int i = 11; i <= n; i++) { // 遍历11到n的数
if (isPrime(i) && isPalindrome(i)) { // 如果既是素数又是回文数
count++;
}
}
cout << count << endl;
return 0;
}
Java代码
import java.util.Scanner;
public class PrimeAndPalindrome {
// 判断一个数是否为素数
static boolean isPrime(int num) {
if (num < 2) return false;
for (int i = 2; i * i <= num; i++) { // 从2到根号num判断能否整除
if (num % i == 0) return false;
}
return true;
}
// 判断一个数是否为回文数
static boolean isPalindrome(int num) {
int original = num;
int reversed = 0;
while (num > 0) {
reversed = reversed * 10 + num % 10; // 取出个位数字并构造反转后的数
num /= 10;
}
return original == reversed; // 判断原数和反转后的数是否相等
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int count = 0;
for (int i = 11; i <= n; i++) { // 遍历11到n的数
if (isPrime(i) && isPalindrome(i)) { // 如果既是素数又是回文数
count++;
}
}
System.out.println(count);
}
}
Python代码
def is_prime(num):
if num < 2:
return False
for i in range(2, int(num ** 0.5) + 1): // 从2到根号num判断能否整除
if num % i == 0:
return False
return True
def is_palindrome(num):
return str(num) == str(num)[::-1] // 判断原数字字符串和反转后的字符串是否相等
n = int(input())
count = 0
for i in range(11, n + 1): // 遍历11到n的数
if is_prime(i) && is_palindrome(i): // 如果既是素数又是回文数
count += 1
print(count)

| 💐The End💐点点关注,收藏不迷路💐 |
相关文章:

素数回文数的个数
素数回文数的个数 C语言代码C 代码Java代码Python代码 💐The Begin💐点点关注,收藏不迷路💐 求11到n之间(包括n),既是素数又是回文数的整数有多少个。 输入 一个大于11小于1000的整数n。 输出…...

车辆重识别代码笔记12.18
1、实例归一化(Instance Normalization)和批量归一化(Batch Normalization) 实例归一化(Instance Normalization): 计算步骤: 对于每个输入样本,在每个通道上分别计算均…...

selenium 在已打开浏览器上继续调试
关闭浏览器,终端执行如下指令,--user-data-dir换成自己的User Data路径 chrome.exe --remote-debugging-port9222 --user-data-dir"C:\Users\xxx\AppData\Local\Google\Chrome\User Data" 会打开浏览器,打开百度,如下状…...

Sentry日志管理thinkphp8 tp8 sentry9 sentry8 php8.x配置步骤, tp8自定义异常处理类使用方法
tp8的默认使用的就是composer来管理第三方包, 所以直接使用 composer 来安装 sentry9 即可. 同时tp8和tp5的配置方式不太一样, 这里我们直接使用自定义异常类来处理Sentry的异常. 1. 安装 sentry9 包 # 安装 sentry9 包 composer require "tekintian/sentry9-php" …...

【经验分享】容器云搭建的知识点
最近忙于备考没关注,有次点进某小黄鱼发现首页出现了我的笔记还被人收费了 虽然我也卖了一些资源,但我以交流、交换为主,笔记都是免费给别人看的 由于当时刚刚接触写的并不成熟,为了避免更多人花没必要的钱,所以决定公…...

Java对集合的操作方法
1. 数组转集合 //数组转集合 String[] split quickRechargeAmount.split(","); List<String> stringList Stream.of(split).collect(Collectors.toList()); 2. 对List集合数据内容进行分组 //对List集合数据内容进行分组 Map<String, List<LiveAppGi…...

FreeRTOS--基础知识
FreeRTOS基础知识 裸机与RTOS的特点: 裸机: 裸机又称为前后台系统,前台系统指的是中断服务函数,后台系统指的是大循环,即应用程序。 1、实时性差:应用程序轮流执行 2、delay:空等待ÿ…...

Node的学习以及学习通过Node书写接口并简单操作数据库
Node的学习 Node的基础上述是关于Node的一些基础,总结的还行; 利用Node书写接口并操作数据库 1. 初始化项目 创建新的项目文件夹,并初始化 package.json mkdir my-backend cd my-backend npm init -y2. 安装必要的依赖 安装Express.js&…...

【Linux探索学习】第二十二弹——用户缓冲区:深入解析操作系统中数据交互时的缓冲区机制
Linux学习笔记: https://blog.csdn.net/2301_80220607/category_12805278.html?spm1001.2014.3001.5482 前言: 前面两章我们已经讲了一些文件操作和文件重定向问题,以及一些相关的知识点,比如文件在内存中的存储位置࿰…...

Cesium-(Primitive)-(CylinderOutlineGeometry)
CylinderOutlineGeometry 以下是 CylinderOutlineGeometry 类的构造函数属性,以表格形式展示: 属性名类型默认值描述lengthnumber圆柱体的长度。topRadiusnumber圆柱体顶部的半径。bottomRadiusnumber圆柱体底部的半径。slicesnumber128可选,圆柱体周长的边数。numberOfVert…...

【ETCD】【源码阅读】深入分析 storeTxnWrite.Put方法源码
该方法是 storeTxnWrite 类型中的核心方法,负责将键值对存储到数据库,同时处理键的元数据(如版本、修订号、租约)并管理租约关联。 目录 一、完整代码二、方法详解方法签名1. 计算修订号并初始化变量2. 检查键是否已存在3. 生成索…...

MySQL技术:深入理解索引与优化
MySQL是一个广泛使用的开源关系型数据库管理系统。它以其高性能、可靠性和易用性而闻名。在数据库操作中,查询优化是一个非常重要的环节,而索引是实现查询优化的关键技术之一。本文将深入探讨MySQL中的索引原理、类型以及如何优化索引以提高数据库性能。…...
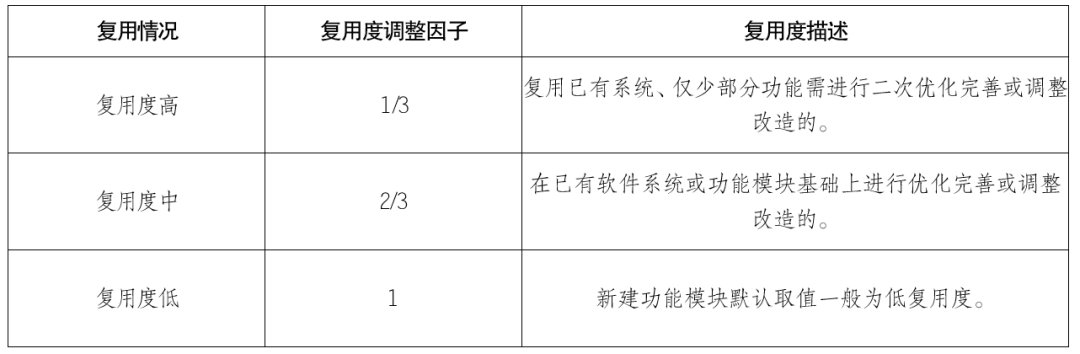
【广东-东莞】《东莞市政府投资信息化项目造价指南》-省市费用标准解读系列26
2023年6月27日,东莞市发展和改革局发布《东莞市政府投资信息化项目造价指南(试行)》,此指南由东莞市政府投资项目评审中心编制,指南旨在完善东莞市为规范政府投资信息化项目造价计费方式,高质量、高效率推进…...

8、基于SpringBoot的房屋租赁系统
摘 要 社会的发展和科学技术的进步,互联网技术越来越受欢迎。网络计算机的生活方式逐渐受到广大人民群众的喜爱,也逐渐进入了每个用户的使用。互联网具有便利性,速度快,效率高,成本低等优点。 因此,构建符…...

SLM510A系列——24V,15到150mA单通道可调电流线性恒流LED驱动芯片
SLM510A 系列产品是单通道、高精度、可调电流线性恒流源的 LED 驱动芯片,在各种 LED 照明产品中非常简单易用。其在宽电压输入范围内,能保证极高的输出电流精度,从而在大面积的光源照明中,都能让 LED 照明亮度保持均匀一致。 由于…...

深度学习试题及答案解析(一)
1. 一幅256*256的图像,若灰度级数为16,则存储它所需的比特数是() 2. 在深度学习中,涉及大量的矩阵相乘,现在需要计算三个稠密矩阵A,B,C的乘积ABC,假设三个矩阵的尺寸分别为m∗n&…...

【钉钉群聊机器人定时发送消息功能实现】
Java实现 钉钉群聊机器人定时发送消息功能 钉钉群聊准备工作钉钉发起群聊创建项目群打开钉钉群聊设置打开机器人管理选择Webhook机器人添加机器人安全设置保存Webhook地址(重点是token) 项目代码实现添加依赖启动类添加定时任务启动扫描编写调度任务定义…...

uni-app多环境配置动态修改
前言 这篇文章主要介绍uniapp在Hbuilderx 中,通过工程化,区分不同环境、动态修改小程序appid以及自定义条件编译,解决代码发布和运行时手动切换问题。 背景 当我们使用uniapp开发同一个项目发布不同的环境二级路径不同时,这时候…...

verilog代码连线集成工具的实践
目录 引言 代码解析 解析器的需求 数据结构 基础class 集合class: 界面 模块例化里界面 连线界面 连线界面示例 消息传递 引言 工作中经常需要开发很多自动化的脚本或者小工具来提升开发效率。在没有读《Cad Frameworks: Principles And Architecture》…...

【深入STL:C++容器与算法】深度解析string类的使用
文章目录 1️⃣什么是stringstring的设计以及编码问题 2️⃣string的重要接口💫💫一、string的初始化二、string的赋值三、string的长度四、string元素获取1. char& at(size_t pos)2. operaotr []3. front和back 五、迭代器1. 什么是迭代器2. 范围fo…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
