使用 rbenv 切换 Ruby 版本
1. 查看当前 Ruby 版本
首先,查看当前系统中安装的 Ruby 版本:
ruby -v
如果你已经安装了 rbenv,可以列出通过 rbenv 安装的 Ruby 版本:
rbenv versions
2. 安装 Ruby 版本
如果你想安装新的 Ruby 版本,使用以下命令:
rbenv install <版本号>
例如,安装 Ruby 3.1.0:
rbenv install 3.1.0
如果你不知道有哪些可用版本,可以通过以下命令查看:
rbenv install --list
3. 切换 Ruby 版本
有两种方式切换 Ruby 版本:
-
全局切换:
全局切换会影响系统中所有的终端会话。你可以通过以下命令切换 Ruby 版本:rbenv global <版本号>例如,设置全局 Ruby 版本为 3.1.0:
rbenv global 3.1.0 -
局部切换:
局部切换是针对当前目录的。如果你只想在某个项目中使用特定版本的 Ruby,可以在该项目的目录中设置局部版本:rbenv local <版本号>例如,设置当前目录的 Ruby 版本为 2.7.6:
rbenv local 2.7.6
4. 查看当前使用的 Ruby 版本
切换完版本后,可以使用以下命令查看当前正在使用的 Ruby 版本:
rbenv version
5. 重新初始化环境
每次切换 Ruby 版本后,记得重新加载你的 shell 配置文件:
source ~/.zshrc # 如果你使用 zsh
# 或者
source ~/.bash_profile # 如果你使用 bash
通过这些步骤,你就可以使用 rbenv 来管理和切换不同的 Ruby 版本。
相关文章:

使用 rbenv 切换 Ruby 版本
1. 查看当前 Ruby 版本 首先,查看当前系统中安装的 Ruby 版本: ruby -v如果你已经安装了 rbenv,可以列出通过 rbenv 安装的 Ruby 版本: rbenv versions2. 安装 Ruby 版本 如果你想安装新的 Ruby 版本,使用以下命令…...
C语言(结构体练习)
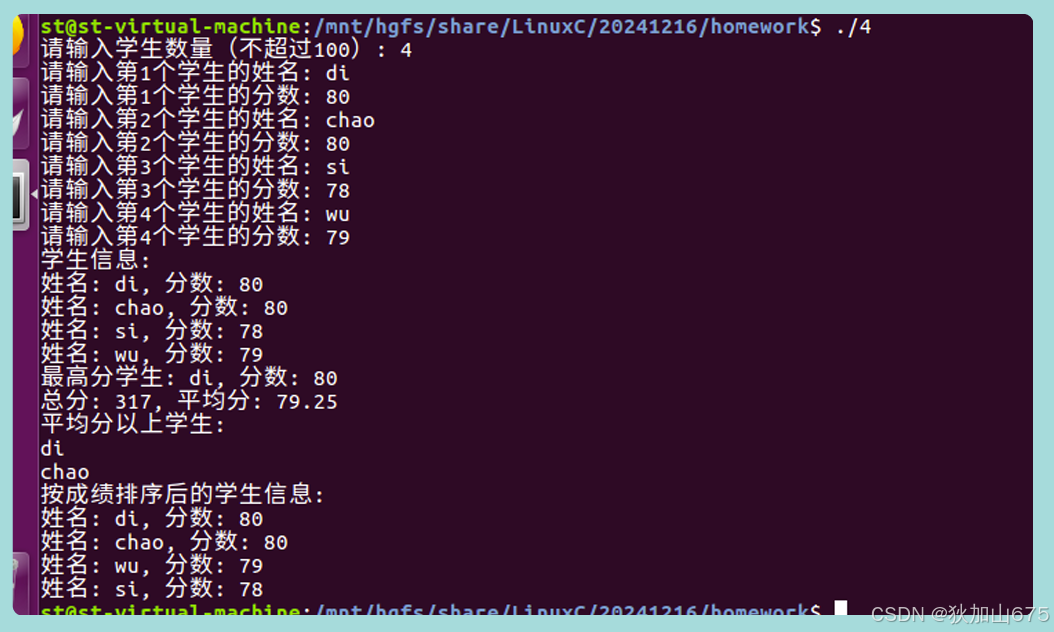
设计一个结构体,存放一个学员信息并显示,存放两个学员信息,算他们的平均分。 #include <stdio.h> #include <string.h>// 定义结构体 typedef struct {char name[50];float score; } Student;// 函数声明 void display(Student student); f…...

你了解网络层的 ICMP 吗?
你了解网络层的 ICMP 吗? 一. 什么是 ICMP二. ICMP 的工作原理三. ICMP 的结构四. ICMP 的常见应用五. ICMP 的局限性与安全性六. 总结 前言 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神…...
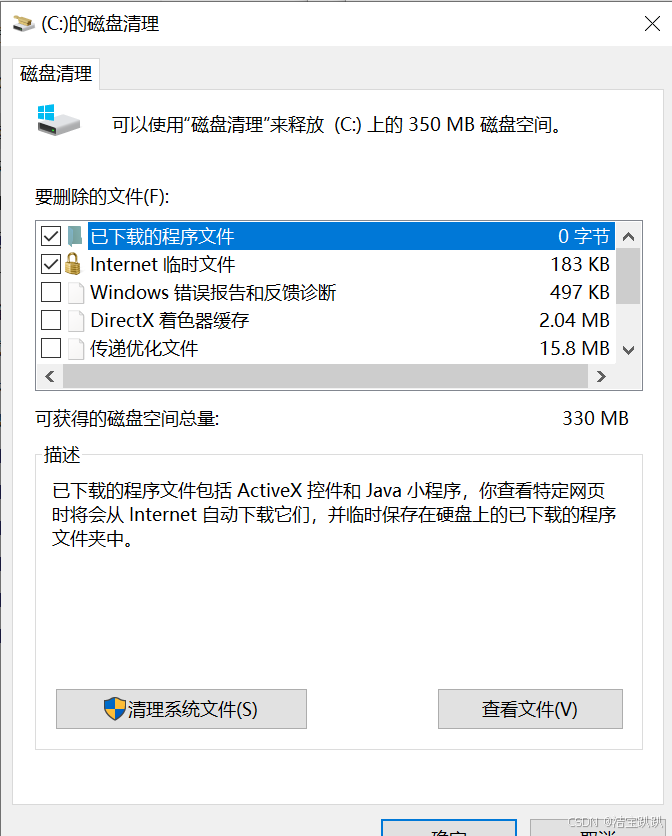
清理C盘小记
突然C盘就爆满了,想当初还是给他预留了120G的空间,感觉到现在也不够用了,担心出现死机的情况就赶紧进行了清理。有一说一,清理回收站是真的有用。 参考:C盘清理指南,清理出30G起,超详细总结&am…...

Excel中如何消除“长短款”
函数微调可以可以实施,简单且易于操作的气球🎈涨缩更妙。 (笔记模板由python脚本于2024年12月17日 06:19:13创建,本篇笔记适合用Excel操作数据的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Fre…...

超越 RAG 基础:AI 应用的高级策略
作者:来自 Elastic Elastic Platform Team 我们最近与 Cohere 举办的虚拟活动深入探讨了检索增强生成 (retrieval augmented generation - RAG) 的世界,重点讨论了在概念验证阶段之后构建 RAG 应用程序的关键注意事项。我们的演讲者是 Elastic 的首席解…...

[shader]【图形渲染】【unity】【游戏开发】 Shader数学基础2-认识点和矢量
在计算机图形学和Shader编程中,点和矢量是两种常见且基础的数学对象。它们在空间中的作用和性质是理解图形渲染的关键。本篇文章将深入探讨点(Point)和矢量(Vector)的定义、特性以及它们之间的关系。 1. 点(Point)的定义 在数学和计算机图形学中,**点(Point)**用于…...

微软开源Python Markdown转换工具
分享一个microsoft开源的Python工具——markitdown,轻松将各类文件转换为Markdown格式。 markitdown支持的文件格式 PDF(.pdf)PowerPoint(.pptx)Word(.docx)Excel(.xlsx)图片(支持EXIF元数据和OCR识别)音频(支持EXIF元数据和语音转录)HTML(包括对Wikipedia...

安装与配置MongoDB 6.0以支持远程连接
安装与配置MongoDB 6.0以支持远程连接 目录 安装curl工具下载并导入MongoDB 6.0 PGP密钥向APT导入MongoDB 6.0版软件包的资源链接安装MongoDB依赖libssl1.1安装MongoDB启动并检查MongoDB服务状态进入MongoDB Shell交互式执行环境设置MongoDB开机自启配置MongoDB允许远程连接 …...

零衍门户国际化:助力拓展全球视野
概述 零衍系统管理平台统一门户管理,支持门户看板灵活配置,同时提供场景化的门户模板,丰富的门户组件,可协助用户快速搭建企业专属门户。 随着零衍产品的不断成熟,国际化需求日益增多,客户期望零衍门户可…...

mysql免安装版配置教程
一、将压缩包解压至你想要放置的文件夹中,注意:绝对路径中要避免出现中文 二、在解压目录下新建my.ini文件,已经有的就直接覆盖 my.ini文件内容 [mysqld] # 设置3306端口 port3306 # 设置mysql的安装目录 basedirD:\\tools\\mysql-8.1.0-win…...

kafka的处理的一些问题 消费延迟
kafka的处理的一些问题 消费者客户端不但没有背压而且内存充足,但产生的消费延迟越来越大在Kafka的Leader副本宕机时 消费者客户端不但没有背压而且内存充足,但产生的消费延迟越来越大 比如我们这个kakfa集群一共有3个Broker节点 TOp1有5个分区…...

旅游创业,千益畅行,开启新的旅游模式!
在当今旅游市场蓬勃发展的时代,旅游卡项目如一颗新星闪耀登场,而千益畅行旅游卡服务更是其中的佼佼者,为广大旅游爱好者带来了全新的旅游体验与机遇。 一、旅游卡项目是如何运作的呢? 千益畅行旅游卡服务的运作模式犹如一部精心…...

集成自然语言理解服务,让应用 “听得懂人话”
如今,应用程序智能化已成趋势,开发者想要实现智能化,那么首先需要赋予应用理解自然语言的能力,使其能够准确地听懂人话,进而响应用户需求,并提供一系列智能化服务。比如用户语音控制应用程序帮忙订票&#…...

利用notepad++删除特定关键字所在的行
1、按组合键Ctrl H,查找模式选择 ‘正则表达式’,不选 ‘.匹配新行’ 2、查找目标输入 : ^.*关键字.*\r\n (不保留空行) ^.*关键字.*$ (保留空行)3、替换为:(空) 配置界面参考下图: …...

[HNOI2002] 营业额统计 STL - set集合
文章目录 [HNOI2002] 营业额统计题目描述样例输入 #1样例输出 #1 提示题解相关知识点set [HNOI2002] 营业额统计 STL - set解题 题目描述 Tiger 最近被公司升任为营业部经理,他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。 Tiger 拿出…...
)
fastAPI接口(普通流式响应和大模型流式响应)
1. 流式输出和非流失输出: 大模型的流式输出(Streaming Output)和非流式输出(Non-streaming Output)是指在生成文本或其他输出时,如何将结果返回给用户或下游系统。 流式输出 (Streaming Output)…...

Linux系统安装node.js
一、node官网下载想要的node版本 https://nodejs.org/en/download/package-manager 二、将tar.xz文件解压 tar -xvf node-vxxx.tar.xz 三、改文件夹的名字,改成nodejs mv node-xxx nodejs 四、复制nodejs文件,并上传到linux 服务器 /usr/local 目录下…...

《解决两道有趣的编程问题:交替数字和与简单回文》
在编程的世界里,算法和逻辑的挑战无处不在。今天,我们将用 Python 来解决两道有趣的编程问题,分别是计算交替数字和以及生成简单回文。 一、交替数字和(Alternating Sum of Numbers) 1. 问题描述 给定一系列整数&am…...

2412d,d的8月会议
原文 总结 替换D的逃逸分析 Rikki说,他一个月前曾与Dennis讨论过简化D的逃逸分析,但没有结果.在BeerConf上,他再次提起了它,Dennis说他一直在考虑它. Rikki也与Walter谈过这件事,Walter曾说过DIP1000并没有完全如期工作,且有点太复杂了. 因此,Rikki想讨论按D逃逸分析方法替…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
