数据结构_平衡二叉树
结点类
构造函数分为有参和无参,相同点都是初始化树高为1
class Node
{
public:int data; // 用于输出int val; // 数据域,用于排序int height; // 树高Node* left;Node* right;Node();Node(int v, int d);static int max(int a, int b);
};Node::Node()
{data = -1;val = -1;height = 1;left = nullptr;right = nullptr;
}Node::Node(int v, int d)
{data = d;val = v;height = 1;left = nullptr;right = nullptr;
}int Node::max(int a, int b)
{return (a > b) ? a : b;
}
获取平衡因子
左子树树高减去右子树树高
int getB(Node* n)
{int leftHeight = (n->left) ? n->left->height : 0;int rightHeight = (n->right) ? n->right->height : 0;return leftHeight - rightHeight;
}
解决RR型不平衡,左旋
- 新的根节点为当前根节点的右子树
- 当前根结点的右子树的左子树,改变后为当前根结点的右子树(如果存在的话)
- 当前根节点变为新的根节点的左子树
- 最后要更新改变前后两个新旧根节点的树高,都等于1 + 左右子树的树高比较后的最大值
Node* leftRoatte(Node* n) // 左旋(RR)
{Node* newroot = n->right;Node* T2 = newroot->left;newroot->left = n;n->right = T2;// 更新树高n->height = 1 + Node::max(n->left ? n->left->height : 0, n->right ? n->right->height : 0);newroot->height = 1 + Node::max(newroot->left ? newroot->left->height : 0, newroot->right ? newroot->right->height : 0);return newroot;
}
解决LL型不平衡,右旋
实现方法与RR型大差不差
Node* rightRoatte(Node* n) // 右旋(LL)
{Node* newroot = n->left;Node* T2 = newroot->right;newroot->right = n;n->left = T2;// 更新树高n->height = 1 + Node::max(n->left ? n->left->height : 0, n->right ? n->right->height : 0);newroot->height = 1 + Node::max(newroot->left ? newroot->left->height : 0, newroot->right ? newroot->right->height : 0);return newroot;
}
结点的插入函数
- 如果传入进来的为空结点,即当前结点无数据,则需要把传入进来的用于排序和输出的值作为参数构造一个新的结点,然后返回出去
- 否则,则进行判断,判断当前结点的关键值与传入进来的关键值进行判断,如果传入进来的值比当前结点的值要小,则表示需要插入进当前结点的左子树,递归调用插入函数,参数是当前结点的左子树,关键值和数据域,返回后的结点赋值给当前结点的左子树
- 如果传入进来的关键值大于当前结点的关键值,则插入右子树,方法类似
- 如果当前结点的关键值等于传入进来的关键值,则表示这个值已经在树中存在,不需要插入,则直接将当前结点的返回出去
- 执行完插入结点的操作后,需要更新树高,方法一样
- 还需要更新平衡因子,因为当插入一个结点后,需要判断此时是否为平衡二叉树,根据不同结点的平衡因子进行不同的调整
- 首先获取当前根结点的平衡因子,如果当前根节点的平衡因子大于1,且当前结点的左子树根结点大于0,即他还有左子树,则为LL型,则调用右旋函数,返回调用后的结果
- 如果当前根节点的的平衡因子大于1,且当前根节点的左子树的根节点小于0,则其有右子树,为LR型,LR型首先要将当前结点的左子树为参数进行左旋,然后再将当前结点进行右旋,返回调用后的结果
- 其他两种情况类似
- 最后返回当前结点
Node* Insert(Node* now, int key, int data)
{if (now == nullptr){return new Node(key, data);}if (key < now->val){now->left = Insert(now->left, key, data);}else if (key > now->val){now->right = Insert(now->right, key, data);}else{return now; // Key already exists, don't insert duplicate}// 更新树高now->height = 1 + Node::max(now->left ? now->left->height : 0, now->right ? now->right->height : 0);// 获取当前结点的平衡因子int balance = getB(now);if (balance > 1 && getB(now->left) >= 0) // LL{return rightRoatte(now);}else if (balance > 1 && getB(now->left) < 0) // LR{now->left = leftRoatte(now->left);return rightRoatte(now);}else if (balance < -1 && getB(now->right) <= 0) // RR{return leftRoatte(now);}else if (balance < -1 && getB(now->right) > 0) // RL{now->right = rightRoatte(now->right);return leftRoatte(now);}return now;
}
相关文章:

数据结构_平衡二叉树
结点类 构造函数分为有参和无参,相同点都是初始化树高为1 class Node { public:int data; // 用于输出int val; // 数据域,用于排序int height; // 树高Node* left;Node* right;Node();Node(int v, int d);static int max(int a, int b); };Node::N…...

C++对象的赋值与复制复制构造函数(指针数据成员)
一、对象的赋值 同类对象之间可以相互赋值,对象赋值的一般形式:对象名2 对象名1; 原理是,赋值运算符的重载。仅赋值,因此赋值前,需要先定义并初始化对象2。 对象的赋值针对指对象中所有数据成员的值; 对…...

Coding Caprice - monotonic stack2
42. 接雨水 class Solution { public:int trap(vector<int>& height) {stack<int> sh;int out 0;for(int i0; i<height.size(); i){while(!sh.empty() && height[sh.top()]<height[i]){int bo height[sh.top()];sh.pop();if(sh.empty()){brea…...
)
Spring Mvc面试题(常见)
1 Spring MVC的执行流程 用户发起请求,请求先被Servlet拦截以后,转发给SpringMVC框架SpringMVC 里面的DispatcherServlet(核心控制器) 接收到请求,并转发给HandlerMappingHandlerMapping负责解析请求,根据请求信息和配置信息找到匹配的Controller类(当这里有配置拦截器,会…...

opencv # Sobel算子、Laplacian算子、Canny边缘检测、findContours、drawContours绘制轮廓、外接矩形
一、Sobel算子 案例图片 cv2.Sobel(src, ddepth, dx, dy, ksize3, scale1, delta0, borderTypeNone) 功能:用于计算图像梯度(gradient)的函数 参数: src: 输入图像,它应该是灰度图像。 ddepth: 输出图像的所需深度&am…...

Neo4j插入数据逐级提升速度4倍又4倍
语雀版:https://www.yuque.com/xw76/back/dtukgqfkfwg1d6yo 目录 背景介绍初始方案Node()创建事务批量提交记录Node是否存在生成Cypher语句执行数据库参数优化切换成85k个三元组测试建索引(很显著!!!)MATCH…...

C++特殊类设计(单例模式等)
目录 引言 1.请设计一个类,不能被拷贝 2. 请设计一个类,只能在堆上创建对象 为什么设置实例的方法为静态成员呢 3. 请设计一个类,只能在栈上创建对象 4. 请设计一个类,不能被继承 5. 请设计一个类,只能创建一个对…...

J8学习打卡笔记
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 Inception v1算法实战与解析 导入数据数据预处理划分数据集搭建模型训练模型正式训练结果可视化详细网络结构图个人总结 import os, PIL, random, pathlib imp…...
)
前端学习-操作元素内容(二十二)
目录 前言 目标 对象.innerText 属性 对象.innerHTML属性 案例 年会抽奖 需求 方法一 方法二 总结 前言 曾经沧海难为水,除却巫山不是云。 目标 能够修改元素的文本更换内容 DOM对象都是根据标签生成的,所以操作标签,本质上就是操作DOM对象,…...

【踩坑】pip离线+在线在虚拟环境中安装指定版本cudnn攻略
pip离线在线在虚拟环境中安装指定版本cudnn攻略 在线安装离线安装Windows环境:Linux环境: 清华源官方帮助文档 https://mirrors.tuna.tsinghua.edu.cn/help/pypi/ 标题的离线的意思是先下载whl文件再安装到虚拟环境,在线的意思是直接在当前虚…...

golang操作sqlite3加速本地结构化数据查询
目录 摘要Sqlite3SQLite 命令SQLite 语法SQLite 数据类型列亲和类型——优先选择机制 SQLite 创建数据库SQLite 附加数据库SQLite 分离数据库 SQLite 创建表SQLite 删除表 SQLite Insert 语句SQLite Select 语句SQLite 运算符SQLite 算术运算符SQLite 比较运算符SQLite 逻辑运算…...
与流式响应)
vllm加速(以Qwen2.5-7B-instruction为例)与流式响应
1. vllm介绍 什么是vllm? vLLM 是一个高性能的大型语言模型推理引擎,采用创新的内存管理和执行架构,显著提升了大模型推理的速度和效率。它支持高度并发的请求处理,能够同时服务数千名用户,并且兼容多种深度学习框架,…...

WordPress弹窗公告插件-ts小陈
使用效果 使用后网站所有页面弹出窗口 插件特色功能 设置弹窗公告样式:这款插件可展示弹窗样式公告,用户点击完之后不再弹出,不会频繁打扰用户。可设置弹窗中间的logo图:这款插件针对公告图片进行独立设置,你可以在设…...

【ELK】容器化部署Elasticsearch1.14.3集群【亲测可用】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. 部署1.1 单节点1.2 新节点加入集群1.3 docker-compose部署集群 1. 部署 按照官网流程进行部署 使用 Docker 安装 Elasticsearch |Elasticsearch 指南 [8.14] |…...

[SAP ABAP] ALV状态栏GUI STATUS的快速创建
使用事务码SE38进入到指定程序,点击"显示对象列表"按钮 鼠标右键,选择"GUI状态" 弹出【创建状态】窗口,填写状态以及短文本描述以后,点击按钮 点击"调整模板",复制已有程序的状态栏 填…...

【Linux】NET9运行时移植到低版本GLIBC的Linux纯内核板卡上
背景介绍 自制了一块Linux板卡(基于全志T113i) 厂家给的SDK和根文件系统能够提供的GLIBC的版本比较低 V2.25/GCC 7.3.1 这个版本是无法运行dotnet以及dotnet生成的AOT应用的 我用另一块同Cortex-A7的板子运行dotnet的报错 版本不够,运行不了 而我的板子是根本就识…...
)
深入浅出支持向量机(SVM)
1. 引言 支持向量机(SVM, Support Vector Machine)是一种常见的监督学习算法,广泛应用于分类、回归和异常检测等任务。自1990年代初期由Vapnik等人提出以来,SVM已成为机器学习领域的核心方法之一,尤其在模式识别、文本…...

Vue脚手架相关记录
脚手架 安装与配置 安装node node -> 16.20.2 切换淘宝镜像 npm install -g cnpm -registryhttp://registry.npm.taobao.orgnpm config set registry http://registry.npm.taobao.org/使用了第二个,下一步才有用 安装vue npm install -g vue/clivscode中不给运行vue解…...

基于Docker的Minio分布式集群实践
目录 1. 说明 2. 配置表 3. 步骤 3.1 放行服务端口 3.2 docker-compose 编排 4. 入口反向代理与负载均衡配置 4.1 api入口 4.2 管理入口 5. 用例 6. 参考 1. 说明 以多节点的Docker容器方式实现minio存储集群,并配以nginx反向代理及负载均衡作为访问入口。…...

Scala 的迭代器
迭代器定义:迭代器不是一种集合,它是一种用于访问集合的方法。 迭代器需要通过集合对应的迭代器调用迭代器的方法来访问。 支持函数式编程风格,便于链式操作。 创建一个迭代器,相关代码如下: object Test {def mai…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...
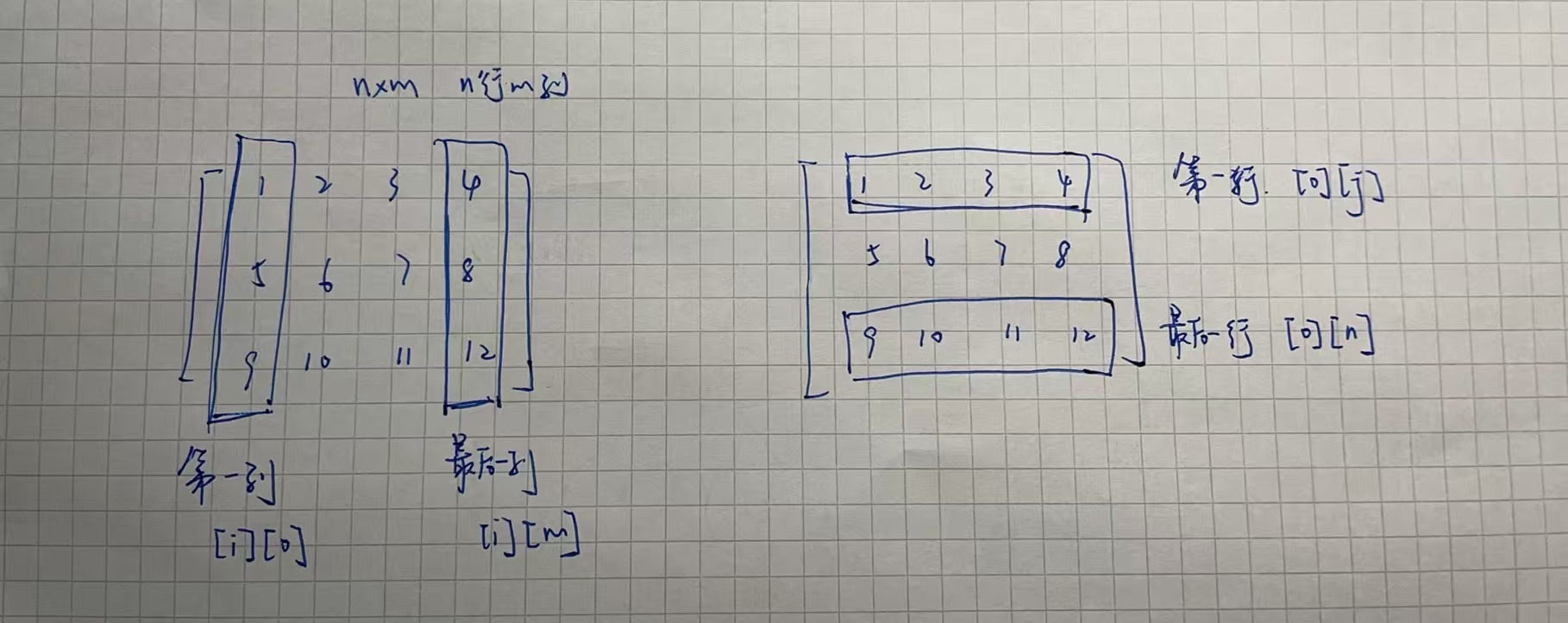
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...
