【排序算法】——选择排序
前言
排序(Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个关键字有序的序列。所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
排序算法,就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。
简介
所谓排序算法,即通过特定的算法因式将一组或多组数据按照既定模式进行重新排序。这种新序列遵循着一定的规则,体现出一定的规律,因此,经处理后的数据便于筛选和计算,大大提高了计算效率。对于一个排序算法的优劣,我们需要从它的时间复杂度、空间复杂度和稳定性三个方面来考虑。什么叫稳定性呢?即当两个相同的元素同时出现于某个序列之中,则经过一定的排序算法之后,两者在排序前后的相对位置不发生变化。换言之,即便是两个完全相同的元素,它们在排序过程中也是各有区别的。
本篇文章讲述的是排序算法中的选择排序,其中包含了两种排序算法,分别是直接选择排序和堆排序,下面将会一一为大家详细介绍。(用升序进行讲解)
基本思想
选择排序算法的基本思想是为每一个位置选择当前最小的元素。
1.直接选择排序
下面我们首先来看一看直接选择排序算法的动图演示:

看了上图我们可以得知,直接选择排序算法是首先从第1个位置开始对全部元素进行选择,选出全部元素中最小的给该位置,再对第2个位置进行选择,在剩余元素中选择最小的给该位置即可;以此类推,重复进行“最小元素”的选择,直至完成第(n-1)个位置的元素选择,则第n个位置就只剩唯一的最大元素,此时不需再进行选择。
直接选择排序算法的思路以及代码都比较简单,有了上述讲解相信大家都已经对其了解了。
2.堆排序
直接选择排序是选择排序的一种,但是其时间复杂度很高,在实际应用中效率非常低下,那有没有其他的效率高的选择排序呢?答案当然是有的,那就是堆排序(Heapsort),堆排序主要借助了我们的数据结构--堆来实现。(若是对堆不了解的可以去阅读我的另一篇文章数据结构--堆)。
当一个堆是大根堆的时候我们知道堆顶元素永远是整个堆中最大的元素,因此每次取堆顶我们都会得到一个最大值(降序则需要用小根堆),这刚好与我们选择排序算法的基本思想相同。下面我将同图画来给大家进行演示:

此时堆顶元素是数组中最大的元素,将其与最后一个元素交换位置,并对堆进行调整。

此时对于 9 这个元素我们可以理解为已经把它从该堆中删除了,此时堆中只剩下4个元素,重复此操作即可完成排序,大家可以根据下方的代码具体了解。
代码实现
1.直接插入排序
先看原始代码:
void Select_sort(vector<int>& a)
{int n = a.size();//对于直接选择排序来说,只需要进行n - 1次循环即可for (int i = 0; i < n - 1; i++){int minpos = i;//从i位置开始,遍历其后面的数组,找到最小值for (int j = i + 1; j < n; j++){if (a[j] < a[minpos]){minpos = j;}}//将最小值所处的位置与i位置的值进行交换即可swap(a[i], a[minpos]);}
}解析:两次循环即可完成,第一层循环控制需要排序的位置,第二次循环寻找该位置后的最小值。
对于直接选择排序,我们有一种优化办法,可以使其的时间效率增加一倍,虽说时间复杂度是相同的,杯水车薪,但也是一种思路。
具体思路:
第一层循环我们从数组的两端开始遍历;
第二次循环我们同时寻找其中间的最大值和最小值。
代码如下:
void Select_sort(vector<int>& a)
{int n = a.size();//数组大小为奇数,最后会处于left == right;当数组大小为偶数时,最后会处于left > right//因此结束条件为left < rightfor (int left = 0, right = n - 1; left < right; left++, right--){int minpos = left;int maxpos = left;//从left位置遍历其后面到right位置之前的数组,找到最小值和最大值for (int i = left + 1; i < right; i++){if (a[i] < a[minpos]){minpos = i;}if (a[i] > a[maxpos]){maxpos = i;}}//此时在交换元素时需要注意一个细节://当我们将a[right]与a[maxpos]交换时,maxpos位置上之前可能是left的位置,这样在之后的交换会出现问题,因此我们需要进行判断接下来的交换是否还要进行swap(a[right], a[maxpos]);if (a[minpos] < a[left]){swap(a[left], a[minpos]);}}
}对于优化后的直接选择排序在最后的交换步骤时的细节需要大家额外注意,大家可以自己用一个倒序数组亲自体验一下,以便有更深刻的体会。
2.堆排序
先看代码:
//向下调整算法
void AdjustDown(vector<int>& a, int parent, int end)
{int child = parent * 2 + 1;while (child < end){if (child + 1 < end && a[child] < a[child + 1]){child++;}if (a[child] > a[parent]){swap(a[child], a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void Heap_sort(vector<int>& a)
{int n = a.size();//首先进行建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, i, n);}//进行排序for (int i = n - 1; i > 0; i--){swap(a[0], a[i]);AdjustDown(a, 0, i);}
}对于堆排序来说,比较重要的地方是当我们在进行排序时,一定要注意当每一次交换完元素后,堆中的数据就会减少一个,因此当我们在自己写向下调整算法时,一定要注意此时堆中的数据个数,不然就会出现错误。
注:对于建堆和向下调整算法不了解的朋友可以先去看一看数据结构--堆,里面有较为详细的介绍。
总结
1.时空复杂度
经过分析我们可以得到直接选择排序的时间复杂度和空间复杂度,两层for循环以及常数个变量,因此
直接选择排序:
时间复杂度:O(N ^ 2)
空间复杂度:O(1)
对于堆排序来说,时间复杂度由建堆操作和排序操作决定,具体的计算过程较为复杂,感兴趣的可以自己搜索一下,这里不再赘述。因此
堆排序:
时间复杂度:O(NlogN)
空间复杂度:O(1)
堆排序算法的总体时间复杂度是 O(n log n),这是因为建堆之后,还需要进行 n-1 次的排序操作,每次排序操作的时间复杂度是 O(log n)。但是,建堆本身的时间复杂度是线性的,这使得堆排序在某些情况下比其他 O(n log n) 排序算法更高效。
2.稳定性
在排序算法中,我们不光要关注算法的时空复杂度,还在看看算法的稳定性,什么是稳定性呢?
稳定性是假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
简单分析我们可以知道选择排序算法是不稳定的。举例说明:序列58539.我们知道第一遍选择第1个元素“5”会和元素“3”交换,那么原序列中的两个相同元素“5”之间的前后相对顺序就发生了改变。因此,我们说选择排序不是稳定的排序算法,它在计算过程中会破坏稳定性。(对于直接选择排序以及堆排序都是如此)
直接选择排序: 不稳定
堆排序: 不稳定
尾声
若有纰漏或不足之处欢迎大家在评论区留言或者私信,同时也欢迎各位一起探讨学习。感谢您的观看!
相关文章:

【排序算法】——选择排序
前言 排序(Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个关键字有序的序列。所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小&#x…...

第十五章 Linux Shell 编程
15.1 Shell 变量 了解:Shell的功能 了解:Shell的种类 了解:Shell的调用 了解:Shell变量的概念 了解:Shell变量的定义 了解:Shell数组变量 了解:Shell内置变量 了解:双引号 和…...
)
【c++笔试强训】(第三十八篇)
目录 不相邻取数(动态规划-线性dp) 题目解析 讲解算法原理 编写代码 空调遥控(⼆分/滑动窗⼝) 题目解析 讲解算法原理 编写代码 不相邻取数(动态规划-线性dp) 题目解析 1.题目链接:不相…...

go 自己写序列化函数不转义
以map[int32]string转化为[]byte为例 背景:算法传给我一个map[int32]string类型的值(map的值本身是json转化成的string),我需要把这个值生成一个文件上传到OSS,但是发现通过url下载下来的文件里面有转义字符。 原因&a…...

一般行业安全管理人员考试题库分享
1.在高速运转的机械飞轮外部安装防护罩,属于(B)安全技术措施。 A.限制能量 B.隔离 C.故障设计 D.设置薄弱环节 2.生产经营单位的(B)是本单位安全生产的第一责任人,对落实本单位安全生产主体责任全面负责,具体履行安全生产管理职责。 A.全员 B…...

Marketo REST API 批量修改邮件内容
以下是更加细化的 使用 Marketo REST API 批量修改邮件内容 的步骤,详细解释每个阶段的操作,包括 API 的请求、数据处理及潜在问题解决。 前期准备工作 确保 Marketo API 访问权限 你需要 Marketo REST API 用户 和 API Role,有权限访问邮件资…...

《云原生安全攻防》-- K8s安全框架:认证、鉴权与准入控制
从本节课程开始,我们将来介绍K8s安全框架,这是保障K8s集群安全比较关键的安全机制。接下来,让我们一起来探索K8s安全框架的运行机制。 在这个课程中,我们将学习以下内容: K8s安全框架:由认证、鉴权和准入控…...

淘宝获取sku详细信息 API
淘宝获取 SKU 详细信息的 API 主要是 taobao.item_sku 接口,以下是详细介绍: 公共参数 key:调用 key,是调用接口的身份验证信息,必须以 GET 方式拼接在 URL 中1.secret:调用密钥,与 key 配合使…...

基于Spring Boot的体育商品推荐系统
一、系统背景与目的 随着电子商务的快速发展和人们健康意识的提高,体育商品市场呈现出蓬勃发展的态势。然而,传统的体育商品销售方式存在商品种类繁多、用户选择困难、个性化需求无法满足等问题。为了解决这些问题,基于Spring Boot的体育商品…...

C++小细节笔记
1、C字符串转数字 – 数字转字符串 //string > int 使用 stoi stol//int > string 使用 to_string()2、C遍历 int evalRPN(vector<string>& tokens) {stack<int> intStack;for(string &str:tokens){}bool isValid(string s) {stack<char> …...
)
go语言并发读写数据队列,不停写的同时,一次最多读取指定量数据(逐行注释)
1、数据队列可以存储任意类型的一个数据(下程序是添加整数值)。 数据队列代码点这里查看《go语言结构体实现数据结构队列(先进先出)存储数据(逐行注释)》 2、读写操作并发进行(下程序向队列中…...
密码学——密码学概述、分类、加密技术(山东省大数据职称考试)
大数据分析应用-初级 第一部分 基础知识 一、大数据法律法规、政策文件、相关标准 二、计算机基础知识 三、信息化基础知识 四、密码学 五、大数据安全 六、数据库系统 七、数据仓库. 第二部分 专业知识 一、大数据技术与应用 二、大数据分析模型 三、数据科学 密码学 大数据…...
【数据库MySQL篇二】MySQL数据库入门基础教程:一网打尽数据库和表各种操作、命令和语法
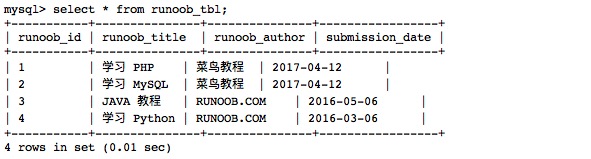
一、MySQL创建数据库 使用Create命令创建数据库 我们可以在登陆 MySQL 服务后,使用 create 命令创建数据库,语法如下: CREATE DATABASE 数据库名; 以下命令简单的演示了创建数据库的过程,数据名为 RUNOOB: [roothost]# mysql -u root -p…...

Android 解决“Could not resolve all artifacts for configuration ‘:classpath‘方法
前些天发现了一个蛮有意思的人工智能学习网站,8个字形容一下"通俗易懂,风趣幽默",感觉非常有意思,忍不住分享一下给大家。 👉点击跳转到教程 报错背景,公司的项目,长时间没有打开,时隔半年再次打…...

青少年编程与数学 02-004 Go语言Web编程 08课题、使用Gin框架
青少年编程与数学 02-004 Go语言Web编程 08课题、使用Gin框架 一、Gin框架二、接收和处理请求三、应用示例 课题摘要:本文介绍了Gin框架的特点、如何接收和处理请求以及一个应用示例。Gin是一个高性能、轻量级的Go语言Web框架,以其快速、极简设计、强大的路由和中间…...

PostgreSQL: 事务年龄
排查 在 PostgreSQL 数据库中,事务年龄(也称为事务 ID 年龄)是一个重要的监控指标,因为 PostgreSQL 使用事务 ID(XID)来保持事务的隔离性。每个事务都会被分配一个唯一的事务 ID,这个 ID 随着每…...

C# 识别二维码
文章目录 一. 二维码识别技术概述二 维码识别的步骤图像预处理二维码的定位和检测二维码解码 三 常用的二维码识别库1. OpenCV2. ZXing.Net 一. 二维码识别技术概述 二维码是一种通过黑白矩阵排列来编码数据的图形符号,它的编码方式具有较强的容错性,可以…...

KeepAlive与RouterView缓存
参考 vue动态组件<Component>与<KeepAlive> KeepAlive官网介绍 缓存之keep-alive的理解和应用 Vue3Vite KeepAlive页面缓存问题 vue多级菜单(路由)导致缓存(keep-alive)失效 vue3 router-view keeperalive对于同一路径但路径…...

RK3588 , mpp硬编码rgb, 保存MP4视频文件.
RK3588 , mpp硬编码yuv, 保存MP4视频文件. ⚡️ 传送 ➡️ RK3588, FFmpeg 拉流 RTSP, mpp 硬解码转RGBRk3588 FFmpeg 拉流 RTSP, 硬解码转RGBUbuntu x64 架构, 交叉编译aarch64 FFmpeg mppCode Init MppMPP_RET init_mpp...

使用 Wireshark 和 Lua 脚本解析通讯报文
在复杂的网络环境中,Wireshark 凭借其强大的捕获和显示功能,成为协议分析不可或缺的工具。然而,面对众多未被内置支持的协议或需要扩展解析的场景,Lua 脚本的引入为Wireshark 提供了极大的灵活性和可扩展性。本文将详细介绍如何使…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

