子页面访问父页面
子页面访问父页面的方式主要依赖于页面之间的关系,特别是它们是否处于同一域、是否是嵌套在 <iframe> 中、或者通过弹出窗口打开。下面是几种常见的子页面访问父页面的方法:
1. 通过 window.parent 访问父页面(适用于嵌套的 iframe)
当子页面是嵌套在父页面的 <iframe> 中时,子页面可以通过 window.parent 访问父页面的 DOM 和 JavaScript。这种方式适用于父子页面在同一域下的情况。
示例:
父页面:
<iframe src="child.html" id="myIframe"></iframe>
子页面(child.html):
// 子页面访问父页面的 DOM 元素
window.parent.document.getElementById('parent-element').innerText = "更新父页面内容";// 或者调用父页面的函数
window.parent.someFunction();
注意:
window.parent只能访问父页面的内容。如果子页面和父页面在不同域(跨域),则无法直接访问父页面的 DOM 和 JavaScript,需使用postMessage等方法进行通信。
相关文章:

子页面访问父页面
子页面访问父页面的方式主要依赖于页面之间的关系,特别是它们是否处于同一域、是否是嵌套在 <iframe> 中、或者通过弹出窗口打开。下面是几种常见的子页面访问父页面的方法: 1. 通过 window.parent 访问父页面(适用于嵌套的 iframe&am…...

芯片级IO (Pad) Ring IP Checklist
SoC top顶层数字后端实现都会涉及到IO Ring (PAD Ring)的设计。这里面包括VDD IO,VDDIO IO, Signal IO, Corner IO,Filler IO,IO power cut cell等等。 数字后端零基础入门系列 | Innovus零基础LAB学习Day2 数字IC后端实现TOP F…...

计算机毕业设计论文指导
计算机毕业设计论文指导 计算机毕业设计辅导一站式!太香了💪 [赞R][赞R][赞R]嗨喽!计算机专业的宝子们! 计算机毕设辅导专业靠谱的他来了!! 是不是还在为选题程序不会做而感到苦难? 论文没思路赶…...

Electron-Vue 开发下 dev/prod/webpack server各种路径设置汇总
背景 在实际开发中,我发现团队对于这几个路径的设置上是纯靠猜的,通过一点点地尝试来找到可行的路径,这是不应该的,我们应该很清晰地了解这几个概念,以下通过截图和代码进行细节讲解。 npm run dev 下的路径如何处理&…...

Vue.js前端框架教程9:Vue插槽slot用法
文章目录 插槽(Slots)无名插槽(默认插槽)具名插槽reference 插槽使用 v-slot 的缩写语法 插槽(Slots) 在 Vue 中,插槽(Slots)是一种组件内容分发的机制,允许…...

初学stm32 --- NVIC中断
目录 STM32 NVIC 中断优先级管理 NVIC_Type: ISER[8]: ICER[8]: ISPR[8]: ICPR[8]: IABR[8]: IP[240]: STM32 的中断分组: 中断优先级分组函数 NVIC_PriorityGroupConfig 中断初始化函…...

Jest 入门指南:从零开始编写 JavaScript 单元测试
前言 在前端开发中,单元测试已经成为确保代码质量和稳定性的关键步骤。Jest 作为由 Facebook 开发和维护的功能强大的 JavaScript 测试框架,以其易于配置、丰富的功能和开箱即用的特性,成为众多开发者的首选工具。本文旨在引导你从零开始&am…...

【Java Web】Axios实现前后端数据异步交互
目录 一、Promise概述 二、Promise基本用法 三、async和await关键字 四、Axios介绍 4.1 Axios基本用法 4.2 Axios简化用法之get和post方法 五、Axios拦截器 六、跨域问题处理 一、Promise概述 axios是代替原生的ajax实现前后端数据交互的一套新解决方案,而…...

React 第十七节 useMemo用法详解
概述 useMemo 是React 中的一个HOOK,用于根据依赖在每次渲染时候缓存计算结果; 大白话就是,只有依赖项发生变化时候,才会重新渲染为新计算的值,否则就还是取原来的值,有点类似 vue 中的 computed 计算属性…...

鸿蒙项目云捐助第十五讲云数据库的初步使用
鸿蒙项目云捐助第十五讲云数据库的初步使用 在华为云技术使用中,前面使用了云函数,接下来看一下华为云技术中的另外一个技术云数据库的使用。 一、云数据库的创建 这里使用华为云数据库也需要登录到AppGallery Connect平台中,点击进入到之…...

如何构建一个可信的联邦RAG系统。
今天给大家分享一篇论文。 题目是:C-RAG:如何构建一个可信的联邦检索RAG系统。 论文链接:https://arxiv.org/abs/2412.13163 论文概述 尽管大型语言模型 (LLM) 在各种应用中展现出令人印象深刻的能力,但它们仍然存在可信度问题ÿ…...

【深度学习之三】FPN与PAN网络详解
FPN与PAN:深度学习中的特征金字塔网络与路径聚合网络 在深度学习的领域里,特征金字塔网络(Feature Pyramid Networks,简称FPN) 和 路径聚合网络(Path Aggregation Network,简称PAN)…...

Qt学习笔记第71到80讲
第71讲 事件过滤器的方式实现滚轮按键放大 事件体系(事件派发 -> 事件过滤->事件分发->事件处理)中,程序员主要操作的是事件分发与事件处理。我们之前已经通过继承QTextEdit来重写事件实现Ctrl加滚轮的检测,还有一种处理…...

以管理员身份运行
同时按下Ctrl Shift Esc键打开任务管理器,在任务管理器的左上角,点击“文件”菜单,在下拉菜单中选择“新建任务” 在弹出的对话框中,输入您想要运行的程序的名称。如果您不确定程序的确切名称,可以点击“浏览”来找到…...

用 Python 实现井字棋游戏
一、引言 井字棋(Tic-Tac-Toe)是一款经典的两人棋类游戏。在这个游戏中,玩家轮流在 3x3 的棋盘上放置自己的标记,通常是 “X” 和 “O”,第一个在棋盘上连成一线(横、竖或斜)的玩家即为获胜者。…...
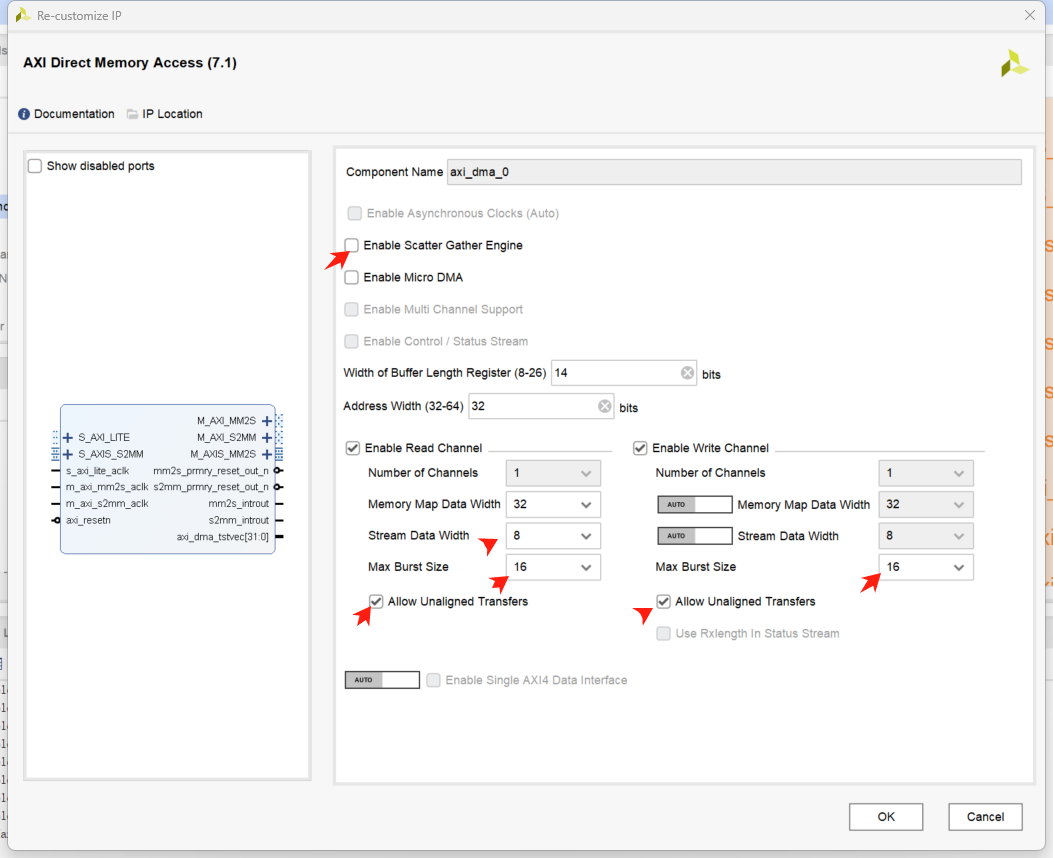
06 实现自定义AXI DMA驱动
为什么要实现自定义AXI DMA驱动 ZYNQ 的 AXI DMA 在 Direct Register DMA (即 Simple DMA)模式下可以通过 AXIS 总线的 tlast 提前结束传输,同时还可以在 BUFFLEN 寄存器中读取到实际传输的字节数,但是通过 Linux 的 DMA 驱动框架…...

SpringBoot集成ENC对配置文件进行加密
在线MD5生成工具 配置文件加密,集成ENC 引入POM依赖 <!-- ENC配置文件加密 --><dependency><groupId>com.github.ulisesbocchio</groupId><artifactId>jasypt-spring-boot-starter</artifactId><version>2.1.2</ver…...

初学stm32 ——— 串口通信
目录 STM32的串口通信接口 UART异步通信方式特点: 串口通信过程 STM32串口异步通信需要定义的参数: USART框图: 常用的串口相关寄存器 串口操作相关库函数 编辑 串口配置的一般步骤 STM32的串口通信接口 UART:通用异步收发器USART&am…...

qwt 多Y轴 项目效果
项目场景: 在做一个半导体上位机软件项目实践中,需要做一个曲线展示和分析界面,上位机主题是用qt框架来开发,考虑到目前qt框架的两种图标库,一个是qcustomplot 一个是 qwt。之所以采用qwt ,根本原因是因为…...

Java中通过ArrayList扩展数组
在Java中,ArrayList 是一个动态数组实现,能够根据需要自动调整其大小。与传统的数组不同,ArrayList 不需要预先指定大小,并且提供了许多方便的方法来操作集合中的元素。下面将详细介绍如何使用 ArrayList 进行数组的扩展ÿ…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
