思科CCNA认证都学什么考什么?
关注 工 仲 好:IT运维大本营
CCNA考试要学的东西很多,你不要看它只是一个初级认证,但是它的专业内容知识是不少的,你想要学好也是需要下一番苦功的。
那么考CCNA需要学哪些东西呢?下面我们就来了解一下吧。
01、考CCNA需要学哪些东西
1、网络基础原理篇,这部分包含了很多琐碎的知识点,刚开始的时候会感觉很枯燥,没办法,做技术就要有心理准备。
2、二层交换技术篇,这一部分主要介绍了交换的原理和组网方式。
3、三层路由技术篇,主要讲解常见的路由协议原理和配置。
4、网络运用篇,包括DHCP、NAT、ACL等。
所以CCNA的体系很明显:基础原理----局域网----广域网----实战运用。
02、CCNA怎么考证
1、报考条件
要考CCNA,首先要看看自己是否具备报考资格。
CCNA作为初级思科认证,报名其实没什么条件限制,凡具有DOS、Windows和一定英语水平的在职人员、各大专院校在校学生及要求获得网络关键设备技术知识的人员都是可以报名参加思科认证考试。
不过年龄上需要满18周岁,16周岁到18周岁之间,需要监护人的同意。
2、报名方式
CCNA的报名方式主要有三种。
第一种是使用Pearsen VUE的在线服务,通过网站注册考试;
第二种是通过培训机构报名考试;
第三种则是打客服电话。
3、考试形式及内容
思科认证考试内容主要为Cisco网络设备互连(ICND)。
在新版认证体系中,CCNA不细分认证方向,CCNA原先所有方向(除Cyber Ops外)合并,统一只考一门。
考试代码:200-301
考试时间:120分钟
考场题量:102题
考试分数:满分1000分,825分通过
考试题型:单选、多选、拖图题
★ CCNA的主要考试内容包括:
1、 广域网络设计思路及原则。
2、 OSI七层模型,智能型以太网交换机或路由器的常用操作 。
3、 使用Cisco软件在WAN环境中,配置各种路由器、交换机 设备的IP地址。
4、 Cisco路由器和交换机的密码恢复、IOS更新。
5、 根据给定的网络设计规范,连接Cisco交换机和路由器 。
6、 配置路由器所支持的路由协议,如RIP、IGRP、EIGRP、 OSPF等 。
7、 配置交换机,在上千台主机间实现VLAN的设置和互连 。
8、 配置访问列表,以实现安全控制,过滤网络流量以及对 某些设备或网段的访问。
9、 配置WAN线路(专线、ISDN备份和帧中继)。
10、验证Cisco路由器和交换机配置的网络协议。
11、通过Cisco IOS命令和常用网管软件分析、解决网络故障。
12、NAT(网络地址翻译)。
13、VLSM(可变长度的子网掩码)
相关文章:

思科CCNA认证都学什么考什么?
关注 工 仲 好:IT运维大本营CCNA考试要学的东西很多,你不要看它只是一个初级认证,但是它的专业内容知识是不少的,你想要学好也是需要下一番苦功的。 那么考CCNA需要学哪些东西呢?下面我们就来了解一下吧。 01、考CCN…...
模型部署学习笔记——模型部署关键知识点总结
模型部署学习笔记——模型部署关键知识点总结 模型部署学习笔记——模型部署关键知识点总结1. CUDA中Grid和Block的定义是什么?Shared Memory的定义?Bank Conflict的定义?Stream和Event的定义?2. TensorRT的工作流程?3…...

22智能 狄克斯特拉算法复习
狄克斯特拉算法 图 根据边有无方向分为: 有向图、无向图 根据边有无权重变量分为: 有权图、无权图 根据顶点是否连通分为: 连通图和非连通图入度:表示有多少条边指向该顶点出度:表示有多少条边从该顶点指出算法步骤&a…...

首个!艾灵参编的工业边缘计算国家标准正式发布
近日,艾灵参与编制的《面向工业应用的边缘计算 应用指南》(以下简称《标准》)国家标准正式发布,将于2025年5月1日起实施。这一里程碑式的成果,不仅标志着我国在工业边缘计算技术标准化领域取得了重大突破,成…...

curl也支持断点续传
curl断点续传 访问外网资源,特别是Github上比较大的资源,例如,笔者遇到的calico发布包,经常会遇到在浏览器上下载半途中断。 那么支持断点续传的下载工具,就是应对这种情况的好帮手! 简单的断点续传工具…...
交换机链路聚合(手动负载分担模式)(eNSP)
目录 交换机SW_C配置: 交换机-PC划分vlan: 交换机-交换机端口聚合: 交换机SW_D配置: 交换机-PC划分vlan: 交换机-交换机端口聚合: 验证: 链路聚合的端口清除: 交换机端口聚合的存在意义主要有以下几点: 增加带宽 提高冗余性和可靠性 实现负载均衡 降低成本 …...
jmeter 接口性能测试 学习笔记
目录 说明工具准备工具配置jmeter 界面汉化配置汉化步骤汉化结果图 案例1:测试接口接口准备线程组添加线程组配置线程组值线程数(Number of Threads)Ramp-Up 时间(Ramp-Up Period)循环次数(Loop Count&…...

`HashMap`、`Hashtable` 和 `HashSet`的区别
HashMap、Hashtable 和 HashSet 都是 Java 中常用的集合类,它们的功能和实现有所不同,尽管它们都使用哈希表(hash table)作为底层数据结构。以下是它们之间的主要区别: 1. HashMap 和 Hashtable 的区别 特性HashMapH…...
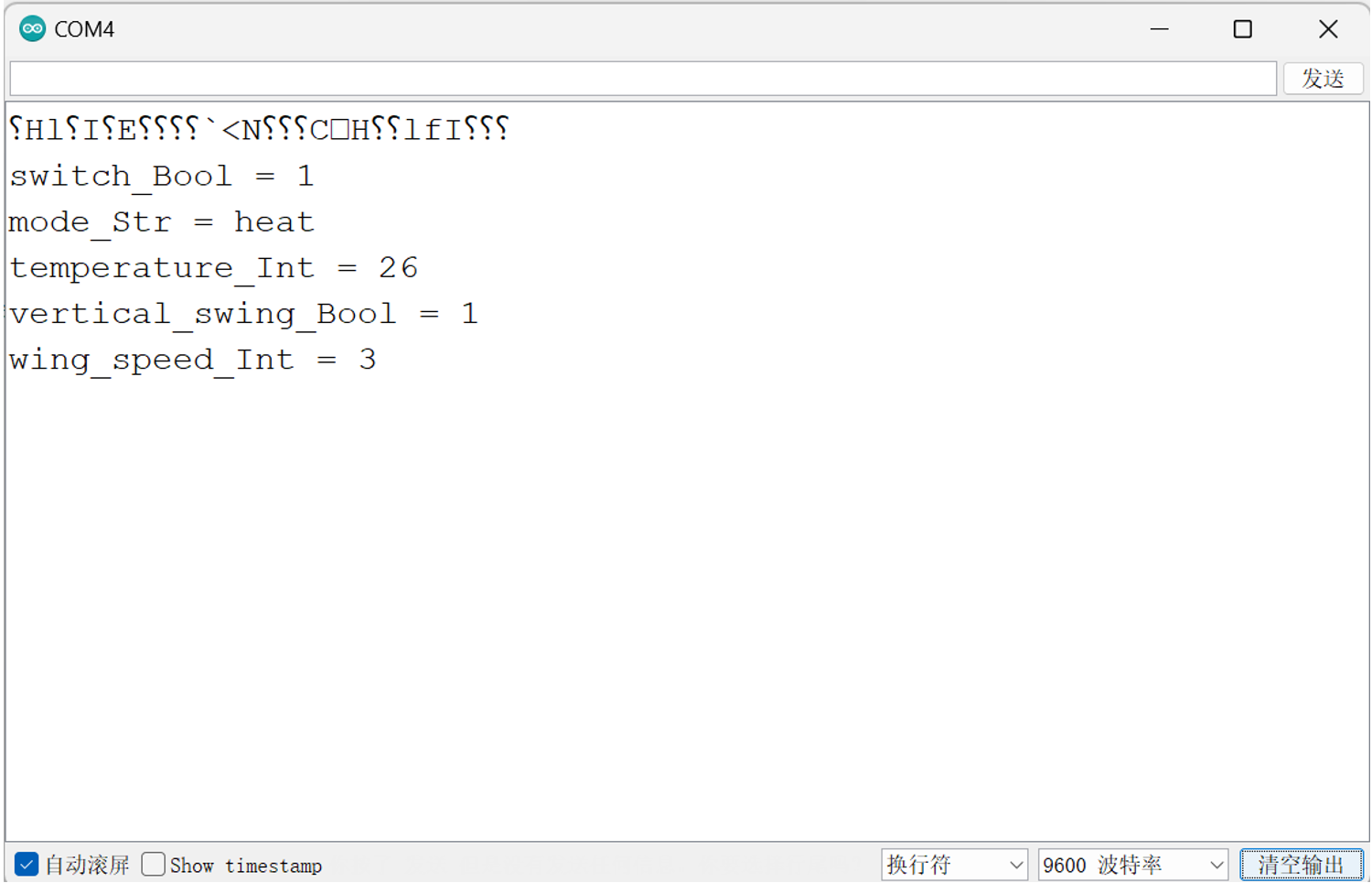
Arduino中解析JSON数据
JSON JSON(JavaScript Object Notation,即JavaScript对象表示法)是一种广泛采用的开放标准文件格式与数据交换格式。它兼具人类可读性和机器易解析性,使得数据的编写、阅读、生成及解析都变得十分便捷。JSON的设计不依赖于特定编…...

linux----文件访问(c语言)
linux文件访问相关函数 打开文件函数 - open 函数原型:int open(const char *pathname, int flags, mode_t mode);参数说明: pathname:这是要打开的文件的路径名,可以是绝对路径或者相对路径。例如,"/home/user/…...

源码分析之Openlayers中MousePosition鼠标位置控件
概述 本文主要介绍 Openlayers 中的MousePosition鼠标位置控件,该控件会创建一个元素在页面的右上方用来实时显示鼠标光标的位置坐标。该控件在实际应用很有效,可以实时获取鼠标位置,但是一般控件元素都会自定义。 源码分析 MousePosition…...

以ATTCK为例构建网络安全知识图
ATT&CK(Adversarial Tactics, Techniques, and Common Knowledge )是一个攻击行为知识库和模型,主要应用于评估攻防能力覆盖、APT情报分析、威胁狩猎及攻击模拟等领域。本文简单介绍ATT&CK相关的背景概念,并探讨通过ATT&a…...

myexcel的使用
参考: (1)api文档:https://www.bookstack.cn/read/MyExcel-2.x/624d8ce73162300b.md (2)源代码: https://github.com/liaochong/myexcel/issues 我: (1)m…...

Unity 上好用的插件
PlayerMaker BehaviorDesigner Cinemachine Timeline Hybrid Addressable AssetBundle Blower Simple Zoom 大地图上缩放和平移使用ScrollRect的好效果实现...

Vivado - 远程调试 + 远程综合实现 + vmWare网络配置 + NFS 文件共享 + 使用 VIO 核
目录 1. 简介 2. VIO 配置 2.1 VIO IP 2.2 VIO 对比 ILA 3. VIO 示例 3.1 Led 3.1.1 工程配置 3.1.2 效果展示 3.2 Key 3.2.1 工程配置 3.2.1 效果展示 3.3 门控触发 3.3.1 工程配置 3.3.2 效果展示 4. 远程调试 4.1 配置目标主机 4.2 配置本机 4.3 vmWare 网…...

双臂机器人
目录 一、双臂机器人简介 二、双臂机器人系统的组成 三、双臂机器人面临的主要挑战 3.1 协调与协同控制问题 3.2 力控制与柔顺性问题 3.3 路径规划与轨迹优化问题 3.4 感知与环境交互 3.5 人机协作问题 3.6 能源与效率问题 3.7 稳定性与可靠性问题 四、双臂机器人…...

【Lua热更新】上篇
Lua 热更新 - 上篇 下篇链接:【Lua热更新】下篇 文章目录 Lua 热更新 - 上篇一、AssetBundle1.理论2. AB包资源加载 二、Lua 语法1. 简单数据类型2.字符串操作3.运算符4.条件分支语句5.循环语句6.函数7. table数组8.迭代器遍历9.复杂数据类型 - 表9.1字典9.2类9.3…...

Ubuntu批量修改文件名
文章目录 批量重命名文件:Ubuntu下使用find命令结合sed和mv参考 批量重命名文件:Ubuntu下使用find命令结合sed和mv 在日常开发和文件管理中,有时我们需要批量重命名一批文件,比如将文件名中的某个特定字符串替换为另一个字符串。…...

食家巷大烤馍:岁月沉淀下的麦香传奇
在繁华都市的街角巷尾,隐藏着许多不为人知的美食宝藏,食家巷大烤馍便是其中之一。它宛如一位低调的美食大师,默默散发着独特的魅力,用最质朴的味道,征服着每一个过往食客的味蕾。 初见食家巷大烤馍,你会被…...

harmony UI组件学习(1)
Image 图片组件 string格式,通常用来加载网络图片,需要申请网络访问权限:ohos.permission.INTERNET Image(https://xxx.png) PixelMap格式,可以加载像素图,常用在图片编辑中 Image(pixelMapobject) Resource格式,加…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
