C语言版解法力扣题:将整数按权重排序
1.题目描述
我们将整数 x 的 权重 定义为按照下述规则将 x 变成 1 所需要的步数:
如果 x 是偶数,那么 x = x / 2
如果 x 是奇数,那么 x = 3 * x + 1
比方说,x=3 的权重为 7 。因为 3 需要 7 步变成 1 (3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1)。
给你三个整数 lo, hi 和 k 。你的任务是将区间 [lo, hi] 之间的整数按照它们的权重 升序排序 ,如果大于等于 2 个整数有 相同 的权重,那么按照数字自身的数值 升序排序 。
请你返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。
注意,题目保证对于任意整数 x (lo <= x <= hi) ,它变成 1 所需要的步数是一个 32 位有符号整数。
2.案例演示:
示例 1:
输入:lo = 12, hi = 15, k = 2
输出:13
解释:12 的权重为 9(12 --> 6 --> 3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1)
13 的权重为 9
14 的权重为 17
15 的权重为 17
区间内的数按权重排序以后的结果为 [12,13,14,15] 。对于 k = 2 ,答案是第二个整数也就是 13 。
注意,12 和 13 有相同的权重,所以我们按照它们本身升序排序。14 和 15 同理。
示例 2:
输入:lo = 7, hi = 11, k = 4
输出:7
解释:区间内整数 [7, 8, 9, 10, 11] 对应的权重为 [16, 3, 19, 6, 14] 。
按权重排序后得到的结果为 [8, 10, 11, 7, 9] 。
排序后数组中第 4 个数字为 7 。
提示:
1 <= lo <= hi <= 1000
1 <= k <= hi - lo + 1
3.思路描述:
1.定义权重:
·权重是指将整数 x变为 1 所需的步骤数。根据题目规则:·如果 x是偶数,则 x=x/2。
·如果 x是奇数,则 x=3*x+1。
我们需要编写一个函数来计算每个整数的权重。
2.遍历区间:
遍历给定的区间[1o,hi],计算每个整数的权重,并将其存储在一个数组中。
3. 排序:
对存储权重和对应数字的数组进行排序。排序的规则是:首先按权重升序排列。
如果权重相同,则按数字本身升序排列。.
4.返回结果
排序完成后,返回排序后的数组中第k个数字。
4.具体步骤:
1.计算权重的函数 :
创建一个函数 weight(int x),使用循环来计算 x变为 1 所需的步骤数。
2.存储区间内的数字:
在 getKth(int 1o,int hi,int k)函数中,创建一个数组来存储区间[1o,hi]内的所有整数。
3. 排序:
使用C标准库中的 qsort 函数,定义一个比较函数来根据权重和数字进行排序。
4.获取第k 个数字:
排序完成后,直接返回数组中第 k-1个元素(因为数组索引从 0开始)
5.代码:
//计算权重函数
int weight(int x) {int steps = 0;while (x != 1) {if (x % 2 == 0) {x /= 2;} else {x = 3 * x + 1;}steps++;}return steps;
}// 比较函数,用于排序
int compare(const void *a, const void *b) {int weightA = weight(*(int*)a);int weightB = weight(*(int*)b);if (weightA == weightB) {return (*(int*)a - *(int*)b); // 如果权重相同,按数字升序}return weightA - weightB; // 按权重升序
}// 主函数:获取区间 [lo, hi] 内第 k 个数字按权重排序后的结果
int getKth(int lo, int hi, int k) {int n = hi - lo + 1; // 计算区间内数字的个数int numbers[n]; // 存储区间内的所有数字// 将区间内的数字存入数组for (int i = 0; i < n; i++) {numbers[i] = lo + i;}// 使用 qsort 函数进行排序qsort(numbers, n, sizeof(int), compare);// 返回排序后的第 k 个数字return numbers[k - 1];
}6.补充说明(源于菜鸟教程):

相关文章:

C语言版解法力扣题:将整数按权重排序
1.题目描述 我们将整数 x 的 权重 定义为按照下述规则将 x 变成 1 所需要的步数: 如果 x 是偶数,那么 x x / 2 如果 x 是奇数,那么 x 3 * x 1 比方说,x3 的权重为 7 。因为 3 需要 7 步变成 1 (3 --> 10 -->…...

Unity ECS和OOP优劣对比
OOP的优劣 面向对象编程(OOP, Object-Oriented Programming)是一种通过对象及其交互来组织代码的编程范式,广泛应用于软件开发中。以下是OOP的优缺点: 优点 代码可重用性 继承机制:通过继承,子类可以复用…...

【Java基础面试题026】Java中的String、StringBuffer和StringBuilder的区别是什么?
回答重点 他们都是Java中处理字符串的类,区别主要体现在可变性、线程安全和性能上 1)String 不可变:String是不可变类,字符串对象创建,存储在堆中,字符串内容存储在字符串常量池中,一旦创建内…...
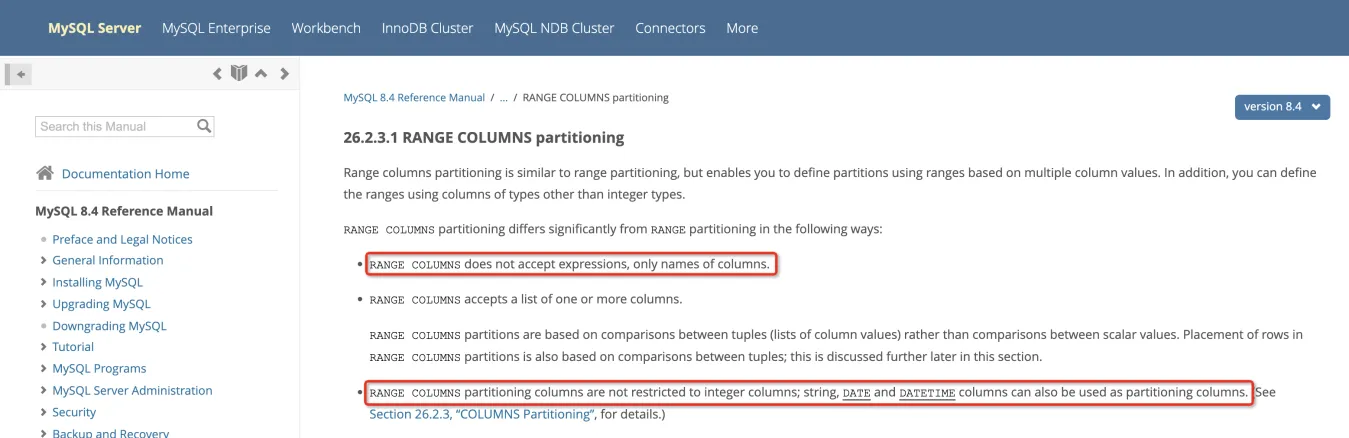
解析在OceanBase创建分区的常见问题|OceanBase 用户问题精粹
在《分区策略和管理分区计划的实践方案》这篇文章中,我们介绍了在ODC中制定分区策略及有效管理分区计划的经验。有不少用户在该帖下提出了使用中的问题,其中一个关于创建分区的限制条件的问题,也是很多用户遭遇的老问题。因此本文以其为切入&…...

Flutter组件————Container
Container Container 是 Flutter 中最常用的布局组件之一 参数 参数名称类型描述alignmentAlignmentGeometry定义子组件在其内部的对齐方式,默认为 null,即不改变子组件的位置。paddingEdgeInsetsGeometry内边距,用于在子组件周围添加空间…...
:SpringMyBatis)
Java重要面试名词整理(二):SpringMyBatis
文章目录 Spring篇Spring核心推断构造方法AOP动态代理Advice的分类Advisor的理解AOP相关的概念 定义BeanASM技术JFR依赖注入循环依赖LifecycleSpring AOT Spring事务Spring事务传播机制Spring事务传播机制是如何实现的呢?Spring事务传播机制分类 SpringMVCHandlerHandlerMappi…...

Excel生成DBC脚本源文件
Excel制作 新建一个Excel,后缀为“.xls” 工作本名称改为“CAN_Matrix” 在首行按照列来起名字,在里面只需要填写必须的内容即可。 列数名称第0列Message Name第1列Message Format第2列Message ID第3列Message Length (byte)第4列Message Transmitte…...

Git进阶:本地或远程仓库如何回滚到之前的某个commit
在Git的使用过程中,我们经常会遇到需要回滚到之前某个commit的情况。无论是为了修复错误、撤销更改,还是为了重新组织代码,回滚到特定commit都是一个非常有用的技能。本文将介绍几种常用的回滚方法,帮助读者更好地掌握Git版本控制…...
)
linux 中文输入法设置的宏观思路 (****)
乱是永远的不乱,变是永远的不变。 $ ibus help # 注意:help 前没有杠符号 $ setxkbmap -help # 注意:help 前只有一个杠符号 $ localectl --help # 注意:help 前有 2 个杠符号 $ man im-config # 注意:-h, --help 只出来提示信息:请参考。。。。。。。 $ man abc…...

271-基于XC7V690T的12路光纤PCIe接口卡
一、板卡概述 基于XC7V690T的12路光纤PCI-E接口卡,用于实现多通道高速光纤数据接收和发送,板卡兼容PCIe 2.0和PCIe 3.0规范,利用PCI-E Switch PEX 8748实现FPGA芯片与计算机的通信,计算机与板卡接口处提供PCI-e 16速接口ÿ…...

Semaphore UI安装和实践
本次实验环境采用centos7.9操作系统,使用rpm包安装方式。 1.配置yum源 --下载centos华为云镜像仓库 wget -O /etc/yum.repos.d/CentOS-Base.repo https://mirrors.huaweicloud.com/repository/conf/CentOS-7-anon.repo[rootlocalhost ~]# wget -O /etc/yum.repos.…...

Redis篇--常见问题篇7--缓存一致性2(分布式事务框架Seata)
1、概述 在传统的单体应用中,事务管理相对简单,通常使用数据库的本地事务(如MySQL的BEGIN和COMMIT)来保证数据的一致性。然而,在微服务架构中,由于每个服务都有自己的数据库,跨服务的事务管理变…...

Docker Compose 安装 Harbor
我使用的系统是rocky Linux 9 1. 准备环境 确保你的系统已经安装了以下工具: DockerDocker ComposeOpenSSL(用于生成证书)#如果不需要通过https连接的可以不设置 1.1 安装 Docker 如果尚未安装 Docker,可以参考以下命令安装&…...

使用docker compose安装gitlab
使用docker compose安装gitlab GitLab简介设置GITLAB_HOME路径创建docker挂载目录获取可用的GitLab版本编写docker-compose.yml文件启动docker基础配置GITLAB_OMNIBUS_CONFIG修改配置 中文设置数据库配置系统邮箱配置 GitLab简介 GitLab是一个基于Git的开源项目,…...

大模型日报 2024-12-18
大模型日报 2024-12-18 大模型资讯 标题: 3B模型长思考后击败70B!HuggingFace逆向出o1背后技术细节并开源 摘要:这篇文章探讨了小模型在经过长时间思考后,如何在性能上超越更大规模模型的现象。HuggingFace通过逆向工程和开源技术…...

Linux安装mysql5.7
一、下载mysql5.7 首先我们需要去下载linux版本的mysql-5.7.24的安装包。 1.可以去官方网站链接: https://downloads.mysql.com/archives/community/ ,下载mysql-5.7.24-linux-glibc2.12-x86_64.tar压缩包。 2.在线下载,使用wget命令,直接从官网下载…...

【容器】k8s学习笔记原理详解(十万字超详细)
Pod详解 Pod介绍 Pod结构 每个Pod中都可以包含一个或者多个容器,这些容器可以分为两类: 用户程序所在的容器,数量可多可少Pause容器,这是每个Pod都会有的一个根容器,它的作用有两个: 可以以它为依据&am…...

.NET重点
B/S C/S B/S: 浏览器端:JavaScript,HTML,CSS 服务器端:ASP(.NET)PHP/JSP 优势:维护方便,易于升级和扩展 劣势:服务器负担沉重 C/S java/.NET/VC系列 …...

SMMU软件指南SMMU编程之虚拟机结构和缓存
安全之安全(security)博客目录导读 目录 一、虚拟机结构(VMS) 二、缓存 一、虚拟机结构(VMS) 虚拟机结构(VMS)是SMMU中的概念,是一个由STE.VMSPtr字段指向的结构,包含每个虚拟机的配置设置。在相同安全状态下具有相同虚拟机ID(VMID)的多个STE必须指向相同的VMS。…...

Go 语言并发实战:利用协程处理多个接口进行数据融合
高效地处理多个数据源并将其整合为有意义的结果是开发中一项重要的任务。Go 语言,以其强大的并发特性,为我们提供了优雅而高效的解决方案。那么我们探讨一下如何利用 Go 语言的协程,同时调用多个接口获取数据,并将这些数据无缝地合…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
