语音增强的损失函数选择
一、最优尺度不变信噪比(OSISNR)损失函数
参考:论文解读 --Optimal scale-invariant signal-to-noise ratio and curriculum learning for monaural multi-spea
最优尺度不变信噪比(OSI-SNR)是一种用于评估信号质量的指标,特别是在语音分离和增强任务中。OSI-SNR 通过优化估计信号与目标信号之间的相似性,提供了一种更稳定和可靠的信号质量度量。OSI-SNR 的计算步骤如下: s s s表示原始语音信号, s ^ \hat{s} s^表示重建的语音信号。
⟨ s , s ^ ⟩ = ∑ t = 1 T s [ t ] ⋅ s ^ [ t ] \langle s, \hat{s} \rangle = \sum_{t=1}^{T} s[t] \cdot \hat{s}[t] ⟨s,s^⟩=t=1∑Ts[t]⋅s^[t]
∣ s ^ ∣ 2 = ∑ t = 1 T ∣ s ^ [ t ] ∣ 2 |s^{\hat{}}|^2 = \sum_{t=1}^{T} |\hat{s}[t]|^2 ∣s^∣2=t=1∑T∣s^[t]∣2
λ = ∣ s ^ ∣ 2 ⟨ s , s ^ ⟩ \lambda = \frac{|s^{\hat{}}|^2}{\langle s, \hat{s} \rangle} λ=⟨s,s^⟩∣s^∣2
s target = λ ⋅ s ^ s_{\text{target}} = \lambda \cdot \hat{s} starget=λ⋅s^
e noise = s ^ − s target e_{\text{noise}} = \hat{s} - s_{\text{target}} enoise=s^−starget
OSI-SNR = 10 log 10 ( ∥ s target ∥ 2 ∥ e noise ∥ 2 ) \text{OSI-SNR} = 10 \log_{10} \left( \frac{\| s_{\text{target}} \|^2}{\| e_{\text{noise}} \|^2} \right) OSI-SNR=10log10(∥enoise∥2∥starget∥2)
将 最优尺度不变信噪比(OSI-SNR) 的倒数作为损失函数是一个合理的想法,尤其是在某些情况下,可能会更好地反映模型的性能。OSI-SNR 是一个衡量信号质量的指标,值越高表示信号质量越好。在训练过程中,我们通常希望最小化损失函数,因此可以考虑将 OSI-SNR 的倒数作为损失函数。参考:基于深层声学特征的端到端语音分离
方法 1:每一帧的 OSI-SNR 取倒数计算损失,再取均值
- 计算每一帧的 OSI-SNR:
OSI-SNR i = 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) \text{OSI-SNR}_i = 10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) OSI-SNRi=10log10(∥enoise,i∥2∥starget,i∥2) - 计算损失:
Loss i = 1 OSI-SNR i + ϵ = 1 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) + ϵ \text{Loss}_i = \frac{1}{\text{OSI-SNR}_i + \epsilon} = \frac{1}{10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) + \epsilon} Lossi=OSI-SNRi+ϵ1=10log10(∥enoise,i∥2∥starget,i∥2)+ϵ1 - 取均值:
Final Loss = 1 N ∑ i = 1 N Loss i = 1 N ∑ i = 1 N 1 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) + ϵ \text{Final Loss} = \frac{1}{N} \sum_{i=1}^{N} \text{Loss}_i = \frac{1}{N} \sum_{i=1}^{N} \frac{1}{10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) + \epsilon} Final Loss=N1i=1∑NLossi=N1i=1∑N10log10(∥enoise,i∥2∥starget,i∥2)+ϵ1
方法 2:每一帧的 OSI-SNR 取均值,再取倒数计算损失
- 计算每一帧的 OSI-SNR:
OSI-SNR i = 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) \text{OSI-SNR}_i = 10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) OSI-SNRi=10log10(∥enoise,i∥2∥starget,i∥2) - 取均值:
Mean OSI-SNR = 1 N ∑ i = 1 N OSI-SNR i = 1 N ∑ i = 1 N 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) \text{Mean OSI-SNR} = \frac{1}{N} \sum_{i=1}^{N} \text{OSI-SNR}_i = \frac{1}{N} \sum_{i=1}^{N} 10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) Mean OSI-SNR=N1i=1∑NOSI-SNRi=N1i=1∑N10log10(∥enoise,i∥2∥starget,i∥2) - 计算损失:
Final Loss = 1 Mean OSI-SNR + ϵ = 1 1 N ∑ i = 1 N 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) + ϵ \text{Final Loss} = \frac{1}{\text{Mean OSI-SNR} + \epsilon} = \frac{1}{\frac{1}{N} \sum_{i=1}^{N} 10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) + \epsilon} Final Loss=Mean OSI-SNR+ϵ1=N1∑i=1N10log10(∥enoise,i∥2∥starget,i∥2)+ϵ1
- 方法 1 的最终损失函数是对每一帧的 OSI-SNR 值取倒数后再取均值,强调了每一帧的信号质量。
- 方法 2 的最终损失函数是先计算所有帧的 OSI-SNR 的均值,然后取倒数,提供了一个整体的信号质量评估。
import numpy as np
def calculate_osi_snr_frame(target, estimated):# 获取帧数和频点数num_bins, num_frames = target.shapeosi_snr_frames = np.zeros(num_frames)for frame in range(num_frames):dot_product = np.sum(target[:, frame] * estimated[:, frame])estimated_energy = np.sum(np.abs(estimated[:, frame]) ** 2)lambda_opt = estimated_energy / (dot_product + 1e-10) # 防止除以零target_adjusted = lambda_opt * target[:, frame]noise = estimated[:, frame] - target_adjustedtarget_energy = np.sum(np.abs(target_adjusted) ** 2)noise_energy = np.sum(np.abs(noise) ** 2)osi_snr_frames[frame] = 10 * np.log10(target_energy / (noise_energy + 1e-8))return osi_snr_frames
def loss_method_1(osi_snr_frames, epsilon=1e-8):# 每一帧的 OSI-SNR 取倒数计算损失,再取均值losses = 1 / (osi_snr_frames + epsilon)final_loss = np.mean(losses)return final_loss
def loss_method_2(osi_snr_frames, epsilon=1e-8):# 每一帧的 OSI-SNR 取均值,再取倒数计算损失mean_osi_snr = np.mean(osi_snr_frames)final_loss = 1 / (mean_osi_snr + epsilon)return final_loss
# 示例掩蔽矩阵 M1 和 M2
M1 = np.array([[0.5, 0.6, 0.7],[0.8, 0.9, 1.0],[1.1, 1.2, 1.3]])M2 = np.array([[0.4, 0.5, 0.6],[0.7, 0.8, 0.9],[1.0, 1.1, 1.2]])
# 计算每一帧的 OSI-SNR
osi_snr_frames = calculate_osi_snr_frame(M1, M2)
# 计算损失
loss1 = loss_method_1(osi_snr_frames)
loss2 = loss_method_2(osi_snr_frames)
print(f"Loss Method 1 (Frame-wise OSI-SNR): {loss1:.4f}")
print(f"Loss Method 2 (Mean OSI-SNR): {loss2:.4f}")
Loss Method 1 (Frame-wise OSI-SNR): 0.03342
Loss Method 2 (Mean OSI-SNR): 0.03333
二、幅度幂律压缩均方误差(MC-MSE)损失函数
在音频信号处理和深度学习领域,幅度幂律压缩均方误差(Magnitude Compression Mean Squared Error, MC-MSE)是一种重要的损失函数,特别适用于语音增强和音频分离任务。MC-MSE通过引入幅度压缩的概念,能够更有效地处理具有大动态范围的音频信号,从而提高模型的性能。
2.1 、原理
在传统的均方误差(MSE)损失函数中,模型对大幅度信号的敏感性可能导致对小幅度信号的学习不足。这种情况在音频信号处理中尤为明显,因为音频信号的幅度通常具有很大的动态范围。为了解决这个问题,MC-MSE引入了幅度压缩的机制,通过对信号幅度进行非线性变换,使得模型在训练过程中能够更好地关注小幅度信号的特征。
MC-MSE的核心思想是通过幂律压缩函数对信号幅度进行处理,从而使得损失函数在计算时能够更均衡地反映不同幅度信号的影响。具体来说,MC-MSE通过对目标信号和预测信号的幅度进行压缩,来计算它们之间的均方误差。
2.2、公式
MC-MSE Loss的计算公式可以表示为:
L MC-MSE = 1 N ∑ i = 1 N ( compress ( y i ) − compress ( y ^ i ) ) 2 L_{\text{MC-MSE}}= \frac{1}{N} \sum_{i=1}^{N} \left( \text{compress}(y_i) - \text{compress}(\hat{y}_i) \right)^2 LMC-MSE=N1i=1∑N(compress(yi)−compress(y^i))2
其中:
- y i y_i yi 是目标信号的幅度。
- y ^ i \hat{y}_i y^i 是模型预测的幅度。
- compress ( ⋅ ) \text{compress}(\cdot) compress(⋅) 是幅度压缩函数,通常采用幂律压缩形式。
幅度压缩函数的形式为:
compress ( x ) = sign ( x ) ⋅ ∣ x ∣ α \text{compress}(x) = \text{sign}(x) \cdot |x|^\alpha compress(x)=sign(x)⋅∣x∣α
在这里, α \alpha α是压缩因子,通常取值在 0 < α < 1 0 < \alpha < 1 0<α<1 之间。较小的 α \alpha α值会导致更强的压缩效果,从而使得模型在训练时能够更好地学习小幅度信号的特征。通过这种方式,MC-MSE损失函数能够有效地提高模型在音频处理任务中的性能,尤其是在复杂的噪声环境中。它不仅改善了模型对小幅度信号的学习能力,还增强了模型的鲁棒性,使其在实际应用中表现得更加出色。
通过一个具体的例子来说明如何计算两个掩蔽之间的幅度幂律压缩均方误差(MC-MSE)。假设我们有两个掩蔽 M 1 M_1 M1 和 M 2 M_2 M2,它们的维度都是 3 × 3 3 \times 3 3×3(即3个时间帧和3个频率bin),并且我们选择压缩指数 p = 0.3 p = 0.3 p=0.3。
首先,我们对两个掩蔽应用幂律压缩。假设 M 1 M_1 M1 和 M 2 M_2 M2的值如下:
M 1 = [ 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 ] M_1 = \begin{bmatrix} 0.5 & 0.6 & 0.7 \\ 0.8 & 0.9 & 1.0 \\ 1.1 & 1.2 & 1.3 \end{bmatrix} M1= 0.50.81.10.60.91.20.71.01.3
M 2 = [ 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 ] M_2 = \begin{bmatrix} 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \\ 1.0 & 1.1 & 1.2 \end{bmatrix} M2= 0.40.71.00.50.81.10.60.91.2
应用幂律压缩 p = 0.3 p = 0.3 p=0.3后,我们得到:
M 1 p = [ 0. 5 0.3 0. 6 0.3 0. 7 0.3 0. 8 0.3 0. 9 0.3 1. 0 0.3 1. 1 0.3 1. 2 0.3 1. 3 0.3 ] M_1^p = \begin{bmatrix} 0.5^{0.3} & 0.6^{0.3} & 0.7^{0.3} \\ 0.8^{0.3} & 0.9^{0.3} & 1.0^{0.3} \\ 1.1^{0.3} & 1.2^{0.3} & 1.3^{0.3} \end{bmatrix} M1p= 0.50.30.80.31.10.30.60.30.90.31.20.30.70.31.00.31.30.3
M 2 p = [ 0. 4 0.3 0. 5 0.3 0. 6 0.3 0. 7 0.3 0. 8 0.3 0. 9 0.3 1. 0 0.3 1. 1 0.3 1. 2 0.3 ] M_2^p = \begin{bmatrix} 0.4^{0.3} & 0.5^{0.3} & 0.6^{0.3} \\ 0.7^{0.3} & 0.8^{0.3} & 0.9^{0.3} \\ 1.0^{0.3} & 1.1^{0.3} & 1.2^{0.3} \end{bmatrix} M2p= 0.40.30.70.31.00.30.50.30.80.31.10.30.60.30.90.31.20.3
接下来,我们计算两个压缩后的掩蔽之间的均方误差。具体地,对于每个元素,我们计算差的平方,然后对所有元素求平均。
L MC-MSE = 1 9 ( ( 0. 5 0.3 − 0. 4 0.3 ) 2 + ( 0. 6 0.3 − 0. 5 0.3 ) 2 + … + ( 1. 3 0.3 − 1. 2 0.3 ) 2 ) = 0.00135 L_{\text{MC-MSE}} = \frac{1}{9} \left( (0.5^{0.3} - 0.4^{0.3})^2 \\+ (0.6^{0.3} - 0.5^{0.3})^2 \\+ \ldots + (1.3^{0.3} - 1.2^{0.3})^2 \right) = 0.00135 LMC-MSE=91((0.50.3−0.40.3)2+(0.60.3−0.50.3)2+…+(1.30.3−1.20.3)2)=0.00135
import numpy as npdef calculate_mc_mse(M1, M2, p=0.3):compressed_M1 = M1 ** pcompressed_M2 = M2 ** pmse = np.mean((compressed_M1 - compressed_M2) ** 2)return mseM1 = np.array([[0.5, 0.6, 0.7], [0.8, 0.9, 1.0], [1.1, 1.2, 1.3]])
M2 = np.array([[0.4, 0.5, 0.6], [0.7, 0.8, 0.9], [1.0, 1.1, 1.2]])mc_mse = calculate_mc_mse(M1, M2, p=0.3)
print("MC-MSE:", mc_mse)
MC-MSE: 0.00135
三、融合损失函数
参考:AEC论文解读 – A Deep Hierarchical Fusion Network for Fullband Acoustic Echo Cancellation
结合 最优尺度不变信噪比(OSI-SNR) 和 幅度幂律压缩均方误差(MC-MSE) 的损失函数,可以通过超参数 γ \gamma γ 加权来形成最终的损失函数。根据您提供的公式,最终的损失计算公式可以表示为:
L = L OSI-SNR + γ L MC-MSE L = L_{\text{OSI-SNR}} + \gamma L_{\text{MC-MSE}} L=LOSI-SNR+γLMC-MSE
-
OSI-SNR 损失【方法 1】:
L OSI-SNR = 1 N ∑ i = 1 N Loss i = 1 N ∑ i = 1 N 1 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) + ϵ L_{\text{OSI-SNR}}= \frac{1}{N} \sum_{i=1}^{N} \text{Loss}_i = \frac{1}{N} \sum_{i=1}^{N} \frac{1}{10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) + \epsilon} LOSI-SNR=N1i=1∑NLossi=N1i=1∑N10log10(∥enoise,i∥2∥starget,i∥2)+ϵ1 -
MC-MSE 损失:
L MC-MSE = 1 N ∑ i = 1 N ( compress ( y i ) − compress ( y ^ i ) ) 2 L_{\text{MC-MSE}}= \frac{1}{N} \sum_{i=1}^{N} \left( \text{compress}(y_i) - \text{compress}(\hat{y}_i) \right)^2 LMC-MSE=N1i=1∑N(compress(yi)−compress(y^i))2 -
最终损失公式:
L = L OSI-SNR + γ ⋅ L MC-MSE = 1 N ∑ i = 1 N Loss i = 1 N ∑ i = 1 N 1 10 log 10 ( ∥ s target , i ∥ 2 ∥ e noise , i ∥ 2 ) + ϵ + γ ⋅ 1 N ∑ i = 1 N ( compress ( y i ) − compress ( y ^ i ) ) 2 L = L_{\text{OSI-SNR}} + \gamma \cdot L_{\text{MC-MSE}}= \frac{1}{N} \sum_{i=1}^{N} \text{Loss}_i \\= \frac{1}{N} \sum_{i=1}^{N} \frac{1}{10 \log_{10} \left( \frac{\| s_{\text{target}, i} \|^2}{\| e_{\text{noise}, i} \|^2} \right) + \epsilon} +\gamma \cdot\frac{1}{N} \sum_{i=1}^{N} \left( \text{compress}(y_i) - \text{compress}(\hat{y}_i) \right)^2 L=LOSI-SNR+γ⋅LMC-MSE=N1i=1∑NLossi=N1i=1∑N10log10(∥enoise,i∥2∥starget,i∥2)+ϵ1+γ⋅N1i=1∑N(compress(yi)−compress(y^i))2
- γ \gamma γ:需要调试的经验值。
- ϵ \epsilon ϵ:一个小常数,用于防止除以零的情况。
- 这个损失函数通过加权结合了 OSI-SNR 和 MC-MSE,能够同时考虑信号的重建质量和相似性。
- 通过调整 γ \gamma γ 的值,可以控制两种损失在最终损失中的相对重要性,从而优化模型的性能。
import numpy as np
def calculate_osi_snr_frame(target, estimated):num_bins, num_frames = target.shapeosi_snr_frames = np.zeros(num_frames)for frame in range(num_frames):dot_product = np.sum(target[:, frame] * estimated[:, frame])estimated_energy = np.sum(np.abs(estimated[:, frame]) ** 2)lambda_opt = estimated_energy / (dot_product + 1e-10) # 防止除以零target_adjusted = lambda_opt * target[:, frame]noise = estimated[:, frame] - target_adjustedtarget_energy = np.sum(np.abs(target_adjusted) ** 2)noise_energy = np.sum(np.abs(noise) ** 2)osi_snr_frames[frame] = 10 * np.log10(target_energy / (noise_energy + 1e-8))return osi_snr_frames
def mc_mse_loss(target, estimated, gamma=0.3):compressed_target = np.power(np.abs(target), gamma)compressed_estimated = np.power(np.abs(estimated), gamma)loss = np.mean((compressed_estimated - compressed_target) ** 2)return loss
def combined_loss(target, estimated, gamma=15):# 计算每一帧的 OSI-SNRosi_snr_frames = calculate_osi_snr_frame(target, estimated)# 计算 OSI-SNR 损失osi_snr_loss = np.mean(1 / (osi_snr_frames + 1e-10))print('osi_snr_loss:', osi_snr_loss)# 计算 MC-MSE 损失mc_mse_value = mc_mse_loss(target, estimated)print('mc_mse_value:', mc_mse_value)# 计算最终损失final_loss = osi_snr_loss + gamma * mc_mse_valuereturn final_loss
# 示例掩蔽矩阵 M1 和 M2
M1 = np.array([[0.5, 0.6, 0.7],[0.8, 0.9, 1.0],[1.1, 1.2, 1.3]])M2 = np.array([[0.4, 0.5, 0.6],[0.7, 0.8, 0.9],[1.0, 1.1, 1.2]])
# 计算最终损失
loss_value = combined_loss(M1, M2, gamma=15)
print(f'Final Loss: {loss_value:.5f}')osi_snr_loss: 0.033421230071106235
mc_mse_value: 0.0013543901266690674
Final Loss: 0.05374
相关文章:

语音增强的损失函数选择
一、最优尺度不变信噪比(OSISNR)损失函数 参考:论文解读 --Optimal scale-invariant signal-to-noise ratio and curriculum learning for monaural multi-spea 最优尺度不变信噪比(OSI-SNR)是一种用于评估信号质量…...
【python自动化六】UI自动化基础-selenium的使用
selenium是目前用得比较多的UI自动化测试框架,支持java,python等多种语言,目前我们就选用selenium来做UI自动化。 1.selenium安装 安装命令 pip install selenium2.selenium的简单使用 本文以chrome浏览器为例,配套selenium中c…...

【习题答案】让您的应用拥有领先的位置服务能力
判断题 1.在使用(逆)地理编码前,需要使用isGeocoderAvailable检查服务状态。 正确(True) 错误(False) 2.当同时配置定位场景和优先级策略时,会优先使用优先级策略。 正确(True) 错误(False) 单选题 1.获取精准定位需要申请哪个权…...

java中list和map区别
在Java中,List和Map是两种不同类型的集合接口,它们用于不同的场景并且具有不同的特性和用途。以下是List和Map的主要区别: 1. 数据结构 List:是一个有序的集合,允许重复元素。它实现了Collection接口,并且…...

java后端传时间戳给前端的三种方式
一. 后端传时间戳给前端的几种方式 使用System.currentTimeMillis() 这是最简单的方式,返回自1970年1月1日(UTC)以来的毫秒数,可以直接传递给前端。 long timestamp1 System.currentTimeMillis();使用java.time.Instant Java…...

【机器学习与数据挖掘实战】案例06:基于Apriori算法的餐饮企业菜品关联分析
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈机器学习与数据挖掘实战 ⌋ ⌋ ⌋ 机器学习是人工智能的一个分支,专注于让计算机系统通过数据学习和改进。它利用统计和计算方法,使模型能够从数据中自动提取特征并做出预测或决策。数据挖掘则是从大型数据集中发现模式、关联…...

oracle: create new database
用database configuration Assistant 引导创建数据库。记得给system,sys 设置自己的口令,便于添加新操作用户。 创建操作用户: -- 别加双引号,否则,无法用 create user geovindu identified by 888888; create user geovin identi…...

混合开发环境---使用编程AI辅助开发Qt
文章目录 [toc]1、说明2、演示视频 1、说明 新时代的浪潮早就已经来临,上不了船的人终将被抛弃,合理使用AI辅助开发、提升效率是大趋势 注意:不要被AI奴隶 合理使用AI辅助编程,十倍提升效率。 大部分的编程AI都有vs code插件&…...

Sigrity SystemSI仿真分析教程文件路径
为了方便读者能够快速上手和学会Sigrity SystemSI 的功能,将Sigrity SystemSI仿真分析教程专栏所有文章对应的实例文件上传至以下路径 https://download.csdn.net/download/weixin_54787054/90171488?spm1001.2014.3001.5503...

【YashanDB知识库】Oracle pipelined函数在YashanDB中的改写
本文内容来自YashanDB官网,原文内容请见 https://www.yashandb.com/newsinfo/7802940.html?templateId1718516 【问题分类】功能使用 【关键字】pipelined 【问题描述】 Oracle PL/SQL中包含pipelined函数的对象迁移到YashanDB会出现不兼容现象。 【问题原因分…...
【开发实战】QT5+ 工业相机 + OpenCV工作流集成演示
学习《OpenCV应用开发:入门、进阶与工程化实践》一书 做真正的OpenCV开发者,从入门到入职,一步到位! 概述 基于OpenCV工作流引擎SDK Qt5 海康工业相机实现了从图像采集到OpenCV工作流运行的完整流程。其中工业相机采图是一个单…...
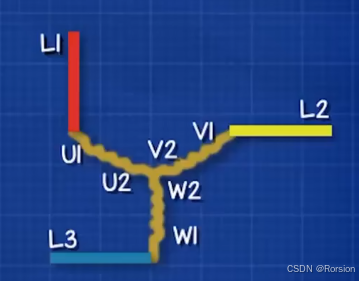
各种电机原理介绍
1,直流电机 (1)基本原理 直流电动机由直流电驱动电池或外部电源为其供电。在最简单的直流电动机中,定子为永磁体(即红蓝磁体外壳),转子是一个电磁体(即线圈),电流通过碳刷和一个换向器作用于转动的线圈。…...

深入了解 React:从入门到高级应用
深入了解 React:从入门到高级应用 React 是由 Facebook 开发并维护的一个开源 JavaScript 库,用于构建用户界面。自2013年发布以来,React 在前端开发领域迅速崛起,成为最受欢迎的 UI 构建工具之一。无论是小型的单页应用…...

Cglib代理简单案例
Cglib代理简单案例 前言: 1,实现对目标类的增强 2,源码后期补齐 步骤 1,添加cglib依赖 2,编写目标类,书写里面的方法 3,实现MethodInterceptor 接口,重写intercept方法 4ÿ…...

FreeMarker语法
1. 查找转移 <#function getSubSlot x > <#return (x) ? switch( "1", "L", "2", "R", "" )> </#function> 2. 转换数字 ?number ${mergedMap[placement.sequence].material.subs…...
)
DP动态规划(装箱问题)
# [NOIP2001 普及组] 装箱问题 ## 题目描述 有一个箱子容量为 $V$,同时有 $n$ 个物品,每个物品有一个体积。 现在从 $n$ 个物品中,任取若干个装入箱内(也可以不取),使箱子的剩余空间最小。输出这个最小值。…...

内网IP段介绍与汇总
IPV4内网段 IP地址段地址范围地址数量用途描述0.0.0.0/80.0.0.0–0.255.255.25516777216SoftwareCurrent network (only valid as source address).10.0.0.0/810.0.0.0–10.255.255.25516777216Private networkUsed for local communications within a private network.100.64…...

三、ubuntu18.04安装docker
1.使用默认ubuntu存储库安装docker 更新软件存储库 更新本地软件数据库确保可以访问最新版本。打开终端输入:sudo apt-get update 卸载旧版本的docker 建议继续之前卸载任何旧的docker软件。打开终端输入:sudo apt-get remove docker docker-engine …...
数据库与表空间
背景知识概述 数据库&模式 “实例/集簇”金仓是一个单实例管多库,把多库的集合叫做集簇,他们共用一个集簇目录,比如data目录下面里的子目录的数据文件。数据库里面有模式,在金仓里面模式是:据逻辑相关性对象的集…...

【CSS in Depth 2 精译_091】15.4:让 CSS 高度值过渡到自动高度 + 15.5:自定义属性的过渡设置(全新)+ 15.6:本章小结
当前内容所在位置(可进入专栏查看其他译好的章节内容) 第五部分 添加动效 ✔️【第 15 章 过渡】 ✔️ 15.1 状态间的由此及彼15.2 定时函数 15.2.1 定制贝塞尔曲线15.2.2 阶跃 15.3 非动画属性 15.3.1 不可添加动画效果的属性15.3.2 淡入与淡出 15.4 过…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
