OpenCV相机标定与3D重建(36)计算两幅图像之间基本矩阵(Fundamental Matrix)的函数findFundamentalMat()的使用
- 操作系统:ubuntu22.04
- OpenCV版本:OpenCV4.9
- IDE:Visual Studio Code
- 编程语言:C++11
算法描述
从两幅图像中的对应点计算基本矩阵。
cv::findFundamentalMat 是 OpenCV 中用于计算两幅图像之间基本矩阵(Fundamental Matrix)的函数。基本矩阵描述了两个未校准摄像机之间的几何关系,它在计算机视觉中用于立体视觉、运动结构恢复(Structure from Motion, SfM)、视觉里程计等任务。
函数原型
Mat cv::findFundamentalMat
(InputArray points1,InputArray points2,int method,double ransacReprojThreshold,double confidence,int maxIters,OutputArray mask = noArray()
) 参数
- 参数points1:来自第一幅图像的 N 个点数组。点的坐标应该是浮点数(单精度或双精度)。
- 参数points2:第二幅图像的点数组,与 points1 具有相同的大小和格式。
- 参数method:计算基本矩阵的方法。
- FM_7POINT:用于7点算法。N=7
- FM_8POINT:用于8点算法。N≥8
- FM_RANSAC:用于RANSAC算法。N≥8
- FM_LMEDS:用于最小中值法(LMedS)算法。N≥8
- 参数ransacReprojThreshold:仅用于 RANSAC 的参数。它是点到极线的最大距离(以像素为单位),超过该距离的点被认为是离群点,并不用于计算最终的基本矩阵。根据点定位的准确性、图像分辨率和图像噪声,它可以设置为1-3等。
- 参数confidence:仅用于 RANSAC 和 LMedS 方法的参数。它指定了估计矩阵正确的期望置信水平(概率)。
- 参数[out] mask:可选输出掩码。
- 参数maxIters:稳健方法的最大迭代次数。
说明
极几何由以下方程描述:
[ p 2 ; 1 ] T F [ p 1 ; 1 ] = 0 [p_2; 1]^T F [p_1; 1] = 0 [p2;1]TF[p1;1]=0
其中 F 是基本矩阵,p1和p2分别是第一幅和第二幅图像中的对应点。
该函数使用上述列出的四种方法之一来计算基本矩阵,并返回找到的基本矩阵。通常只找到一个矩阵。但在7点算法的情况下,该函数可能返回多达3个解(一个 9×3 矩阵,按顺序存储所有3个矩阵)。
// Example. Estimation of fundamental matrix using the RANSAC algorithm
int point_count = 100;
vector<Point2f> points1(point_count);
vector<Point2f> points2(point_count);
// initialize the points here ...
for( int i = 0; i < point_count; i++ )
{points1[i] = ...;points2[i] = ...;
}
Mat fundamental_matrix =findFundamentalMat(points1, points2, FM_RANSAC, 3, 0.99);
代码示例
#include <iostream>
#include <opencv2/opencv.hpp>using namespace cv;
using namespace std;int main( int argc, char** argv )
{// 创建虚拟的匹配点数据(假设我们有8对匹配点)vector< Point2f > points1 = { Point2f( 154.0f, 38.0f ), Point2f( 285.0f, 176.0f ), Point2f( 279.0f, 238.0f ), Point2f( 276.0f, 284.0f ),Point2f( 273.0f, 342.0f ), Point2f( 267.0f, 397.0f ), Point2f( 262.0f, 446.0f ), Point2f( 254.0f, 495.0f ) };vector< Point2f > points2 = { Point2f( 149.0f, 49.0f ), Point2f( 280.0f, 187.0f ), Point2f( 274.0f, 249.0f ), Point2f( 271.0f, 295.0f ),Point2f( 268.0f, 353.0f ), Point2f( 262.0f, 408.0f ), Point2f( 257.0f, 457.0f ), Point2f( 249.0f, 506.0f ) };// 定义输出的基本矩阵和掩码Mat fundamentalMatrix, mask;// 使用 RANSAC 方法计算基本矩阵fundamentalMatrix = findFundamentalMat( points1, points2,FM_RANSAC, // 使用RANSAC方法1.0, // 点到极线的最大重投影误差0.99, // 置信水平2000, // 最大迭代次数mask ); // 输出掩码// 打印结果cout << "Fundamental Matrix:\n" << fundamentalMatrix << endl;// 打印哪些点被认为是内点cout << "Inliers mask:\n";for ( size_t i = 0; i < mask.total(); ++i ){if ( mask.at< uchar >( i ) ){cout << "Point " << i + 1 << " is an inlier." << endl;}else{cout << "Point " << i + 1 << " is an outlier." << endl;}}return 0;
}
运行结果
Fundamental Matrix:
[-3.247212965698772e-20, -0.0008949509319799827, 0.704568065615863;0.0008949509319799836, 3.892534466973619e-19, 0.229349120734492;-0.7144125258676433, -0.2338238753943923, 1]
Inliers mask:
Point 1 is an inlier.
Point 2 is an inlier.
Point 3 is an inlier.
Point 4 is an inlier.
Point 5 is an inlier.
Point 6 is an inlier.
Point 7 is an inlier.
Point 8 is an inlier.
相关文章:
计算两幅图像之间基本矩阵(Fundamental Matrix)的函数findFundamentalMat()的使用)
OpenCV相机标定与3D重建(36)计算两幅图像之间基本矩阵(Fundamental Matrix)的函数findFundamentalMat()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 从两幅图像中的对应点计算基本矩阵。 cv::findFundamentalMat 是 OpenCV 中用于计算两幅图像之间基本矩阵(Fundamental Matrix&#…...
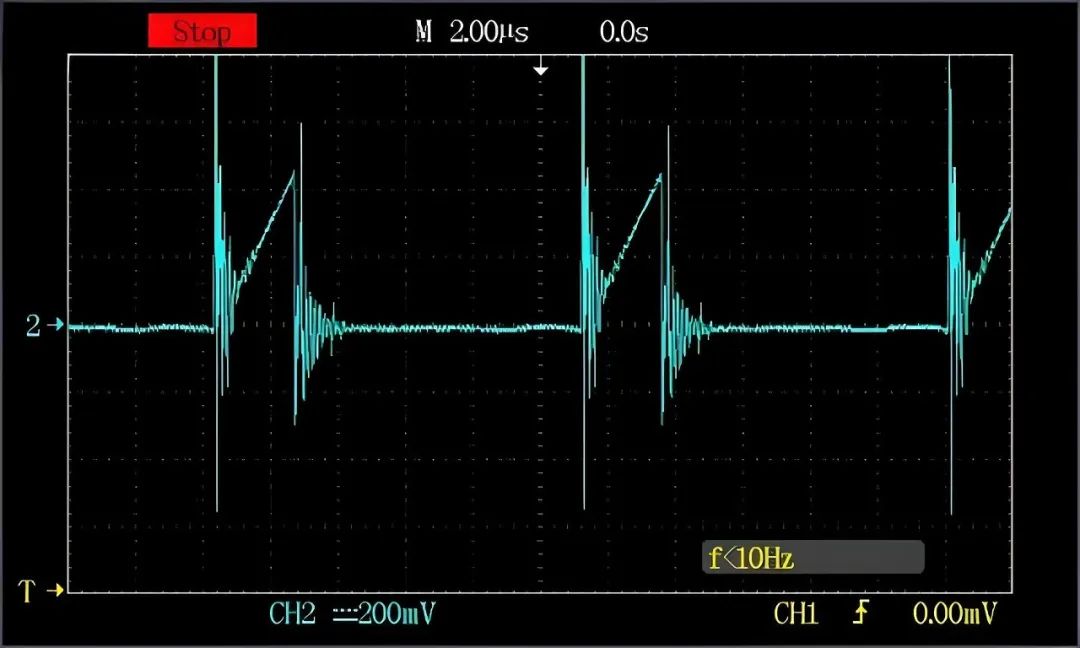
ZLG嵌入式笔记 | 电源设计避坑(上)
产品上量后,通常都会有降成需求。多年来,接触过不少产品降成案例,在电源上下刀过猛,引发了产品偶发性问题,带来了很不好的负面影响。本文将对这些案例进行总结,提供电源设计参考,确保产品降成不…...

.NET能做什么?全面解析.NET的应用领域
.NET 是由微软开发的一个开源、跨平台的开发框架。它不仅支持构建各种应用程序,还能运行在不同的操作系统上,包括 Windows、Linux 和 macOS。自从 .NET Core 的推出,.NET 成为了一个现代化的开发平台,能够满足企业和开发者日益多样…...

初始JavaEE篇 —— 网络原理---传输层协议:深入理解UDP/TCP
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程程(ಥ_ಥ)-CSDN博客 所属专栏:JavaEE 目录 UDP协议 参数解析: 校验和的计算 TCP协议 参数解析: 确认应答机制 超时重传 连接管理 三次握…...

企业如何搭建安全的跨网文件安全交换管理系统
在数字化转型的浪潮中,企业对数据的安全性和流动性提出了前所未有的高要求。特别是在网络隔离的情况下,如何实现跨网的安全、高效的文件交换成为了众多企业迫切需要解决的问题。 这不仅是技术上的挑战,还涉及到企业内部管理流程的优化和安全策…...

2023 年 12 月青少年软编等考 C 语言四级真题解析
目录 T1. 移动路线T2. 公共子序列T3. 田忌赛马T4. 宠物小精灵之收服 T1. 移动路线 此题为 2021 年 12 月四级第一题原题,见 2021 年 12 月青少年软编等考 C 语言四级真题解析中的 T1。 T2. 公共子序列 此题为 2022 年 3 月四级第四题原题,见 2022 年 …...
)
GDPU Vue前端框架开发 期末赛道出勇士篇(更新ing)
记住,年底陪你跨年的不会仅是方便面跟你的闺蜜,还有孑的笔记。 选择题 1.下列选项用于设置Vue.js页面视图的元素是()。 A. Template B. script C. style D. title 2.下列选项中能够定义Vuejs根实例对象的元素是(&…...

老旧小区用电安全保护装置#限流式防火保护器参数介绍#
摘要 随着居民住宅区用电负荷的增加,用电安全问题日益突出,火灾隐患频繁发生。防火限流式保护器作为一种新型电气安全设备,能够有效预防因电气故障引发的火灾事故。本文介绍了防火限流式保护器的工作原理、技术特点及其在居民住宅区用电系统…...

7.C语言 宏(Macro) 宏定义,宏函数
目录 宏定义 宏函数 1.注释事项 2.注意事项 宏(Macro)用法 常量定义 简单函数实现 类型检查 条件编译 宏函数计算参数个数 宏定义进行类型转换 宏定义进行位操作 宏定义进行断言 总结 宏定义 #include "stdio.h" #include "string.h" #incl…...

4.系统学习-集成学习
集成学习 前言Bias and Variance过拟合(overfitting)与欠拟合(underfitting)集成学习为什么有效?Blending 模型集成Stakcing 模型集成Bagging模型集成Bagging 模型集成算法流程:Boosting模型集成作业 前言 …...

Max AI prompt2:
1,prompt1——总体概览 “请根据以下指导原则撰写文献解读,特别关注作者的研究思路和方法论: 1. 研究背景与目的: 概述文章研究的背景,明确研究的主要目的和研究问题。 2. 研究思路: 详细描述作者如何构建…...

[Unity Shader][图形渲染]【游戏开发】 Shader数学基础8 - 齐次坐标
在计算机图形学中,齐次坐标是一种方便计算和表示几何变换的方式。通过将三维空间中的 33矩阵扩展为 44的形式,可以统一表示平移、旋转、缩放等几何变换操作。在本篇文章中,我们将详细解析齐次坐标的定义及其在图形变换中的应用。 什么是齐次坐标? 齐次坐标的核心思想是通过…...

挑战一个月基本掌握C++(第十二天)了解命名空间,模板,预处理器
一 命名空间 假设这样一种情况,当一个班上有两个名叫 Zara 的学生时,为了明确区分它们,我们在使用名字之外,不得不使用一些额外的信息,比如他们的家庭住址,或者他们父母的名字等等。 同样的情况也出现在 …...

python实现根据搜索关键词爬取某宝商品信息
当程序打开淘宝登陆页面后,需要快速手动登录淘宝,如果服务报错,需要重新登录! pip安装库 pip install pyquery pip install selenium pip install openpyxl # 代码说明:代码功能: 基于ChromeDriver爬取tao…...

Posison Distribution
泊松分布 (Poisson Distribution) 泊松分布是概率论中的一个重要离散分布,描述单位时间或单位空间内随机事件发生的次数,假设事件是独立的且平均发生率是已知的。 定义 泊松分布的概率质量函数 (PMF) 为: P ( X k ) λ k e − λ k ! , …...

2024年最新多目标优化算法:多目标麋鹿群优化算法(MOEHO)求解ZDT1-ZDT4,ZDT6及工程应用---盘式制动器设计,提供完整MATLAB代码
一、麋鹿群优化算法 麋鹿群优化算法(Elephant Herding Optimization,EHO)是2024年提出的一种启发式优化算法,它的灵感来自麋鹿群的繁殖过程。麋鹿有两个主要的繁殖季节:发情和产犊。在发情季节,麋鹿群分裂…...

使用Webpack构建微前端应用
英文社区对 Webpack Module Federation 的响应非常热烈,甚至被誉为“A game-changer in JavaScript architecture”,相对而言国内对此热度并不高,这一方面是因为 MF 强依赖于 Webpack5,升级成本有点高;另一方面是国内已…...

Apache RocketMQ 5.1.3安装部署文档
官方文档不好使,可以说是一坨… 关键词:Apache RocketMQ 5.0 JDK 17 废话少说,开整。 1.版本 官网地址,版本如下。 https://rocketmq.apache.org/download2.配置文件 2.1namesrv端口 在ROCKETMQ_HOME/conf下 新增namesrv.pro…...
垃圾回收器的具体流程)
CMS(Concurrent Mark Sweep)垃圾回收器的具体流程
引言 CMS(Concurrent Mark Sweep)收集器是Java虚拟机中的一款并发收集器,其设计目标是最小化停顿时间,非常适合于对响应时间敏感的应用。与传统的串行或并行收集器不同,CMS能够尽可能地让垃圾收集线程与用户线程同时运…...

【Linux】Socket编程-UDP构建自己的C++服务器
🌈 个人主页:Zfox_ 🔥 系列专栏:Linux 目录 一:🔥 UDP 网络编程 🦋 接口讲解🦋 V1 版本 - echo server🦋 V2 版本 - DictServer🦋 V3 版本 - 简单聊天室 二&a…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
深入理解 C++ 左值右值、std::move 与函数重载中的参数传递
在 C 编程中,左值和右值的概念以及std::move的使用,常常让开发者感到困惑。特别是在函数重载场景下,如何合理利用这些特性来优化代码性能、确保语义正确,更是一个值得深入探讨的话题。 在开始之前,先提出几个问题&…...
