信号的时域截断——频谱泄漏——光晕效应
在时域信号中,如果对一个包含不连续点的信号进行截断,即使用有限个样本点来表示原本无限长或更长的信号,那么在频域中这相当于对信号进行了乘以一个矩形窗的操作。这种操作会导致原信号频谱与矩形窗的频谱卷积,从而在频域中引入额外的频率成分,这就是所谓的“频谱泄漏”(Spectral Leakage)。
频谱泄漏(Spectral Leakage)是指在对一个非周期信号或周期但长度与分析窗口不匹配的信号进行离散傅里叶变换(DFT)时,信号的能量不再集中在原来的频率位置,而是扩散到周围的频率上。这种现象主要是由于信号在时域中被截断所引起的。
同时,在时域中,这种截断也会导致Gibbs现象的发生,即在信号的不连续点附近会出现振荡,这些振荡的峰值不会随着采样点数目的增加而减少。
数学解释
假设有一个连续时间信号 x ( t ) x(t) x(t),其傅里叶变换为 X ( f ) X(f) X(f)。当我们对该信号进行采样,得到离散时间信号 x [ n ] = x ( n T s ) x[n] = x(nT_s) x[n]=x(nTs),其中 T s T_s Ts是采样间隔, f s = 1 / T s f_s = 1/T_s fs=1/Ts是采样频率。然后我们对 N N N个采样点进行 DFT,得到离散频谱 X [ k ] X[k] X[k]。
1. 理想情况下的 DFT
如果 x ( t ) x(t) x(t)是一个周期信号,并且采样点数 N N N恰好等于信号的一个完整周期,则 DFT 可以完美地表示信号的频谱。此时,DFT 的定义为:
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − j 2 π k n / N X[k] = \sum_{n=0}^{N-1} x[n] e^{-j 2 \pi k n / N} X[k]=n=0∑N−1x[n]e−j2πkn/N
2. 实际情况下的 DFT
然而,大多数情况下,信号不是严格周期的,或者采样点数 N N N不等于信号的一个完整周期。在这种情况下,信号在时域中被一个矩形窗 w [ n ] w[n] w[n]截断,即:
x N [ n ] = x [ n ] ⋅ w [ n ] x_N[n] = x[n] \cdot w[n] xN[n]=x[n]⋅w[n]
其中,矩形窗 w [ n ] w[n] w[n]定义为:
w [ n ] = { 1 if 0 ≤ n < N 0 otherwise w[n] = \begin{cases} 1 & \text{if } 0 \leq n < N \\ 0 & \text{otherwise} \end{cases} w[n]={10if 0≤n<Notherwise
因此,实际的 DFT 变为:
X N [ k ] = ∑ n = 0 N − 1 x [ n ] w [ n ] e − j 2 π k n / N X_N[k] = \sum_{n=0}^{N-1} x[n] w[n] e^{-j 2 \pi k n / N} XN[k]=n=0∑N−1x[n]w[n]e−j2πkn/N
根据傅里叶变换的性质,时域中的乘积对应于频域中的卷积。因此,实际的频谱 X w ( f ) X_w(f) Xw(f)可以表示为:
X w ( f ) = X ( f ) ∗ W ( f ) X_w(f) = X(f) * W(f) Xw(f)=X(f)∗W(f)
其中, W ( f ) W(f) W(f)是矩形窗的傅里叶变换,即:
W ( f ) = sin ( π f N ) sin ( π f ) W(f) = \frac{\sin(\pi f N)}{\sin(\pi f)} W(f)=sin(πf)sin(πfN)
这个函数被称为 sinc 函数,其主瓣宽度为 2 N \frac{2}{N} N2Hz,旁瓣高度逐渐减小但始终存在。
频谱泄漏的影响
由于 W ( f ) W(f) W(f)的主瓣和旁瓣,实际的频谱 X w ( f ) X_w(f) Xw(f)会受到以下影响:
- 主瓣宽度:主瓣越宽,信号的能量就越分散,导致分辨率降低。
- 旁瓣高度:旁瓣的存在会导致相邻频率成分之间的干扰,使得频谱中的尖峰变得模糊。


增加数据长度——提高频率分辨率
相关文章:

信号的时域截断——频谱泄漏——光晕效应
在时域信号中,如果对一个包含不连续点的信号进行截断,即使用有限个样本点来表示原本无限长或更长的信号,那么在频域中这相当于对信号进行了乘以一个矩形窗的操作。这种操作会导致原信号频谱与矩形窗的频谱卷积,从而在频域中引入额…...
)
【Linux编程】TcpServer 类的设计与实现:构建高性能的 TCP 服务器(二)
TcpServer 类的设计与实现:构建高性能的 TCP 服务器 在现代网络编程中,构建一个高效、稳定的 TCP 服务器是许多网络应用的基础。本文将详细介绍一个基于 C 的 TcpServer 类的设计与实现,该类提供了创建 TCP 服务器、处理客户端连接、数据传输…...

Mono里运行C#脚本8—mono_image_storage_open打开EXE文件
Mono里运行C#脚本8—mono_image_storage_open打开EXE文件 前面分析哈希表的实现,以及文件打开的底层函数,还有保存到HASH表里的数据结构。 static MonoImageStorage * mono_image_storage_open (const char *fname) { char *key = NULL; key = mono_path_resolve_symlinks…...

XMLHttpRequest的基础知识
get请求 const xml new XMLHttpRequest(); xml.open("GET", "https://jsonplaceholder.typicode.com/todos/1", true); xml.onreadystatechange function () {if (xml.readyState 4 && xml.status 200) {console.log(xml.responseText);} }…...

力扣矩阵-算法模版总结
lc-73.矩阵置零-(时隔14天)-12.27 思路:(23min22s) 1.直接遍历遇0将行列设0肯定不行,会影响后续判断,题目又要求原地算法,那么进一步考虑是否可以将元素为0,其行列需要设为0的位置给存储下来,最后再遍历根据…...
如何在短时间内读懂复杂的英文文献?
当我们拿起一篇文献开始阅读时,就像是打开了一扇通往未知世界的大门。但别急着一头扎进去,咱们得像个侦探一样,带着疑问去探险。毕竟,知识的海洋深不可测,不带点“装备”怎么行?今天就聊聊,平时…...

基于aspose.words组件的word bytes转pdf bytes,去除水印和解决linux中文乱码问题
详情见 https://preferdoor.top/archives/ji-yu-aspose.wordszu-jian-de-word-byteszhuan-pdf-bytes...

Bert中文文本分类
这是一个经典的文本分类问题,使用google的预训练模型BERT中文版bert-base-chinese来做中文文本分类。可以先在Huggingface上下载预训练模型备用。https://huggingface.co/google-bert/bert-base-chinese/tree/main 我使用的训练环境是 pip install torch2.0.0; pi…...

【深度学习】Java DL4J基于 CNN 构建车辆识别与跟踪模型
🧑 博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/?__c1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,精通Java编…...
介绍)
【C#】C#打印当前时间以及TimeSpan()介绍
1. C#打印当前时间 string currentDate DateTime.Now.ToString("yyyy-MM-dd HH:mm:ss.fff");Console.WriteLine(currentDate);2. TimeSpan()介绍 TimeSpan(long ticks)的单位是100ns //500ms new TimeSpan(10*1000*500);参考: C#-TimeSpan-计算时间差...

【Linux 网络 (五)】Tcp/Udp协议
Linux 网络 一前言二、Udp协议1)、Udp协议特点2)、Udp协议格式3)、Udp报文封装和解包过程4)、UDP的缓冲区 三、TCP协议1)、TCP协议特点2)、TCP协议格式1、4位首部长度、源端口、目的端口2、16位窗口大小3、…...

多旋翼无人机理论 | 四旋翼动力学数学模型与Matlab仿真
多旋翼无人机理论 | 四旋翼动力学数学模型与Matlab仿真 力的来源数学模型数学模型总结Matlab 仿真 力的来源 无人机的动力系统:电调-电机-螺旋桨 。 给人最直观的感受就是 电机带动螺旋桨转,产生升力。 螺旋桨旋转产生升力的原因,在很多年…...

Vue3项目中引入TailwindCSS(图文详情)
Vue3项目中引入TailwindCSS(图文详细) Tailwind CSS 是一个实用工具优先的 CSS 框架,提供丰富的低级类(如 text-center、bg-blue-500),允许开发者通过组合这些类快速构建自定义设计,而无需编写…...
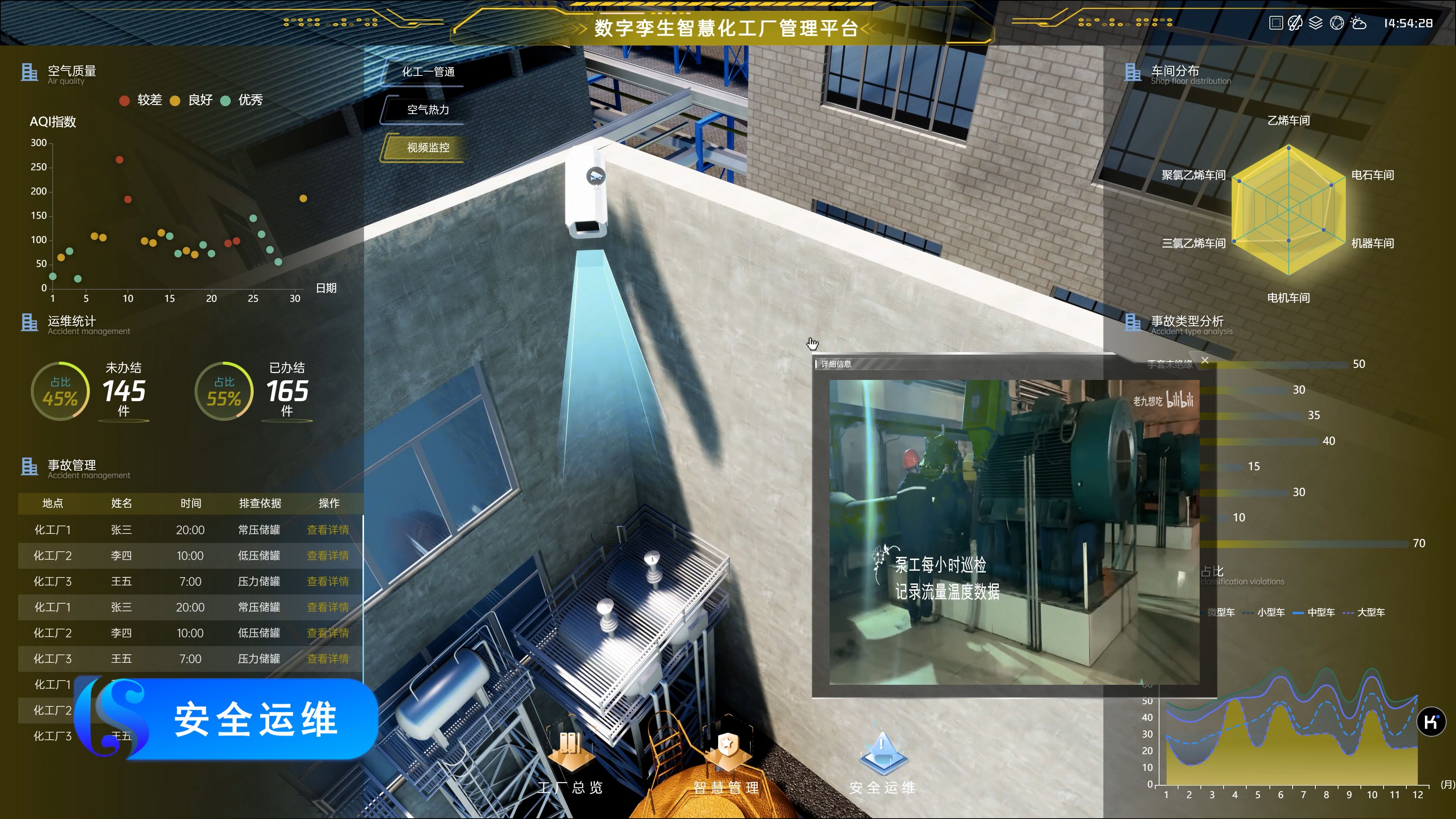
【开源项目】数字孪生化工厂—开源工程及源码
飞渡科技数字孪生化工厂管理平台,基于自研孪生引擎,将物联网IOT、人工智能、大数据、云计算等技术应用于化工厂,为化工厂提供实时数据分析、工艺优化、设备运维等功能,助力提高生产效率以及提供安全保障。 通过可视化点位标注各厂…...

咨询团队如何通过轻量型工具优化项目管理和提高团队协作效率?
引言 在咨询行业,项目的复杂性和多样性往往意味着团队成员需要协同工作、迅速适应客户需求的变化并且在较短的时间内交付高质量的成果。对于咨询团队来说,选择一个适合的项目管理工具,不仅能够提高工作效率,还能促进团队的协作、…...

javaWeb开发
Java Web开发作为软件开发领域的一个重要分支,已经历经数十年的发展,并凭借其强大的跨平台能力、丰富的生态系统以及高度的安全性,成为构建企业级应用的首选技术之一。以下是对Java Web开发的详细解析: 一、Java Web开发的基本概…...

如何在 Vue 中处理 API 请求?
在 Vue.js 中处理 API 请求是构建动态、交互式 Web 应用程序的核心部分。为了有效地与后端服务器通信,Vue 生态系统提供了多种方式来发起和管理 API 请求。以下是几种常见的方法和最佳实践: 1. 使用 Axios Axios 是一个基于 Promise 的 HTTP 客户端&am…...

基于Debian的Linux发行版的包管理工具
基于Debian的Linux发行版中除了apt和apt-get之外,还有以下几种包管理工具: dpkg:这是Debian系发行版中最基础的包管理工具,专门用于安装、卸载和查询.deb包。与高级包管理器不同,dpkg不自动解决包的依赖关系࿰…...
)
2022年国家公考《申论》题(行政执法)
2022年国家公考《申论》题(行政执法) 材料一 新型冠状病毒肺炎疫情发生后,党中央、国务院出台了一系列支持企业发展的惠企政策。N市积极落实各项惠企政策,不断优化营商环境,推动区域经济高质量跨越式发展。 “当时…...

贪心算法(常见贪心模型)
常见贪心模型 简单排序模型 最小化战斗力差距 题目分析: #include <bits/stdc.h> using namespace std;const int N 1e5 10;int n; int a[N];int main() {// 请在此输入您的代码cin >> n;for (int i 1;i < n;i) cin >> a[i];sort(a1,a1n);…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
