【递归与回溯深度解析:经典题解精讲(中篇)】—— LeetCode
文章目录
- 组合
- 目标和
- 组合总和
- 字母大小写全排序
- 优美的排列
- N皇后
组合

思路:回溯算法
- 问题要求从 1 到 n 中选出 k 个数的所有组合。
使用回溯算法递归构造解。
每次递归时,记录当前的组合路径,当组合长度达到 k 时,将其加入结果集。
剪枝优化:在递归过程中,如果当前选择的起点到 n 不够 k 个数,就停止递归。
class Solution
{vector<vector<int>> ret; // 用于存储最终的所有组合结果vector<int> path; // 用于存储当前正在构建的组合int n, k; // n 表示范围 [1, n],k 表示组合的大小public:vector<vector<int>> combine(int _n, int _k) {n = _n; // 初始化 nk = _k; // 初始化 kdfs(1); // 从数字 1 开始进行深度优先搜索return ret; // 返回所有的组合结果}// 深度优先搜索函数,用于生成所有的组合void dfs(int pos){// 如果当前组合的大小等于 k,则将该组合加入结果集if(k == path.size()){ret.push_back(path); // 将当前组合存储到结果集中return; // 返回,结束当前递归分支}// 从当前数字 pos 开始,尝试加入到组合中for(int i = pos; i <= n; i++){path.push_back(i); // 将当前数字加入到组合中dfs(i + 1); // 递归调用,处理下一个数字,确保数字不会重复path.pop_back(); // 回溯:移除最后加入的数字,尝试其他可能性}}
};
目标和

回溯:
- 通过正负号的分配来形成目标和,尝试所有可能的组合。
如果找到一种方式满足条件,计数+1。
class Solution
{int ret, aim; // `ret` 用于存储满足条件的方案总数,`aim` 是目标值public:int findTargetSumWays(vector<int>& nums, int target) {aim = target; // 初始化目标值ret = 0; // 初始化方案数dfs(nums, 0, 0); // 从索引 0 开始递归搜索,初始路径和为 0return ret; // 返回满足条件的方案数}// 深度优先搜索函数,用于枚举所有可能的路径和void dfs(vector<int>& nums, int pos, int path){// 如果已经遍历到数组末尾,检查路径和是否等于目标值if(pos == nums.size()){if(path == aim) ret++; // 如果路径和等于目标值,则方案数加 1return; // 返回,结束当前递归分支}// 选择将当前数字加到路径和dfs(nums, pos + 1, path + nums[pos]);// 选择将当前数字减到路径和dfs(nums, pos + 1, path - nums[pos]);}
};
组合总和

思路:回溯算法
- 使用回溯方法,试图从给定的数字中选出若干个数(可重复)使其和为目标值。
在递归过程中:
当前路径的总和如果大于目标值,停止搜索。
如果总和等于目标值,将当前路径加入结果。
每次递归时从当前数字开始,避免重复路径。
class Solution
{int aim; // 目标和vector<vector<int>> ret; // 存储所有满足条件的组合vector<int> path; // 存储当前路径(正在构建的组合)public:vector<vector<int>> combinationSum(vector<int>& nums, int target) {aim = target; // 设置目标和dfs(nums, 0, 0); // 从索引 0 开始深度优先搜索,当前和为 0return ret; // 返回所有符合条件的组合}// 深度优先搜索函数void dfs(vector<int>& nums, int pos, int sum){// 如果当前和等于目标值,将当前组合加入结果集if(sum == aim){ret.push_back(path); // 将当前路径(组合)存入结果集return; // 返回,结束当前递归分支}// 如果当前和超过目标值,或索引超出数组范围,则返回if(sum > aim || pos == nums.size()) return;// 从当前索引 `pos` 开始,尝试每个数字for(int i = pos; i < nums.size(); i++){path.push_back(nums[i]); // 将当前数字加入到路径中dfs(nums, i, sum + nums[i]); // 递归调用,允许重复选择当前数字path.pop_back(); // 回溯:移除最后一个加入的数字,尝试其他可能性}}
};
字母大小写全排序

思路:回溯算法
- 遍历字符串,每遇到一个字母字符,就有两种选择(小写或大写)。
使用递归构造所有可能的字符串路径:
对于每个字符,选择原字符或大小写转换后的字符加入路径。
遇到数字时,直接加入路径。
当遍历到字符串末尾时,将路径加入结果集。
class Solution
{vector<string> ret; // 用于存储所有满足条件的字符串组合string path; // 当前正在构建的路径(部分字符串)public:vector<string> letterCasePermutation(string s) {dfs(s, 0); // 从字符串的第 0 个字符开始深度优先搜索return ret; // 返回所有可能的组合结果}// 深度优先搜索函数void dfs(string& s, int pos){// 如果当前处理位置等于字符串长度,说明路径构造完成if(pos == s.size()){ret.push_back(path); // 将路径加入结果集return; // 返回,结束当前递归分支}char ch = s[pos];// 情况 1:不改变当前字符,直接加入路径path.push_back(ch);dfs(s, pos + 1); // 递归处理下一个字符path.pop_back(); // 回溯,移除当前字符// 情况 2:改变当前字符的大小写if(ch < '0' || ch > '9') // 如果当前字符不是数字,尝试改变大小写{char tmp = change(ch); // 改变字符大小写path.push_back(tmp); // 将改变后的字符加入路径dfs(s, pos + 1); // 递归处理下一个字符path.pop_back(); // 回溯,移除改变后的字符}}// 辅助函数:改变字符的大小写char change(char ch){if(ch <= 'z' && ch >= 'a') ch -= 32; // 小写转大写else ch += 32; // 大写转小写return ch;}
};
优美的排列

思路:回溯+剪枝
- 使用回溯法,尝试将数字放入数组中。
每次递归时,判断当前数字是否满足条件(能被当前位置整除或能整除当前位置)。
剪枝优化:如果当前排列不符合条件,提前停止递归。
class Solution
{int ret; // 用于记录满足条件的排列方案数bool check[16]; // 用于记录数字是否被使用过(数组下标从 1 开始)public:int countArrangement(int n) {dfs(n, 1); // 从位置 1 开始深度优先搜索return ret; // 返回最终的方案数}// 深度优先搜索函数void dfs(int n, int pos){// 递归终止条件:如果当前位置超出 n,说明排列完成if(pos == n + 1){ret++; // 当前排列满足条件,计数加 1return; // 返回,结束当前递归分支}// 尝试将每个数字放在当前的位置for(int i = 1; i <= n; i++){// 如果数字 i 尚未被使用,且满足题目中的条件if(!check[i] && (pos % i == 0 || i % pos == 0)){check[i] = true; // 标记数字 i 已被使用dfs(n, pos + 1); // 递归处理下一个位置check[i] = false; // 回溯:取消数字 i 的使用状态}}}
};
N皇后

思路:回溯+剪枝
- 使用回溯法尝试将 N 个皇后放置到 N×N 棋盘上。
在递归过程中,每一行尝试放置一个皇后:
检查当前列、主对角线、副对角线是否已被占用。
剪枝优化:利用标志数组记录列、主对角线、副对角线是否被占用,避免重复检查。
当所有行都放置完成时,将当前结果加入结果集。
class Solution
{bool checkCol[10], checkdig1[20], checkdig2[20]; // 分别记录列、主对角线、副对角线是否被占用vector<vector<string>> ret; // 存储所有符合条件的棋盘配置vector<string> path; // 当前棋盘状态int n; // 棋盘的大小public:vector<vector<string>> solveNQueens(int _n) {n = _n; // 初始化棋盘大小path.resize(n); // 初始化棋盘状态for(int i = 0; i < n; i++)path[i].append(n, '.'); // 将每一行初始化为 `n` 个 '.'(表示空位置)dfs(0); // 从第 0 行开始深度优先搜索return ret; // 返回所有符合条件的棋盘配置}// 深度优先搜索函数void dfs(int row){// 递归终止条件:如果已经处理到第 n 行,说明所有皇后都已放置完成if(row == n){ret.push_back(path); // 将当前棋盘状态加入结果集return; // 返回,结束当前递归分支}// 遍历当前行的每一列,尝试放置皇后for(int col = 0; col < n; col++){// 检查当前列、主对角线、副对角线是否被占用if(!checkCol[col] && !checkdig1[row - col + n] && !checkdig2[row + col]){// 放置皇后,更新棋盘状态和限制条件path[row][col] = 'Q'; // 在 (row, col) 放置皇后checkCol[col] = checkdig1[row - col + n] = checkdig2[row + col] = true; // 标记当前位置dfs(row + 1); // 递归处理下一行// 回溯:移除皇后,恢复棋盘状态和限制条件path[row][col] = '.'; // 移除 (row, col) 的皇后checkCol[col] = checkdig1[row - col + n] = checkdig2[row + col] = false; // 取消标记}}}
};
相关文章:

【递归与回溯深度解析:经典题解精讲(中篇)】—— LeetCode
文章目录 组合目标和组合总和字母大小写全排序优美的排列N皇后 组合 思路:回溯算法 问题要求从 1 到 n 中选出 k 个数的所有组合。 使用回溯算法递归构造解。 每次递归时,记录当前的组合路径,当组合长度达到 k 时,将其加入结果集…...

01.HTTPS的实现原理-HTTPS的概念
01.HTTPS的实现原理-HTTPS的概念 简介1. HTTPS的概念和安全性2. HTTPS的实现原理3. HTTPS和HTTP的区别4. OSI七层协议模型5. SSL和TLS的区别 简介 该系列文章主要讲述了HTTPS协议与HTTP协议的区别,以及HTTPS如何实现安全传输。内容分为三部分:HTTPS的实…...

一文详解MacOS+CLion——构建libtorch机器学习开发环境
对于希望在本地环境中进行深度学习开发的开发者来说,配置合适的工具链是至关重要的一步。本文旨在帮助您在 macOS 操作系统上,利用 CLion IDE 和 PyTorch 的 C依赖库——libtorch,快速搭建起一个高效的开发环境。这里我们将一步步地讲解如何下…...

【LeetCode 面试经典150题】详细题解之哈希表篇
【LeetCode 面试经典150题】详细题解之哈希表篇 1 哈希表的基础1.1 基础概念及实现1.2.1 哈希表的工作原理1.2.2 705.设计哈希集合1.2.3 706.设计哈希映射 1.2 HashMap相关1.2.1 基本操作1.2.2 遍历 1.3 Hashtable1.4 LinkedHashMap1.5 HashSet**1.5.1基本特性**1.5.2 基本方法…...

linux socket编程之udp_dict_serve服务端--引入配置文件
注意:本篇博客只是对上一篇博客功能的增加 1.创建配置文件(翻译) Dict.txt apple: 苹果 banana: 香蕉 cat: 猫 dog: 狗 book: 书 pen: 笔 happy: 快乐的 sad: 悲伤的 run: 跑 jump: 跳 teacher: 老师 student: 学生 car: 汽车 bus: 公交车 love: 爱 hate: 恨 hell…...
)
selenium学习笔记(二)
文章目录 前言设计模式POMPOM概念POM优势POM设计原则POM的实现 selenium的常用操作处理动态元素截图操作勾选复选框多层框架/窗口定位操作下拉框上传文件操作处理弹窗切换窗口拖拽操作 如何处理浏览器驱动更新导致的问题selenium与网站监控监听网页内容变化监控网络请求 seleni…...

宏集eX710物联网工控屏在石油开采机械中的应用与优势
案例概况 客户:天津某石油机械公司 应用产品:宏集eX710物联网工控屏 应用场景:钻井平台设备控制系统 一、应用背景 石油开采和生产过程复杂,涵盖钻井平台、采油设备、压缩机、分离器、管道输送系统等多种机械设备。这些设备通…...

linux——vi命令常用操作
一、vi模式 vi一般分为三种模式,分别是命令行模式、插入模式、末行模式 1.命令模式:控制屏幕光标的移动,按 :进入末行模式,按 i(其他插入命令也可) 进入插入模式; 2.插入模式&…...
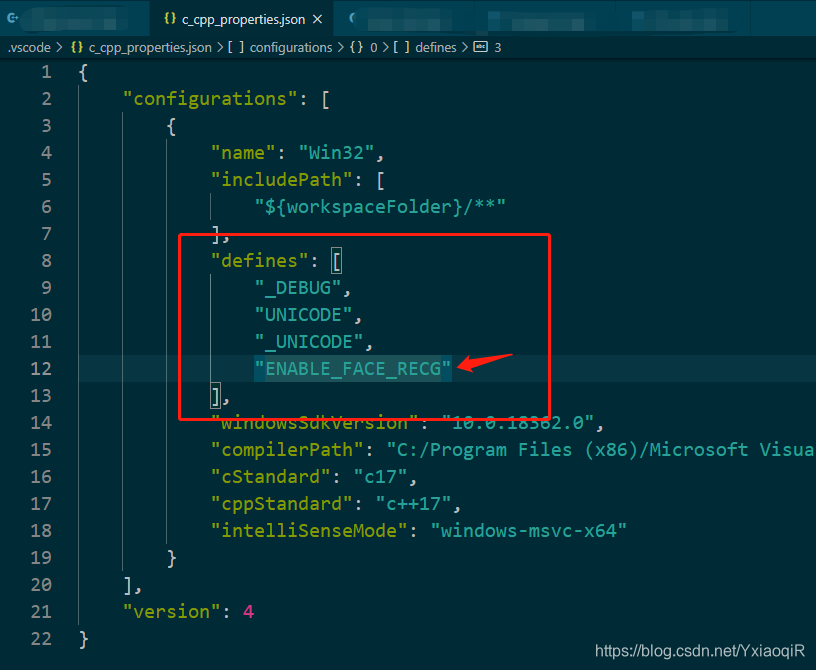
vscode添加全局宏定义
利用vscode编辑代码时,设置了禁用非活动区域着色后,在一些编译脚本中配置的宏又识别不了 遇到#ifdef包住的代码就会变暗色,想查看代码不是很方便。如下图: 一 解决: 在vscode中添加全局宏定义。 二 步骤:…...

重装荣耀X14笔记本电脑踩坑记
这几天趁着有国补搞了台荣耀 X14笔记本电脑。到手后第一件事情对我来说当然是要重装成Windows 11 LTSC版。所以按以往的经验做了个USB启动安装盘,但发现上电后按F12能进入启动设备选择,可是USB分类下没有任何设备。重启按F2进入设置界面,关闭…...

Android `android.graphics.drawable` 包深度解析:架构与设计模式
Android android.graphics.drawable 包深度解析:架构与设计模式 目录 引言Drawable 概述Drawable 的架构 Drawable 类层次结构Drawable 的核心方法Drawable 的设计模式 装饰者模式工厂模式状态模式常用 Drawable 子类解析 BitmapDrawableShapeDrawableLayerDrawableStateList…...

Kotlin语言的软件工程
Kotlin语言的软件工程 引言 在现代软件开发中,选择合适的编程语言是项目成功的关键之一。随着移动互联网的迅猛发展,以及大数据和人工智能等新兴技术的崛起,Kotlin语言凭借其简洁、高效和安全等特性,迅速崛起为备受欢迎的编程语…...
)
面试经典 150 题——数组/字符串(一)
文章目录 1、合并两个有序数组1.1 题目链接1.2 题目描述1.3 解题代码1.4 解题思路 2、移除元素2.1 题目链接2.2 题目描述2.3 解题代码2.4 解题思路 3、删除有序数组中的重复项3.1 题目链接3.2 题目描述3.3 解题代码3.4 解题思路 4、删除有序数组中的重复项 II4.1 题目链接4.2 题…...

使用亚马逊针对 PyTorch 和 MinIO 的 S3 连接器实现可迭代式数据集
2023 年 11 月,Amazon 宣布推出适用于 PyTorch 的 S3 连接器。适用于 PyTorch 的 Amazon S3 连接器提供了专为 S3 对象存储构建的 PyTorch 数据集基元(数据集和数据加载器)的实现。它支持用于随机数据访问模式的地图样式数据集和用于流式处理…...

TestMAX/DFT Compiler:时序单元的类型、连接顺序和后DFT优化
相关阅读 TestMAX/DFT Compilerhttps://blog.csdn.net/weixin_45791458/category_12865937.html?spm1001.2014.3001.5482 时序单元的状态 未映射的时序单元(Unmapped Sequential Cell) 在Design Compiler读取了一个RTL设计后,Design Compiler内置的HDL Compiler工…...

CAN201 Introduction to Networking(计算机网络)Pt.3 网络层
文章目录 4.Network Layter(网络层)4.1 Overview4.2 Router(路由器)4.3 Internet Protocol4.4 IPv4 addressing4.5 NAT(network address translation,网路地址转换)4.6 IPv64.7 Generalized For…...

App Factory:简化和加速私人应用开发
App Factory是Codigger提供的一套先进的开发工具、库和API,旨在帮助开发人员在现有的软件基础上添加特定的功能或扩展。它为私人应用的创建、开发和发布提供了一整套先进的工具集、集成的相关资源库以及强大的API接口,使开发者能够在现有的Codigger架构之…...

PHP语言laravel框架中基于Redis的异步队列使用实践与原理
在 Laravel 中,基于 Redis 的异步队列是通过 Laravel 的队列系统与 Redis 服务结合来实现的。这种队列机制允许你将任务推送到队列中,并由后台工作进程异步处理这些任务。这样,你就可以将耗时的操作(如发送邮件、处理视频、数据同…...

全面Kafka监控方案:从配置到指标
文章目录 1.1.监控配置1.2.监控工具1.3.性能指标系统相关指标GC相关指标JVM相关指标Topic相关指标Broker相关指标 1.4.性能指标说明1.5.重要指标说明 1.1.监控配置 开启JMX服务端口:kafka基本分为broker、producer、consumer三个子项,每一项的启动都需要…...

kipotix4靶机实战
信息收集 1.判断靶机ip 原理:开靶机之前nmap扫一次网段,再开靶机之后扫一次,查看多出来的ip就是靶机ip ip192.168.98.1742.判断端口服务,系统版本 a.确定端口 b.-p指定端口进一步收集 c.信息筛选 1.端口:22,80,139,…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...
