[C#] 复数乘法的跨平台SIMD硬件加速向量算法(不仅支持X86的Sse、Avx、Avx512,还支持Arm的AdvSimd)
文章目录
- 一、简单算法
- 二、向量算法
- 2.1 算法思路
- 2.1.1 复数乘法的数学定义
- 2.1.2 复数的数据布局
- 2.1.3 第1步:计算 `(a*c) + (-b*d)i`
- 2.1.4 第2步:计算 `(a*d) + (b*c)i`
- 2.1.5 第3步:计算结果合并
- 2.2 算法实现(UseVectors)
- 2.3 深入探讨
- 2.3.1 YGroup2Transpose的深入探讨
- 2.3.2 HorizontalAdd(水平加法)算法与本算法的区别
- 2.4 用引用代替指针, 摆脱unsafe关键字(UseVectorsSafeDo)
- 2.5 循环展开(UseVectorsX2Do)
- 2.6 512位算法(UseVector512sX2Do)
- 三、基准测试结果
- 3.1 X86 架构
- 3.1.1 更深入的说明
- 3.2 Arm 架构
- 附录
将复数乘法改造为SIMD向量算法,是稍微有一些的难度的。首个难点是需要重新调整元素的位置,才能满足复数乘法公式。而“调整元素的位置”与内存中数据布局有关,不同办法的性能不同。还需考虑优化内存访问等细节。
最近知乎有个 帖子 讨论了该话题,且 hez2010 给出了修正后的基于Avx指令集 HorizontalAdd(水平加法)的向量算法。
于是我来说说基于 Shuffle(换位)的向量算法吧。且这些算法是跨平台的,同一份源代码,能在 X86(Sse、Avx等指令集)及Arm(AdvSimd指令集)等架构上运行,且均享有SIMD硬件加速。本文还介绍了512位向量算法,用于对比测试Avx512指令集的硬件加速。
一、简单算法
先回顾一下 .NET 里怎么做复数乘法。
从 .NET 4.0 开始,提供了 Complex类型。于是不必手工地根据数学知识来编写复数乘法函数,而是可以使用Complex类型来做复数运算,简化了不少。
为了便于进行基准测试,可以将一个数组作为输入参数,随后对各个元素自乘并进行累加。最后返回累加的结果。
public static Complex mul(Complex[] a) {Complex c = 0;for (int i = 0; i < a.Length; i++) {c += a[i] * a[i];}return c;
}
二、向量算法
2.1 算法思路
2.1.1 复数乘法的数学定义
向量类型并未提供复数乘法的方法,于是需要手工地根据数学知识来编写复数乘法函数了。
先来回顾一下复数乘法的数学定义。
(a + bi)*(c + di) = (ac – bd) + (ad + bc)i

a + bi 是乘法的左侧参数, c + di 是乘法的右侧参数。
数学表达式一般喜欢省略“乘法运算符”。例如上式里,“ac”其实表示“a*c”。为了能使乘法运算更清晰,上式可以写成下面的形式。
(a + bi)*(c + di) = (a*c – b*d) + (a*d + b*c)i
可以看出,复数乘法是由4次实数乘法,以及若干个加减运算所组成。
2.1.2 复数的数据布局
Complex 是一个结构体,其中顺序存放了2个Double类型的成员,分别为“实部”与“虚部”。Double类型是64位的,2个Double就是128位,于是 Complex类型是128位的,即16字节。
由于大多数架构都支持128位向量的SIMD硬件加速。所以 C# 程序在使用Complex类型时,其实已经享受到SIMD硬件加速了。这就是为什么手写的向量算法,有时还比不过 Complex的原因。于是需要更仔细的进行优化。
对于 Complex数组,数据是连续存放的。于是使用向量类型从Complex数组加载数据时,能加载到整数个Complex。
- 对于128位向量,能存放1个Complex。以Double元素的视角来看,向量中的元素依次是
[a, b]。注:“a”代表复数的“实部”,“b”代表复数的“虚部”。 - 对于256位向量,能存放2个Complex。以Double元素的视角来看,向量中的元素依次是
[a0, b0, a1, b1]。 - 对于512位向量,能存放4个Complex。以Double元素的视角来看,向量中的元素依次是
[a0, b0, a1, b1, a2, b2, a3, b3]。
由于数据都是这样连续存放的,对于上面这种数据布局,本文将它简称为 a + bi 形式。后面将会经常使用这种简称。
例如将实部与虚部交换,变为 b + ai 形式。那么代表的是下面这样的数据布局。
- 128位向量:
[b, a]。 - 256位向量:
[b0, a0, b1, a1]。 - 512位向量:
[b0, a0, b1, a1, b2, a2, b3, a3]。
2.1.3 第1步:计算 (a*c) + (-b*d)i
先来观察一下 向量乘法(Vector.Multiply)对复数数据的运算效果。
假设已经将复数数据分别加载到向量a(a + bi)、向量c(c + di)之中,随后对这2个向量进行向量乘法运算。由于向量乘法依然是对逐个地对相同位置的元素做乘法处理,所以计算结果为 (a*c) + (b*d)i。可以观察到,它正好包含了“复数乘法内部的4个实数乘法”中的2项——a*c、b*d。
表示这个思路是正确的。但是可以注意到,复数乘法需要使用 -b*d,而上面的 b*d是不带“负号”的。于是我们需要对数据进行进一步的处理,将奇数位置(虚部)的元素做一次“求负”处理。Vector类型里没有单独提供这种处理的方法,于是需要自行编写算法。
对于“求负”处理,性能最高的办法是直接翻转浮点类型的符号位。在IEEE754浮点数标准里,规定了最高位是符号位,该位为0时表示正数,为1时表示负数。于是IEEE754浮点数标准里还能表达 -0.0(负零),它的最高位符号位为1,剩余数据位(阶码s、尾数m)均为0。
二进制的Xor(异或运算)可以使相关二进制进行翻转。于是,将某个浮点数,与 -0.0(负零)执行Xor运算,就能将符号位翻转,这正好是“求负”运算。
由于仅需对奇数位置求负,于是我们可以预先准备一个向量mask,它的偶数位置为 0(正零),奇数位置为 -0.0(负零)。向量c(c + di)与mask进行Xor运算后,结果是 c + (-d)i。随后再与向量a(a + bi)执行乘法,结果是 (a*c) + (-b*d)i。满足所需。
Vector<double> mask = Vectors.CreateRotate(0.0, -0.0);Vector<double> a = *p; // a + bi
var c = a; // c + di
var e = Vector.Multiply(a, Vector.Xor(c, mask)); // (a*c) + (-b*d)i
由于 Vector 的长度不是固定的,手工给mask赋值不太方便。于是这里使用 VectorTraits 库的 Vectors.CreateRotate 方法来简化赋值,它会循环将各个参数依次放置在向量的各个元素里。从而满足了“偶数为正零,奇数为负零”的要求。
Vector<double> a = *p 表示根据指针p,将数据加载到向量a。由于是复数数据,于是a的数学意义为 a + bi,即复数乘法的左侧参数。
为了与前面的“简单算法”保持一致,于是将a复制给了c。此时c的数学意义为 c + di,即复数乘法的右侧参数。
随后根据上面的经验,算出 (a*c) + (-b*d)i,赋值给向量e。
2.1.4 第2步:计算 (a*d) + (b*c)i
根据上一节的经验,使用2个步骤就能计算出 (a*d) + (b*c)i——
- 将c的实部与虚部交换,得到
(d) + (c)i,赋值给向量f。 - 对 a、f 执行向量乘法(
Vector.Multiply),便能得到(a*d) + (b*c)i。
第2步容易实现,但第1步遇到了困难——.NET 的向量方法里,没有合适的方法来做这一工作。
从.NET 7.0开始,Vector128等向量类型增加了 Shuffle 方法。用该方法,可以给向量内的元素进行换位。但是直至 .NET 8.0,Shuffle都没有硬件加速,而是使用了标量回退代码。
为了解决 Shuffle 方法没有硬件加速的问题,我开发了VectorTraits 库。它使用了各个架构的shuffle类别的指令,从而使 Shuffle 方法具有硬件加速。具体来说,它分别使用了以下指令。
- X86: 使用
_mm_shuffle_epi8等指令. - Arm: 使用
vqvtbl1q_u8指令. - Wasm: 使用
i8x16.swizzle指令.
VectorTraits 不仅为固定大小的向量类型(如 Vector128)提供了Shuffle方法,它还为自动大小的向量类型(Vector)也提供了Shuffle方法。
虽然VectorTraits的Shuffle方法是有硬件加速的,但它不是最佳办法。VectorTraits还提供了YShuffleG2方法,专门用来处理2元素组的换位。它用起来更简单,且大多数时候的性能更高。
YShuffleG2方法通过ShuffleControlG2参数来控制换位模式,例如 ShuffleControlG2.YX 表示将“XY”顺序给换成“YX”顺序,即我们所需的“实部与虚部交换”。
根据这些信息,便能完成第2步的代码了。
var f = Vectors.YShuffleG2(c, ShuffleControlG2.YX); // (d) + (c)i
f = Vector.Multiply(a, f); // (a*d) + (b*c)i
2.1.5 第3步:计算结果合并
经过上面的步骤,已经算出了 (a*c) + (-b*d)i、(a*d) + (b*c)i。复数乘法规则是 (a*c – b*d) + (a*d + b*c)i,实数乘法的步骤均处理完了,还剩下加法与数据变换的处理。
向量加法与向量乘法一样,是对逐个地对相同位置的元素做相加处理。于是我们需要将上面的那2组数据,变换为 (a*c) + (a*d)i、(-b*d) + (b*c)i,这样才好交给向量加法去处理。
可以观察到,这种变换,就是 2x2矩阵的转置操作。将数据写成矩阵形式,便能清晰看出它是转置操作。
[(a*c) (-b*d)] --> [(a*c) (a*d)]
[(a*d) (b*c)] --> [(-b*d) (b*c)]
VectorTraits库提供了YGroup2Transpose方法,用它便能实现2x2矩阵的转置操作。
var g = Vectors.YGroup2Transpose(e, f, out var h); // g is {(a*c) + (a*d)i}; h is {(-b*d) + (b*c)i}
g += h; // (a*c - b*d) + (a*d + b*c)i
自此,完成了复数乘法的计算。
2.2 算法实现(UseVectors)
有了上面的思路,便能编写出对数组计算向量乘法累加的算法了。源代码如下。
public static unsafe Complex UseVectorsDo(Complex[] numbers) {int blockWidth = Vector<double>.Count / 2; // Complex is double*2int cntBlock = numbers.Length / blockWidth;int cntRem = numbers.Length - (cntBlock * blockWidth);// -- Processs body.Complex result;Vector<double> acc = Vector<double>.Zero;Vector<double> mask = Vectors.CreateRotate(0.0, -0.0);fixed (Complex* pnumbers = numbers) {Vector<double>* p = (Vector<double>*)pnumbers; // Set pointer to numbers[0].Vector<double>* pEnd = p + cntBlock;while (p < pEnd) {// -- Complex multiply: (a + bi)*(c + di) = (ac – bd) + (ad + bc)iVector<double> a = *p; // a + bivar c = a; // c + divar e = Vector.Multiply(a, Vector.Xor(c, mask)); // (a*c) + (-b*d)ivar f = Vectors.YShuffleG2(c, ShuffleControlG2.YX); // (d) + (c)if = Vector.Multiply(a, f); // (a*d) + (b*c)ivar g = Vectors.YGroup2Transpose(e, f, out var h); // g is {(a*c) + (a*d)i}; h is {(-b*d) + (b*c)i}g += h; // (a*c - b*d) + (a*d + b*c)i// Sumacc += g;// Next++p;}// Vector to a Complex.double re = 0.0, im = 0.0;for (int i = 0; i < Vector<double>.Count; i += 2) {re += acc[i];im += acc[i + 1];}result = new Complex(re, im);// -- Processs remainder.Complex* q = (Complex*)pEnd;for (int i = 0; i < cntRem; i++) {result += (*q) * (*q);// Next++q;}}return result;
}
该方法是用指针来处理数据的。代码分为4个部分。
- 最前面的部分,是变量初始化。例如计算 cntBlock(有多少个块)、cntRem(剩余部分有多少个复数)等。
- “Processs body”是向量处理的主体代码,它构造好mask,并计算好指针地址,随后循环处理主要数据(向量类型的整数倍的数据)。用的就是上面提到的算法。
- “Vector to a Complex”是将向量里存放的复数数据,转换为单个复数。
- “Processs remainder”是剩余部分的处理。
2.3 深入探讨
2.3.1 YGroup2Transpose的深入探讨
此时,有些读者可能会产生疑问——Vector类型有可能是256位(CPU支持Avx2指令集时),这时向量里不只是2个Double,而是4个Double,YGroup2Transpose还能正常工作吗?
答案是——YGroup2Transpose当然能正常工作。
当 Vector 为256位时,4个Double被分为了2组。既可以看作有2组2x2矩阵,随后分别进行了矩阵转置处理。正好Complex类型是128位的,由2个Double所组成,与2x2矩阵相匹配。
从中可以看出规律——假设向量里可以存放 N*2 个元素(如Double元素),那么 YGroup2Transpose可以对 N组2x2矩阵进行转置。且“N个Complex”做复数乘法时,能使用YGroup2Transpose方法。
对于X86架构,YGroup2Transpose是用Shuffle类别的指令来实现的。对于Arm架构,它是使用 AdvSimd中转置类指令 TRN1、TRN2 来实现的,效率很高。
另注:为了使方法名的可读性更高,未来计划将 YGroup2Transpose 改名为 YMatrix2Transpose。初步计划将在VectorTraits库下一个大版本,做这个改名。
2.3.2 HorizontalAdd(水平加法)算法与本算法的区别
HorizontalAdd(水平加法)算法与本算法是非常相似的,仅“第3步:计算结果合并”不同。
先来看看128位向量时的运算情况。HorizontalAdd 会将 相邻2个元素相加,并把结果放在1个元素里,于是2个向量在处理后被合并成了1个向量。
经过前面2步,已经算出了 (a*c) + (-b*d)i、(a*d) + (b*c)i。此时进行 HorizontalAdd,便会算出 (a*c – b*d) + (a*d + b*c)i,正好是复数乘法的运算结果!
随后改为用Avx指令集的256位向量来实现,虽然也能正确算出结果,但其实此时 HorizontalAdd 是Avx指令集的特殊版本——它不是对整个向量进行水平加法的,而是按每128位小道(lane)来做水平加法的。
例如Double类型的源数据是 [x0, x1, x2, x3]、[y0, y1, y2, y3],那么这2种水平加法的结果是不同的——
- 整256位向量:
[x0+x1, x2+x3, y0+y1, y2+y3] - 每128位小道:
[x0+x1, y0+y1, x2+x3, y2+y3]
第1种方式(整256位向量)比较符合常规思路,但第2种方式( 每128位小道)在很多时候更有用。例如复数类型Complex是128位,要使Complex的运算结果正确,于是需要第2种方式( 每128位小道)的水平加法。幸好Avx指令集,提供的就是第2种方式的水平加法,从而方便了计算。
虽然仅需要1条水平加法指令就能实现“第3步:计算结果合并”,但由于该指令牵涉2个向量的水平操作,所以处理器会稍微多花一些时间。下面摘录了Intel手册对水平加法指令(vhaddpd)的说明,“Latency and Throughput”就是介绍延迟与吞吐率的,可以发现它的值比较高。
__m256d _mm256_hadd_pd (__m256d a, __m256d b)
#include <immintrin.h>
Instruction: vhaddpd ymm, ymm, ymm
CPUID Flags: AVX
Description
Horizontally add adjacent pairs of double-precision (64-bit) floating-point elements in a and b, and pack the results in dst.
Operation
dst[63:0] := a[127:64] + a[63:0]
dst[127:64] := b[127:64] + b[63:0]
dst[191:128] := a[255:192] + a[191:128]
dst[255:192] := b[255:192] + b[191:128]
dst[MAX:256] := 0Latency and Throughput
Architecture Latency Throughput (CPI)
Alderlake 5 2
Icelake Intel Core 6 2
Icelake Xeon 6 2
Sapphire Rapids 5 2
Skylake 7 2
对于现代处理器,水平加法算法与本算法的性能,一般是是差不多的。详见“三、基准测试结果”。
而且Avx512系列指令集里,尚未提供512位的水平加法指令,故更推荐使用本算法来处理复数加法。
2.4 用引用代替指针, 摆脱unsafe关键字(UseVectorsSafeDo)
从 C# 7.3开始,可以用引用代替指针, 摆脱unsafe关键字与fixed语句。其实编程思路与指针差不多的,只是一些地方需要换一种写法。具体办法可参考《C# 使用SIMD向量类型加速浮点数组求和运算(4):用引用代替指针, 摆脱unsafe关键字,兼谈Unsafe类的使用》。
改造后的代码如下。
public static Complex UseVectorsSafeDo(Complex[] numbers) {int blockWidth = Vector<double>.Count / 2; // Complex is double*2int cntBlock = numbers.Length / blockWidth;int cntRem = numbers.Length - (cntBlock * blockWidth);// -- Processs body.Vector<double> acc = Vector<double>.Zero;Vector<double> mask = Vectors.CreateRotate(0.0, -0.0);ref Vector<double> p = ref Unsafe.As<Complex, Vector<double>>(ref numbers[0]); // Set pointer to numbers[0].ref Vector<double> pEnd = ref Unsafe.Add(ref p, cntBlock);while (Unsafe.IsAddressLessThan(ref p, ref pEnd)) {// -- Complex multiply: (a + bi)*(c + di) = (ac – bd) + (ad + bc)iVector<double> a = p; // a + bivar c = a; // c + divar e = Vector.Multiply(a, Vector.Xor(c, mask)); // (a*c) + (-b*d)ivar f = Vectors.YShuffleG2(c, ShuffleControlG2.YX); // (d) + (c)if = Vector.Multiply(a, f); // (a*d) + (b*c)ivar g = Vectors.YGroup2Transpose(e, f, out var h); // g is {(a*c) + (a*d)i}; h is {(-b*d) + (b*c)i}g += h; // (a*c - b*d) + (a*d + b*c)i// Sumacc += g;// Nextp = ref Unsafe.Add(ref p, 1);}// Vector to a Complex.double re = 0.0, im = 0.0;for (int i = 0; i < Vector<double>.Count; i += 2) {re += acc[i];im += acc[i + 1];}Complex result = new Complex(re, im);// -- Processs remainder.ref Complex q = ref Unsafe.As<Vector<double>, Complex>(ref pEnd);for (int i = 0; i < cntRem; i++) {result += q * q;// Nextq = ref Unsafe.Add(ref q, 1);}return result;
}
上面的代码,与指针版代码(UseVectorsDo)是等价的。程序的性能,也是差不多的。
2.5 循环展开(UseVectorsX2Do)
对于小循环,循环时的跳转处理也是一笔不小的开销。此时可以使用循环展开的办法,在循环内处理多条数据,从而使循环开销的占比减低。优化了性能。
这里选用了2倍循环展开。它还能带来一个好处,就是能将2元素组换位(YShuffleG2),改为4元素组换位(YShuffleG4X2)。因为一些架构上有“4元素组换位”的专业指令(例如 Avx2.Permute4x64),性能很高。
当初因为自动大小向量有时只有128位,只能存放2个Double,无法满足“4元素组换位”的要求,故谨慎的使用了YShuffleG2方法。而现在有了2倍数据,即使自动大小向量只有128位,也能保证至少共有4个元素,故可以使用 YShuffleG4X2方法。
YShuffleG4X2方法通过ShuffleControlG4参数来控制换位模式,例如 ShuffleControlG4.YXWZ 表示将“XYZW”顺序给换成“YXWZ”顺序,即我们所需的“实部与虚部交换”。(其实, ShuffleControlG4.YXWZ 就是 Avx2.Permute4x64 指令的参数 0b10110001,现在用枚举来描述,代码的可读性更好)
由于现在所用的ShuffleControlG4参数是固定的常数,于是还可以使用 YShuffleG4X2_Const,它的性能一般更好。
根据上面的经验,便能编写出2倍循环展开时的算法了。源代码如下。
public static Complex UseVectorsX2Do(Complex[] numbers) {const int batchWidth = 2; // X2int blockWidth = Vector<double>.Count * batchWidth / 2; // Complex is double*2int cntBlock = numbers.Length / blockWidth;int cntRem = numbers.Length - (cntBlock * blockWidth);// -- Processs body.Vector<double> acc = Vector<double>.Zero;Vector<double> acc1 = Vector<double>.Zero;Vector<double> mask = Vectors.CreateRotate(0.0, -0.0);ref Vector<double> p = ref Unsafe.As<Complex, Vector<double>>(ref numbers[0]); // Set pointer to numbers[0].ref Vector<double> pEnd = ref Unsafe.Add(ref p, cntBlock * batchWidth);while (Unsafe.IsAddressLessThan(ref p, ref pEnd)) {// -- Complex multiply: (a + bi)*(c + di) = (ac – bd) + (ad + bc)iVector<double> a0 = p; // a + bivar a1 = Unsafe.Add(ref p, 1);var c0 = a0; // c + divar c1 = a1;var e0 = Vector.Multiply(a0, Vector.Xor(c0, mask)); // (a*c) + (-b*d)ivar e1 = Vector.Multiply(a1, Vector.Xor(c1, mask));var f0 = Vectors.YShuffleG4X2_Const(c0, c1, ShuffleControlG4.YXWZ, out var f1); // (d) + (c)if0 = Vector.Multiply(a0, f0); // (a*d) + (b*c)if1 = Vector.Multiply(a1, f1);var g0 = Vectors.YGroup2Transpose(e0, f0, out var h0); // g is {(a*c) + (a*d)i}; h is {(-b*d) + (b*c)i}var g1 = Vectors.YGroup2Transpose(e1, f1, out var h1);g0 += h0; // (a*c - b*d) + (a*d + b*c)ig1 += h1;// Sumacc += g0;acc1 += g1;// Nextp = ref Unsafe.Add(ref p, batchWidth);}acc += acc1;// Vector to a Complex.double re = 0.0, im = 0.0;for (int i = 0; i < Vector<double>.Count; i += 2) {re += acc[i];im += acc[i + 1];}Complex result = new Complex(re, im);// -- Processs remainder.ref Complex q = ref Unsafe.As<Vector<double>, Complex>(ref pEnd);for (int i = 0; i < cntRem; i++) {result += q * q;// Nextq = ref Unsafe.Add(ref q, 1);}return result;
}
2.6 512位算法(UseVector512sX2Do)
.NET 8.0 新增了对 X86架构的Avx512系列指令集的支持,且新增了 Vector512类型。
VectorTraits 3.0版已经支持了Avx512系列指令集,于是能够很容易将自动大小向量的算法,改造为512位向量的算法。只需要做文本替换,将“Vector”替换为“Vector512”,便基本完成了改造,顶多有少量报错需修正。而不用学习复杂的Avx512指令集,大大降低了门槛。源代码如下。
#if NET8_0_OR_GREATER[Benchmark]
public void UseVector512sX2() {if (!Vector512s.IsHardwareAccelerated) throw new NotSupportedException("Vector512 does not have hardware acceleration!");_destination = UseVector512sX2Do(_array);
}public static Complex UseVector512sX2Do(Complex[] numbers) {const int batchWidth = 2; // X2int blockWidth = Vector512<double>.Count * batchWidth / 2; // Complex is double*2int cntBlock = numbers.Length / blockWidth;int cntRem = numbers.Length - (cntBlock * blockWidth);// -- Processs body.Vector512<double> acc = Vector512<double>.Zero;Vector512<double> acc1 = Vector512<double>.Zero;Vector512<double> mask = Vector512s.CreateRotate(0.0, -0.0);ref Vector512<double> p = ref Unsafe.As<Complex, Vector512<double>>(ref numbers[0]); // Set pointer to numbers[0].ref Vector512<double> pEnd = ref Unsafe.Add(ref p, cntBlock * batchWidth);while (Unsafe.IsAddressLessThan(ref p, ref pEnd)) {// -- Complex multiply: (a + bi)*(c + di) = (ac – bd) + (ad + bc)iVector512<double> a0 = p; // a + bivar a1 = Unsafe.Add(ref p, 1);var c0 = a0; // c + divar c1 = a1;var e0 = Vector512s.Multiply(a0, Vector512s.Xor(c0, mask)); // (a*c) + (-b*d)ivar e1 = Vector512s.Multiply(a1, Vector512s.Xor(c1, mask));var f0 = Vector512s.YShuffleG4X2_Const(c0, c1, ShuffleControlG4.YXWZ, out var f1); // (d) + (c)if0 = Vector512s.Multiply(a0, f0); // (a*d) + (b*c)if1 = Vector512s.Multiply(a1, f1);var g0 = Vector512s.YGroup2Transpose(e0, f0, out var h0); // g is {(a*c) + (a*d)i}; h is {(-b*d) + (b*c)i}var g1 = Vector512s.YGroup2Transpose(e1, f1, out var h1);g0 += h0; // (a*c - b*d) + (a*d + b*c)ig1 += h1;// Sumacc += g0;acc1 += g1;// Nextp = ref Unsafe.Add(ref p, batchWidth);}acc += acc1;// Vector to a Complex.double re = 0.0, im = 0.0;for (int i = 0; i < Vector512<double>.Count; i += 2) {re += acc[i];im += acc[i + 1];}Complex result = new Complex(re, im);// -- Processs remainder.ref Complex q = ref Unsafe.As<Vector512<double>, Complex>(ref pEnd);for (int i = 0; i < cntRem; i++) {result += q * q;// Nextq = ref Unsafe.Add(ref q, 1);}return result;
}#endif // NET8_0_OR_GREATER
注意,从.NET 8.0才开始支持 Vector512,故需要使用条件编译符号NET8_0_OR_GREATER进行判断。
由于现在有不少处理器尚未支持 Avx512系列指令集,于是需要用if语句判断一下“Vector512s.IsHardwareAccelerated”是否为真。否则就不要执行了。
三、基准测试结果
3.1 X86 架构
X86架构下的基准测试结果如下。
BenchmarkDotNet v0.14.0, Windows 11 (10.0.26100.2605)
AMD Ryzen 7 7840H w/ Radeon 780M Graphics, 1 CPU, 16 logical and 8 physical cores
.NET SDK 9.0.101[Host] : .NET 8.0.11 (8.0.1124.51707), X64 RyuJIT AVX-512F+CD+BW+DQ+VL+VBMIDefaultJob : .NET 8.0.11 (8.0.1124.51707), X64 RyuJIT AVX-512F+CD+BW+DQ+VL+VBMI| Method | Count | Mean | Error | StdDev | Ratio | Code Size |
|----------------- |------ |---------:|---------:|---------:|------:|----------:|
| CallMul | 65536 | 44.45 us | 0.329 us | 0.308 us | 1.00 | 128 B |
| CallMul2 | 65536 | 92.50 us | 0.104 us | 0.087 us | 2.08 | NA |
| UseVectors | 65536 | 22.48 us | 0.068 us | 0.061 us | 0.51 | NA |
| UseVectorsSafe | 65536 | 22.47 us | 0.084 us | 0.070 us | 0.51 | NA |
| UseVectorsX2 | 65536 | 17.95 us | 0.080 us | 0.075 us | 0.40 | NA |
| UseVector512sX2 | 65536 | 17.26 us | 0.179 us | 0.167 us | 0.39 | NA |
| Hez2010Simd_Mul2 | 65536 | 23.69 us | 0.206 us | 0.193 us | 0.53 | NA |
| Hez2010Simd | 65536 | 23.01 us | 0.151 us | 0.134 us | 0.52 | 298 B |
方法说明——
- CallMul: 简单算法。
- CallMul2: 知乎帖子提出给出的有问题的Avx向量算法。
- UseVectors: 指针写法的向量算法(2.2 算法实现)。
- UseVectorsSafe: 引用写法的安全向量算法(2.4 用引用代替指针, 摆脱unsafe关键字)。
- UseVectorsX2: 2倍循环展开的向量算法(2.5 循环展开)。
- UseVector512sX2: 2倍循环展开的512位向量算法(2.6 512位算法)。
- Hez2010Simd_Mul2: hez2010将CallMul2修正后的向量算法。
- Hez2010Simd: hez2010的安全向量算法。
现在来对比一下各个方法的性能。
- CallMul2: 44.45/92.50 ≈ 0.4805(倍)。
- UseVectors: 44.45/22.48 ≈ 1.9773(倍)。
- UseVectorsSafe: 44.45/22.47 ≈ 1.9782(倍)。
- UseVectorsX2: 44.45/17.95 ≈ 2.4763(倍)。性能是UseVectorsSafe的 22.47/17.95 ≈ 1.2518(倍)
- UseVector512sX2: 44.45/17.26 ≈ 2.5753(倍)。性能是UseVectorsSafe的 22.47/17.26 ≈ 1.3019(倍)
- Hez2010Simd_Mul2: 44.45/23.69 ≈ 1.8763(倍)。
- Hez2010Simd: 44.45/23.01 ≈ 1.9318(倍)。
首先可以注意到,UseVectors、UseVectorsSafe的性能几乎是一样的。这是因为不论是指针写法,还是引用写法,它们的算法是相同的,所以性能是一样的。而且若观察JIT生成汇编代码,你会发现它们基本是一样的。
其次,可以发现 Hez2010Simd_Mul2、Hez2010Simd、UseVectors、UseVectorsSafe 这4种方法的耗时很接近,都是23us左右。差距很小,可看作测试误差范围内。故可以得出结论,水平加法算法与本算法的性能是几乎是一样的。Avx是256位向量宽度,比Sse的128位向量宽度翻了一倍,理论性能是2倍。现在的测试结果,很接近这个理论值。
再来看 UseVectorsX2,会发现它的性能又有提升,比起普通向量算法(UseVectorsSafe)快了20%左右。看来此时做循环展开,确实有效。
最后来看 UseVector512sX2。Avx512是512位向量宽度,是Sse的128位向量宽度的4倍,理论性能应该是4倍。但是实际测试时,它仅比 UseVectorsX2 稍微快了一点点。
这是因为当前处理器是 Zen4微架构的,它并没有专门的512位运算单元,而是通过2个256位运算单元组合而成的,还不能完全发挥Avx512指令集的潜力。若换成 Zen5、Sapphire Rapids等具有专门512位运算单元的微架构的处理器,能获得进一步性能提升。
3.1.1 更深入的说明
仔细观察一下上面的测试结果,会发现本算法(UseVectorsSafe)比起水平加法算法(Hez2010Simd),稍微快一点点。
其实这跟CPU微架构有关。在AMD的处理器上,很多时候是本算法稍微快一点;而在Intel的处理器上,很多时候是水平加法算法稍微快一点。
而且在 Intel 处理器上测试 UseVectorsX2 算法时,有时它的性能与 UseVectorsSafe 相差不大。这也是CPU微架构的差别。
3.2 Arm 架构
同样的源代码可以在 Arm 架构上运行。基准测试结果如下。
BenchmarkDotNet v0.14.0, macOS Sequoia 15.1.1 (24B91) [Darwin 24.1.0]
Apple M2, 1 CPU, 8 logical and 8 physical cores
.NET SDK 8.0.204[Host] : .NET 8.0.4 (8.0.424.16909), Arm64 RyuJIT AdvSIMDDefaultJob : .NET 8.0.4 (8.0.424.16909), Arm64 RyuJIT AdvSIMD| Method | Count | Mean | Error | StdDev | Ratio | RatioSD |
|----------------- |------ |---------:|---------:|---------:|------:|--------:|
| CallMul | 65536 | 56.30 us | 0.051 us | 0.045 us | 1.00 | 0.00 |
| CallMul2 | 65536 | NA | NA | NA | ? | ? |
| UseVectors | 65536 | 56.90 us | 0.468 us | 0.415 us | 1.01 | 0.01 |
| UseVectorsSafe | 65536 | 56.32 us | 0.019 us | 0.017 us | 1.00 | 0.00 |
| UseVectorsX2 | 65536 | 47.18 us | 0.025 us | 0.024 us | 0.84 | 0.00 |
| UseVector512sX2 | 65536 | NA | NA | NA | ? | ? |
| Hez2010Simd_Mul2 | 65536 | NA | NA | NA | ? | ? |
| Hez2010Simd | 65536 | NA | NA | NA | ? | ? |
首先可以注意到,CallMul2、Hez2010Simd_Mul2、Hez2010Simd 都无法执行基准测试。这是因为它们都依赖Avx指令集,但现在是Arm架构的处理器,没有Avx指令集,于是报错了。
此时便能体现出本文介绍的算法的优势了——支持跨平台。同一份源代码,能在 X86(Sse、Avx等指令集)及Arm(AdvSimd指令集)等架构上运行,且均享有SIMD硬件加速。
UseVector512sX2是我们主动抛出了异常。虽然同一份源代码可以运行,但由于此时没有硬件加速,测试起来没有意义。故不必测试。
随后来对比一下各个方法的性能。
- UseVectors: 56.30/56.90 ≈ 0.9895(倍)。
- UseVectorsSafe: 56.30/56.32 ≈ 0.9996(倍)。
- UseVectorsX2: 56.30/47.18 ≈ 1.1933(倍)。
UseVectors、UseVectorsSafe的耗时,与CallMul的结果几乎相同。前面提到过,Complex类型内部是已经使用了128位向量加速的。由于Arm架构的AdvSimd指令集是 128位的,于是此时 Vector类型的宽度也是128位的。所以此时用Vector类型实现的算法,理论上跟Complex类型的性能是一样的。
而UseVectorsX2比CallMul快20%左右。这表示此时做循环展开,确实有效。
附录
- 完整源代码: https://github.com/zyl910/VectorTraits.Sample.Benchmarks/blob/main/VectorTraits.Sample.Benchmarks.Inc/Complexes/ComplexMultiplySumBenchmark.cs
- YGroup2Transpose 的文档: https://zyl910.github.io/VectorTraits_doc/api/Zyl.VectorTraits.Vectors.YGroup2Transpose.html
- YShuffleG2 的文档: https://zyl910.github.io/VectorTraits_doc/api/Zyl.VectorTraits.Vectors.YShuffleG2.html
YShuffleG4X2_Const的文档: https://zyl910.github.io/VectorTraits_doc/api/Zyl.VectorTraits.Vectors.YShuffleG4X2_Const.html- VectorTraits 的NuGet包: https://www.nuget.org/packages/VectorTraits
- VectorTraits 的在线文档: https://zyl910.github.io/VectorTraits_doc/
- VectorTraits 源代码: https://github.com/zyl910/VectorTraits
- C#simd使用Avx类的代码比普通的for循环代码慢,什么原因呢? - hez2010的回答 - 知乎
- C# 使用SIMD向量类型加速浮点数组求和运算(4):用引用代替指针, 摆脱unsafe关键字,兼谈Unsafe类的使用
- 《[C#] 24位图像水平翻转的跨平台SIMD硬件加速向量算法的关键——YShuffleX3Kernel源码解读(如Avx2解决shuffle的跨lane问题、Avx512优化等)》
相关文章:

[C#] 复数乘法的跨平台SIMD硬件加速向量算法(不仅支持X86的Sse、Avx、Avx512,还支持Arm的AdvSimd)
文章目录 一、简单算法二、向量算法2.1 算法思路2.1.1 复数乘法的数学定义2.1.2 复数的数据布局2.1.3 第1步:计算 (a*c) (-b*d)i2.1.4 第2步:计算 (a*d) (b*c)i2.1.5 第3步:计算结果合并 2.2 算法实现(UseVectors)2.…...

C#WPF基础介绍/第一个WPF程序
什么是WPF WPF(Windows Presentation Foundation)是微软公司推出的一种用于创建窗口应用程序的界面框架。它是.NET Framework的一部分,提供了一套先进的用户界面设计工具和功能,可以实现丰富的图形、动画和多媒体效果。 WPF 使用…...
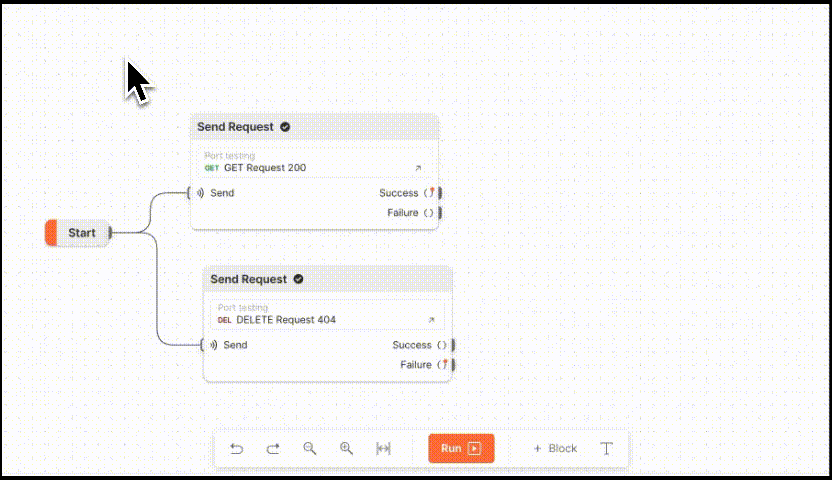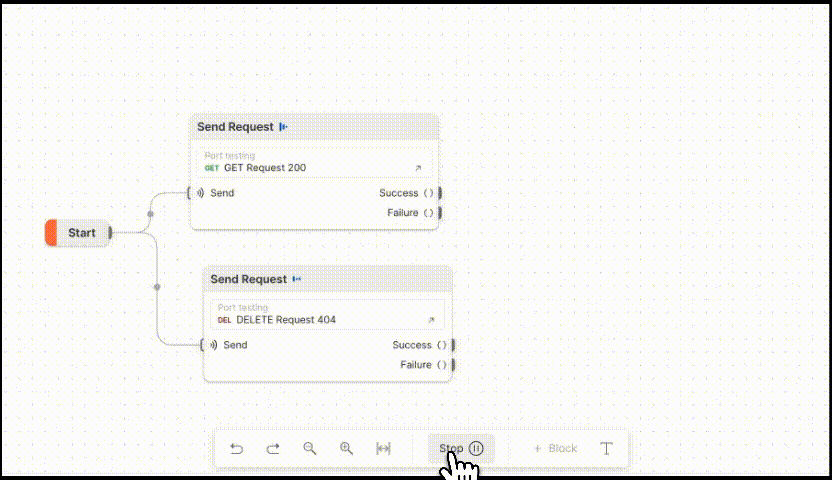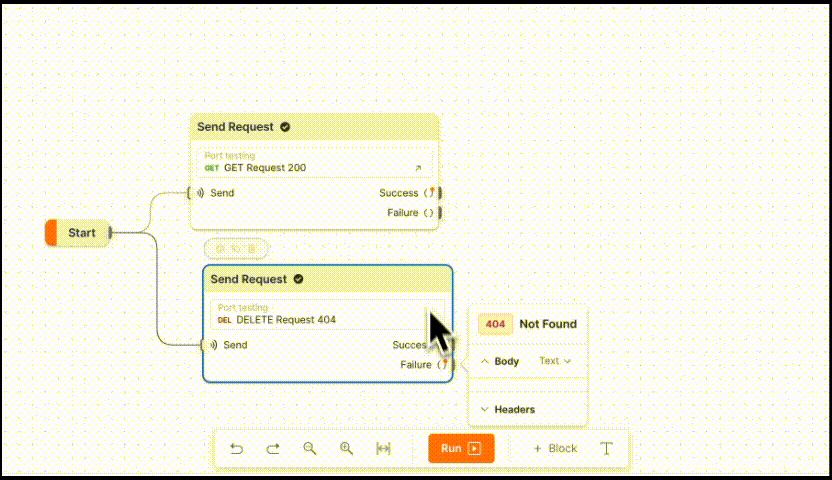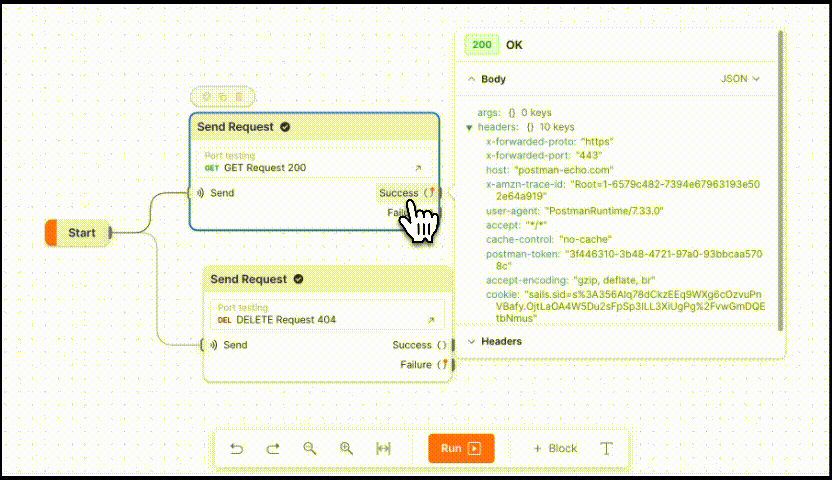
强大的接口测试可视化工具:Postman Flows
Postman Flows是一种接口测试可视化工具,可以使用流的形式在Postman工作台将请求接口、数据处理和创建实际流程整合到一起。如下图所示 Postman Flows是以API为中心的可视化应用程序开发界面。它提供了一个无限的画布用于编排和串连API,数据可视化来显示…...

系统设计及解决方案
发送验证码 1:根据手机号从Redis中获取value(验证码_时间戳) 2:如果value不为空,并且时间戳与当前时间戳的间隔小于60秒,则返回一个错误信息 3:生成随机验证码 4:调用阿里云短信服务API给用户发送短信验证码…...

从0入门自主空中机器人-2-2【无人机硬件选型-PX4篇】
1. 常用资料以及官方网站 无人机飞控PX4用户使用手册(无人机基本设置、地面站使用教程、软硬件搭建等):https://docs.px4.io/main/en/ PX4固件开源地址:https://github.com/PX4/PX4-Autopilot 飞控硬件、数传模块、GPS、分电板等…...

Linux之ARM(MX6U)裸机篇----2.汇编LED驱动实验
一,alpha的LED灯硬件原理分析 STM32 IO初始化流程 ①,使能GPIO时钟 ②,设置IO复用,复用为GPIO ③,配置GPIO的电气属性推挽,上拉下拉 ④,使用GPIO,输出高/低电平 MX6ULL IO初始化…...

e3 1220lv3 cpu-z分数
e3 1220lv3 双核四线程,1.1G频率,最低可在800MHZ运行,TDP 13W。 使用PE启动后测试cpu-z分数。 现在e3 1220lv3的价格落到69元。...

HTML5适配手机
要使 HTML5 网站适配手机设备,您可以遵循以下几个步骤和最佳实践: 1. 使用视口(Viewport) 在 HTML 文档的 <head> 部分添加视口元标签,以确保页面在移动设备上正确缩放和显示: <meta name"…...

C# 中使用 MassTransit
在生产环境中使用 MassTransit 时,通常需要进行详细的配置,包括设置连接字符串、配置队列、配置消费者、处理重试和错误队列等。以下是一个完整的示例,展示了如何在 ASP.NET Core 应用程序中配置 MassTransit,包括请求/响应模式和…...

网络编程 实现联网 b+Tree
网络编程是客户端和服务器之间通信的基础,也是现代应用开发中不可或缺的技能。在 Unity 中实现网络功能,需要结合计算机网络原理、数据结构与算法,以及网络协议的实际应用。以下是对这一块内容的详细介绍,包括每个涉及到的知识点&…...

zentao ubuntu上安装
#下载ZenTaoPMS-21.2-zbox_amd64.tar.gz(https://www.zentao.net/downloads.html) https://dl.zentao.net/zentao/21.2/ZenTaoPMS-21.2-zbox_amd64.tar.gzcd /opt tar -zxvf ZenTaoPMS-21.2-zbox_amd64.tar.gz#启动 /opt/zbox/zbox start /opt/zbox/zbox…...

Java 网络原理 ①-IO多路复用 || 自定义协议 || XML || JSON
这里是Themberfue 在学习完简单的网络编程后,我们将更加深入网络的学习——HTTP协议、TCP协议、UDP协议、IP协议........... IO多路复用 ✨在上一节基于 TCP 协议 编写应用层代码时,我们通过一个线程处理连接的申请,随后通过多线程或者线程…...

Bash Shell知识合集
1. chmod命令 创建一个bash shell脚本 hello.sh ~script $ touch hello.sh脚本创建完成后并不能直接执行,我们要用chmod命令授予它可执行的权限: ~script $ chmod 755 hello.sh授权后的脚本可以直接执行: ~script $ ./hello.sh2.指定运行…...

从0入门自主空中机器人-1【课程介绍】
关于本课程: 本次课程是一套面向对自主空中机器人感兴趣的学生、爱好者、相关从业人员的免费课程,包含了从硬件组装、机载电脑环境设置、代码部署、实机实验等全套详细流程,带你从0开始,组装属于自己的自主无人机,并让…...

Doris使用注意点
自己学习过程中整理,非官方 dws等最后用于查询的表可以考虑使用row存储加快查询,即用空间换时间duplicate key的选择要考虑最常查询使用适当使用bloomfilter 加速查询适当使用aggregate 模式降低max,avg,min之类的计算并加快查询…...

Mybatis插件better-mybatis-generator的下载与使用
1.下载 找到设置 插件 搜索better-mybatis-generator 下载并且重启IDEA 2.连接数据库 点击测试连接 连接成功如下图 3.使用插件 选择对应的表 右击选择 注意:mysql8.0驱动一定要勾上mysql_8 其他地方不要动 然后实体类 mapper xml就都生成好了 mapper里有默认增删…...

uniapp小程序实现弹幕不重叠
uniapp小程序实现弹幕不重叠 1、在父组件中引入弹幕组件 <template><!-- 弹幕 --><barrage ref"barrage" class"barrage-content" reloadDanmu"reloadDanmu"></barrage> </template> <script>import barr…...

快速排序学习优化
首先,上图。 ‘’’ cpp int partSort(int *a ,int left,int right) {int keyi left; //做左侧基准while(left<right){while(left<right && a[right]>a[keyi]){right--;}while(left<right && a[left]<a[keyi]){left;}swap(a[left…...

微信流量主挑战:三天25用户!功能未完善?(新纪元4)
🎉【小程序上线第三天!突破25用户大关!】🎉 嘿,大家好!今天是我们小程序上线的第三天,我们的用户量已经突破了25个!昨天还是16个,今天一觉醒来竟然有25个!这涨…...

jetson 无显示器配置WIFI
我使用的 jetpack 版本是 6.1,发现自带 NetworkManager 软件包,此软件包包含一个守护程序、一个命令行界面(nmcli)和一个基于 curses 的界面(nmtui)。 可以使用 nmcli 命令配置wifi,nmcli 示例…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
