LeetCode--排序算法(堆排序、归并排序、快速排序)
排序算法
- 归并排序
- 算法思路
- 代码
- 时间复杂度
- 堆排序
- 什么是堆?
- 如何维护堆?
- 如何建堆?
- 堆排序
- 时间复杂度
- 快速排序
- 算法思想
- 代码
- 时间复杂度
归并排序
算法思路
归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成两个子数组的过程。另一个是治,它将两个有序数组合并成一个更大的有序数组。
将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。

代码
// 归并排序
public int[] sortArray(int[] nums) {return mergeSort(nums, 0, nums.length - 1);
}private int[] mergeSort(int[] nums, int left, int right) {// 递归终止条件if (left >= right) {// 返回单个元素的数组return new int[]{nums[left]};}// 分治int mid = (left 0+ right) / 2;// 分别对左右子数组进行排序int[] leftArr = mergeSort(nums, left, mid);int[] rightArr = mergeSort(nums, mid + 1, right);int[] res = new int[leftArr.length + rightArr.length];// 合并两个有序数组int i = 0, j = 0, k = 0;while (i < leftArr.length && j < rightArr.length) {if (leftArr[i] <= rightArr[j]) {res[k++] = leftArr[i++];} else {res[k++] = rightArr[j++];}}while (i < leftArr.length) {res[k++] = leftArr[i++];}while (j < rightArr.length) {res[k++] = rightArr[j++];}return res;
}
时间复杂度
O(nlogn)
堆排序
什么是堆?
如下图(大根堆)(二叉)堆是一个数组,它可以被看成一个完全二叉树。
二叉树形式:

数组形式:

堆的根节点在数组中的下标为0,我们很容易得到左孩子为1,右孩子为2,第i个节点的左孩子为2i+1,右孩子为2i+2 。
二叉堆分为两种形式:大根堆和小根堆。大根堆性质,根节点的值大于所以子树节点的值。小根堆性质,根节点的值小于所以子树节点的值。
如何维护堆?
Java代码维护大根堆:
//维护大根堆
private void heapify(int n,int i) {//当前根节点int largest = i;//左孩子节点int lchild = 2*i+1;//右孩子节点int rchild = 2*i+2;//找三个元素最大的作为父节点if (lchild < n && nums[lchild] > nums[largest]) {largest = lchild;}if (rchild < n && nums[rchild] > nums[largest]) {largest = rchild;}//如果交换则维护交换后的if (largest != i) {swap(largest,i);heapify(n,largest);}
}
问题:为啥交换后,只需要维护交换后的子节点呢?
举一个例子:

根节点需要跟左孩子交换,交换后,根节点的右子树并未改变树结构,则只需要递归维护根节点左子树的堆性质。
如何建堆?
我们可以用自低向上的方法利用上面维护堆的算法heapify来建堆。子数组从n/2开始都是树的叶子节点。每个叶子节点可以被看成包含一个元素的堆。所以建堆的过程从n/2-1–>0 。
//1.建堆//从最后一个有孩子的节点开始 n/2-1for (int i = n/2-1; i >= 0; i--) {heapify(n,i);}
堆排序
前面我们利用建堆算法成功建立一个大根堆。因为数组最大元素总在根节点nums[0]中,通过把它与nums[n-1]交换,我们可以让该元素放到正确的位置。这时候,如果我们从堆中去掉节点n-1,剩余节点中根的孩子结点仍然是大根堆,而新的根节点可能违背大根堆性质。为了维护大根堆性质,需要不断调用 heapify 从而在nums 上构建一个新的大根堆。堆排序算法会不断重复这个过程,直到堆的大小从n-1降到1 。
给出完整的堆排序算法:
private int[] nums;// 待排序数组
//堆排序
private void heap_sort(int n) {//1.建堆//从最后一个有孩子的节点开始 n/2-1for (int i = n/2-1; i >= 0; i--) {heapify(n,i);}//2.堆排序for (int i = n-1; i > 0; i--) {swap(i,0);//交换最后一个和根元素heapify(i,0);//交换后维护}
}
//维护大根堆
private void heapify(int n,int i) {int largest = i;int lchild = 2*i+1;int rchild = 2*i+2;//找三个元素最大的作为父节点if (lchild < n && nums[lchild] > nums[largest]) {largest = lchild;}if (rchild < n && nums[rchild] > nums[largest]) {largest = rchild;}//如果交换则维护交换后的if (largest != i) {swap(largest,i);heapify(n,largest);}
}private void swap(int i,int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}
时间复杂度
O(nlogn)
快速排序
算法思想
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
1、首先设定一个基数,通过该基数将数组分成左右两部分。
2、将大于或等于基数的数据集中到数组右边,小于基数的数据集中到数组的左边。此时,左边部分中各元素都小于或等于基数,而右边部分中各元素都大于或等于基数。
3、然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个基数,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
概括来说为 挖坑填数 + 分治法。
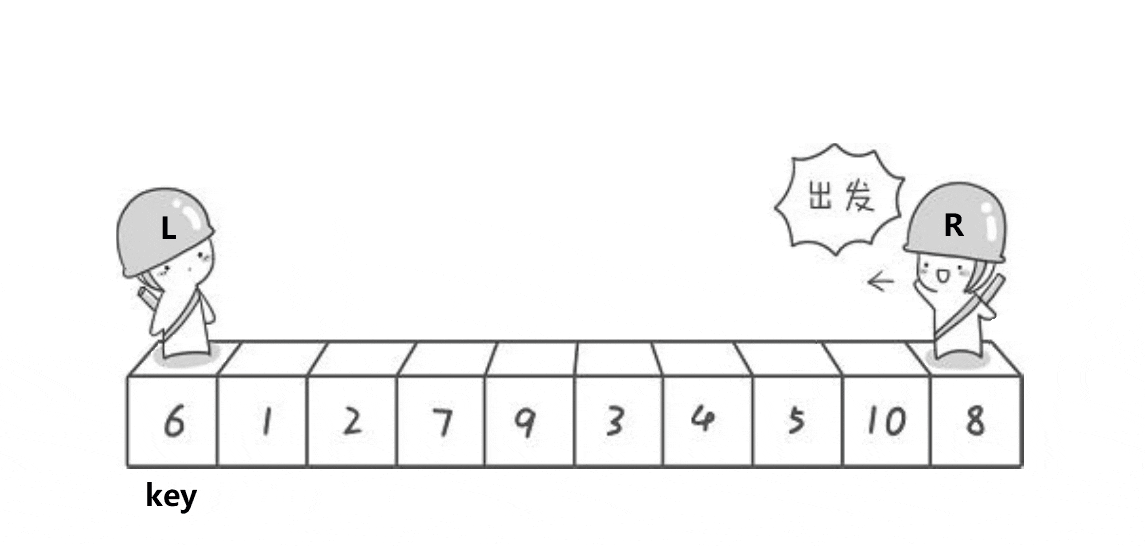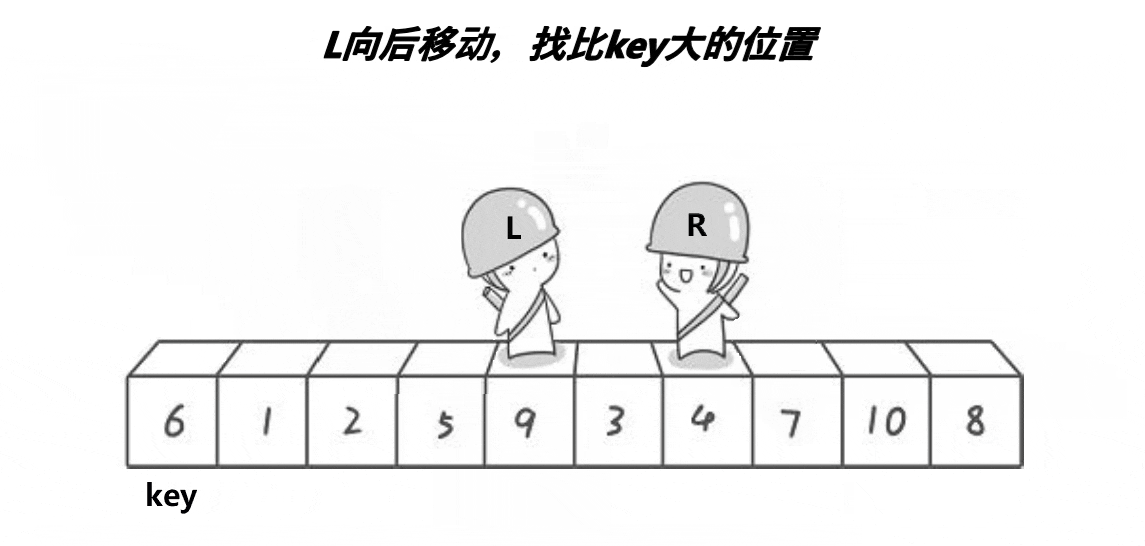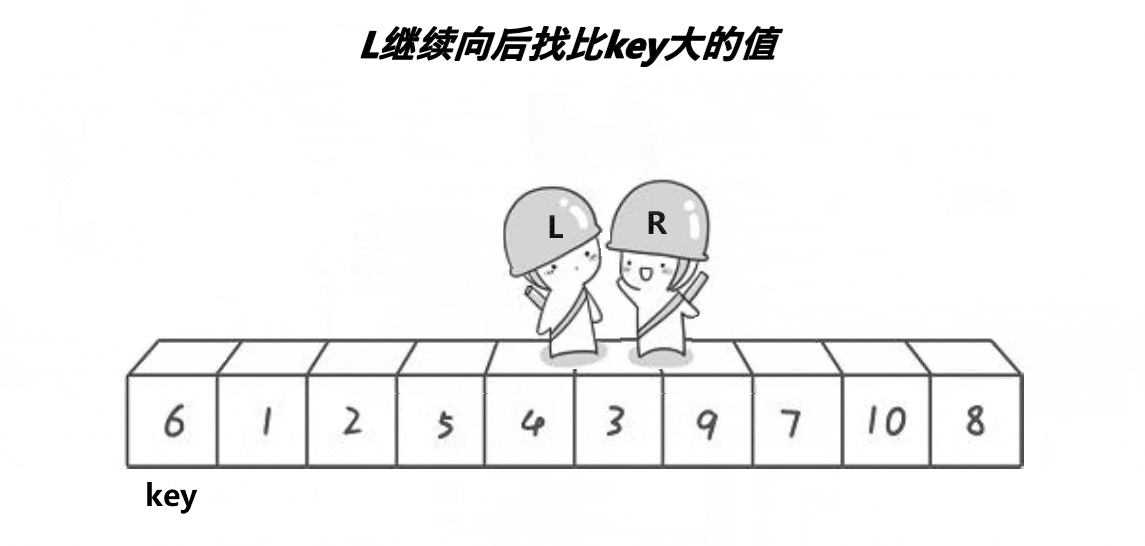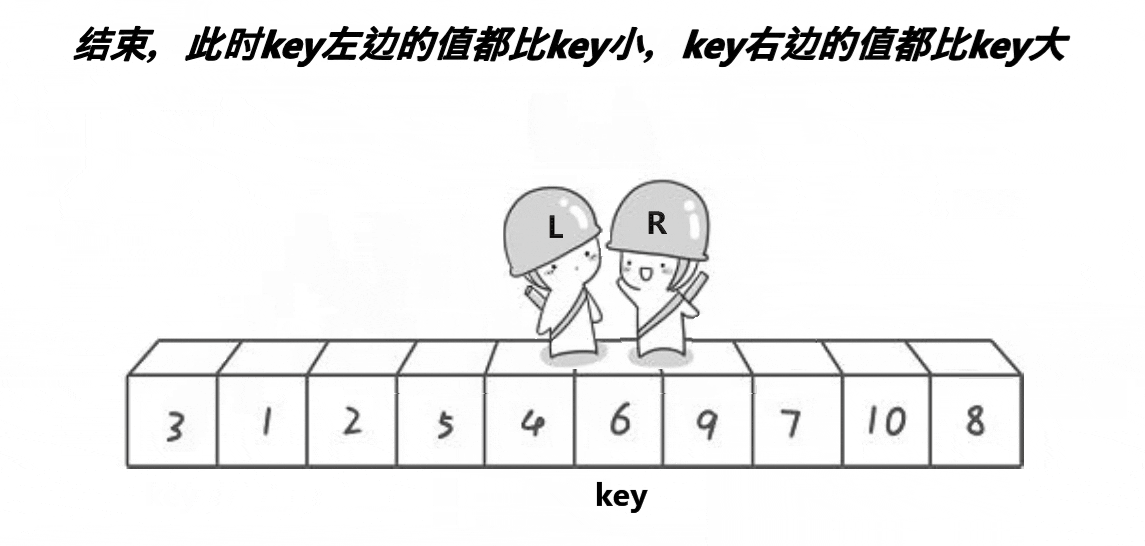
代码
代码中使用Random作为随机生成器生成基数,思想不变,只是基数选取的方式改变。
private int[] nums;
// 随机数生成器, 用于生成选择基数元素
private final Random random = new Random();public int[] sortArray(int[] nums) {this.nums = nums;quickSort(0, nums.length - 1);return nums;
}
public void quickSort(int left, int right) {// 递归终止条件if (left >= right) {return;}// 调用partition函数,对数组进行分区,并获取基准元素的最终位置int pivot = partition(left, right);// 递归调用,对左子数组进行快速排序quickSort(left, pivot - 1);// 递归调用,对右子数组进行快速排序quickSort(pivot + 1, right);
}
public int partition(int left, int right) {// 生成一个随机的基准元素位置int pivot = random.nextInt(right - left + 1) + left;// 保存基准元素的值int pivotVal = nums[pivot];// 将基准元素交换到数组的最后一个位置swap(pivot, right);// 定义两个指针,i指向数组的最左边,j指向数组的最右边int i = left, j = right;while (i < j) {// 从左向右找到第一个大于等于基准元素的位置while (i < j && nums[i] <= pivotVal) {i++;}// 从右向左找到第一个小于等于基准元素的位置while (i < j && nums[j] >= pivotVal) {j--;}// 如果i和j指向的位置不合法,则交换i和j指向的元素if (i < j) {swap(i, j);}}// 将基准元素交换到正确的位置swap(i, right);return i;
}public void swap(int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}
时间复杂度
O(nlogn)
相关文章:

LeetCode--排序算法(堆排序、归并排序、快速排序)
排序算法 归并排序算法思路代码时间复杂度 堆排序什么是堆?如何维护堆?如何建堆?堆排序时间复杂度 快速排序算法思想代码时间复杂度 归并排序 算法思路 归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成…...

华诺星空 Java 开发工程师笔试题 - 解析
单选题 1.Math.round(-11.5)等于多少?(B) A.-11.5 B.-11 C.-12 D.11.5 2.下列哪个没有继承自Collection接口。( C ) A.List B.Set C.Map D.全部 3.下列说法正确的有(B) A.在类方法中可用this来调用本类的类方法 B.在类方法中调用本类的类方法时可直接调用 C.在类…...

QT:一个TCP客户端自动连接的测试模型
版本 1:没有取消按钮 测试效果: 缺陷: 无法手动停止 测试代码 CMakeLists.txt cmake_minimum_required(VERSION 3.19) project(AutoConnect LANGUAGES CXX)find_package(Qt6 6.5 REQUIRED COMPONENTS Core Widgets Network)qt_standard_project_setup(…...

关于启动vue项目,出现:Error [ERR_MODULE_NOT_FOUND]: Cannot find module ‘xxx‘此类错误
目录 一、问题报错 二、原因分析 三、解决方法 一、问题报错 node环境变量配置有问题: (base) xxxM73H-15:~/VueProject/pproject-vue$ npm run dev /usr/bin/env: “node”: 没有那个文件或目录vue项目启动有问题: (base) xxx:~/VueProject/pproj…...

电路元件与电路基本定理
电流、电压和电功率 电流 1 定义: 带电质点的有序运动形成电流 。 单位时间内通过导体横截面的电量定义为电流强度, 简称电流,用符号 i 表示,其数学表达式为:(i单位:安培(A&#x…...

指针之矢:C 语言内存幽境的精准飞梭
一、内存和编码 指针理解的2个要点: 指针是内存中一个最小单元的编号,也就是地址平时口语中说的指针,通常指的是指针变量,是用来存放内存地址的变量 总结:指针就是地址,口语中说的指针通常指的是指针变量。…...

uniapp下载打开实现方案,支持安卓ios和h5,下载文件到指定目录,安卓文件管理内可查看到
uniapp下载&打开实现方案,支持安卓ios和h5 Android: 1、申请本地存储读写权限 2、创建文件夹(文件夹不存在即创建) 3、下载文件 ios: 1、下载文件 2、保存到本地,需要打开文件点击储存 使用方法&…...

免费干净!付费软件的平替款!
今天给大家介绍一个非常好用的电脑录屏软件,完全没有广告界面,非常的干净简洁。 电脑录屏 无广告的录屏软件 这个软件不需要安装,打开就能看到界面直接使用了。 软件可以全屏录制,也可以自定义尺寸进行录制。 录制的声音选择也非…...

软路由系统 iStoreOS 中部署 Minecraft 服务器
商业转载请联系作者获得授权,非商业转载请注明出处。协议(License): 知识共享署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0)作者(Author): lhDream链接(URL): https://blog.luhua.site/archives/1734968846131 软路由系统 iStoreOS 中部署 Minecraft…...
第 29 章 - ES 源码篇 - 网络 IO 模型及其实现概述
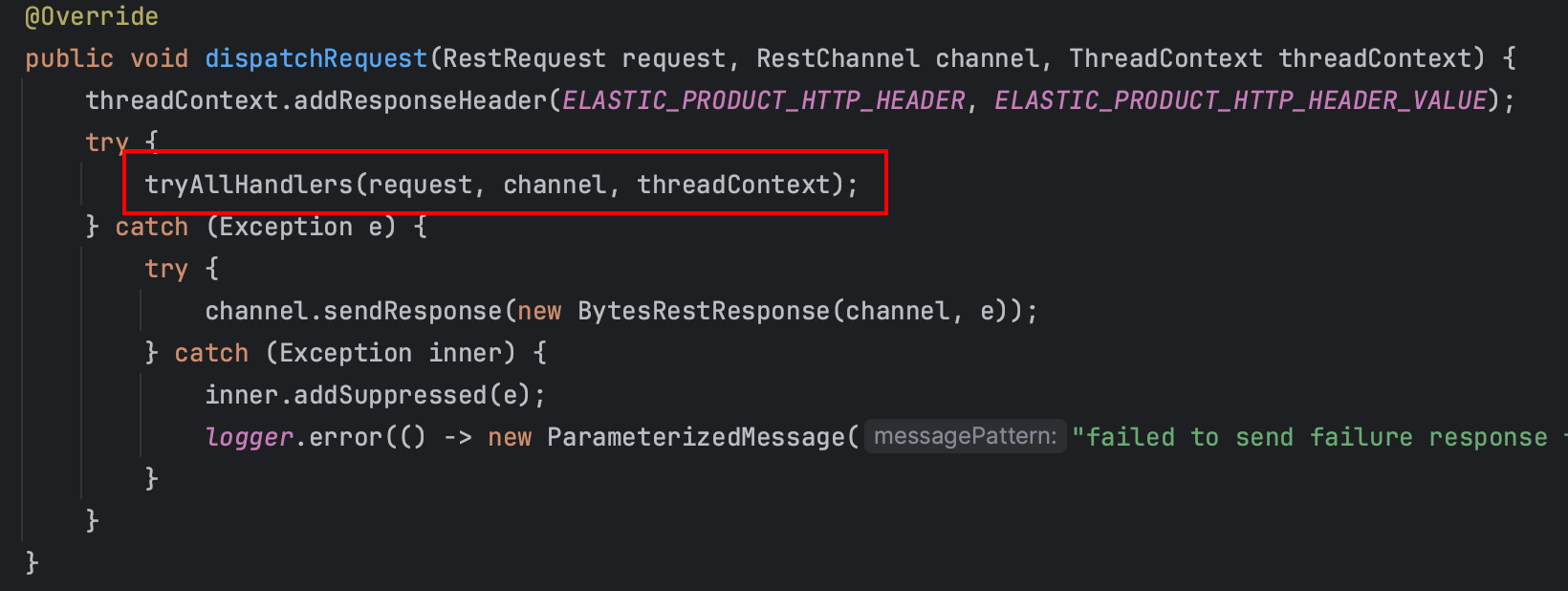
前言 本文介绍了 ES 使用的网络模型,并介绍 transport,http 接收、响应请求的代码入口。 网络 IO 模型 Node 在初始化的时候,会创建网络模块。网络模块会加载 Netty4Plugin plugin。 而后由 Netty4Plugin 创建对应的 transports࿰…...

细说STM32F407单片机IIC总线基础知识
目录 一、 I2C总线结构 1、I2C总线的特点 2、I2C总线通信协议 3、 STM32F407的I2C接口 二、 I2C的HAL驱动程序 1、 I2C接口的初始化 2、阻塞式数据传输 (1)函数HAL_I2C_IsDeviceReady() (2)主设备发送和接收数据 &#…...

从头开始学MyBatis—04缓存、逆向工程、分页插件
介绍了MyBatis的缓存、逆向工程和分页插件的使用 目录 1.Mybatis的缓存 1.1MyBatis的一级缓存 1.2MyBatis的二级缓存 1.3二级缓存的相关配置 1.4MyBatis缓存查询的顺序 1.5整合第三方缓存EHCache 1.5.1添加依赖 1.5.2各jar包功能 1.5.3创建EHCache的配置文件ehcache.x…...

Artec Space Spider助力剑桥研究团队解码古代社会合作【沪敖3D】
挑战:考古学家需要一种安全的方法来呈现新出土的陶瓷容器,对比文物形状。 解决方案:Artec Space Spider, Artec Studio 效果:本项目是REVERSEACTION项目的一部分,旨在研究无国家社会中复杂的古代技术。研究团队在考古地…...

《探索PyTorch计算机视觉:原理、应用与实践》
《探索PyTorch计算机视觉:原理、应用与实践》 一、PyTorch 与计算机视觉的奇妙相遇二、核心概念解析(一)张量:计算机视觉的数据基石(二)神经网络:视觉任务的智慧大脑(三)…...

【C#设计模式(21)——状态模式(State Pattern)】
前言 状态模式:在对象内部发生改变时改变其行为,使得对象在不同的状态下具有不同的行为表现。 代码 #region 状态模式-类/// 抽象 交通灯状态public abstract class TrafficLightState{public abstract void Display();}//红灯public class RedLight : TrafficLight…...

nvm日常使用中常用命令总结
日常开发vue项目中,不同的项目 我们可能需要安装不同的node版本,但是为了方便切换node,我们一般会安装一个名称为nvm的工具,这里总结一下,nvm常用的命令: 1、为了查看可用的 Node.js 版本,你可…...

【数据仓库】SparkSQL数仓实践
文章目录 集成hive metastoreSQL测试spark-sql 语法SQL执行流程两种数仓架构的选择hive on spark数仓配置经验 spark-sql没有元数据管理功能,只有sql 到RDD的解释翻译功能,所以需要和hive的metastore服务集成在一起使用。 集成hive metastore 在spark安…...

PessimisticLock
想象你和你的朋友都想去图书馆借同一本非常受欢迎的小说。为了确保你们中的一位能够成功借到这本书,图书馆采用了悲观锁机制来管理借阅过程。 悲观锁的方式 查看书籍状态:当你到达图书馆并决定要借这本小说时,你先告诉图书管理员你想借这本…...

【Maven】属性管理
1. 属性 问题导入 定义属性有什么好处? 1.1 属性配置与使用 ①:定义属性 <!--定义自定义属性--> <properties><spring.version>5.2.10.RELEASE</spring.version><junit.version>4.12</junit.version> </prop…...

微信小程序性能优化、分包
性能优化是任何应用开发中的重要组成部分,尤其是在移动环境中。对于微信小程序而言,随着用户量的增加和应用功能的丰富,性能优化显得尤为关键。良好的性能不仅提升用户体验,还能增加用户留存率和应用的使用频率。我们将探讨如何在…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
