【算法】复杂性理论初步
六、算法复杂性初步
重要的复杂性类
-
P P P 的定义
-
多项式时间内可解的问题
-
若 L ∈ P L∈P L∈P,则存在确定性多项式时间的图灵机 M M M,使得
M ( x ) = 1 ⟺ x ∈ L M(x)=1⟺x∈L M(x)=1⟺x∈L
-
-
N P NP NP 的定义
-
多项式时间内可验证验证解的正确性
-
(表示非确定性多项式时间而不是非多项式时间)
-
若 L ∈ N P L∈NP L∈NP,则存在确定性多项式时间的图灵机 M M M,使得
x ∈ L ⟺ ∃ w ∈ { 0 , 1 } p l o y ( n ) s . t . M ( x , w ) = 1 x∈L⟺\exist w∈\{0,1\}^{ploy(n)}\ \ s.t.\ M(x,w)=1 x∈L⟺∃w∈{0,1}ploy(n) s.t. M(x,w)=1
注:如果 x ∈ L x∈L x∈L,那么存在一个证书 w w w,使 M M M能够在多项式时间内验证 x ∈ M x∈M x∈M
-
-
N P − h a r d NP-hard NP−hard
- 若一个问题属于 N P − h a r d NP-hard NP−hard,那么它可以在多项式时间内规约成 N P NP NP 问题
-
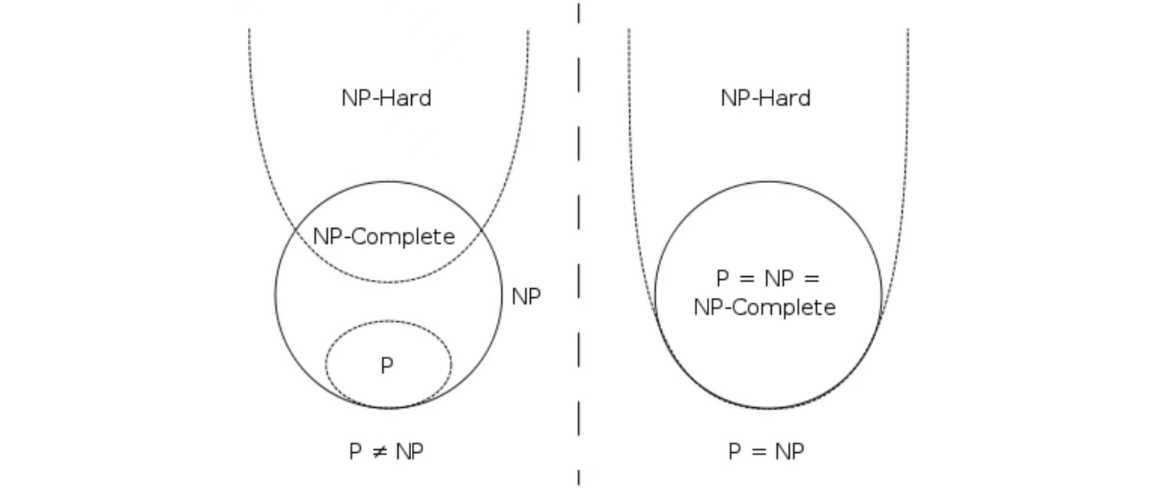
N P − c o m p l e t e NP-complete NP−complete
- 是 N P NP NP和 N P − h a r d NP-hard NP−hard的交集,即 N P C = N P ∩ N P H NPC=NP∩NPH NPC=NP∩NPH
- N P C NPC NPC是 N P NP NP中最难的问题,如果找到多项式时间解决 N P C NPC NPC,那么 P = N P P=NP P=NP
SAT 问题
定义:给定一个布尔逻辑表达式,判断是否存在一个布尔变量赋值,使得整个表达式的值为真。
合取范式(CNF):一种布尔逻辑表达式的标准化形式,若干个句子合取(AND),每个句子中若干个文字析取(OR)
例如,以下一个CNF公式:
( ¬ a 1 ∨ a 2 ) ∧ ( ¬ a 1 ∨ a 3 ∨ a 4 ) ∧ ( a 1 ∨ ¬ a 2 ∨ a 3 ∨ ¬ a 4 ) (\neg a_1 \lor a_2) \land (\neg a_1 \lor a_3 \lor a_4) \land (a_1 \lor \neg a_2 \lor a_3 \lor \neg a_4) (¬a1∨a2)∧(¬a1∨a3∨a4)∧(a1∨¬a2∨a3∨¬a4)
注:存在一种赋值,使其中一个句子为真,整个CNF即为真。
2-SAT问题:每个子句恰好包含2个文字。 P P P 类问题。
3-SAT问题:每个子句恰好包含3个文字。 N P − c o m p l e t e NP-complete NP−complete 问题。
- 例如: ( l 1 ∨ l 2 ∨ l 3 ) ∧ ( l 4 ∨ l 5 ∨ l 6 ) ∧ ⋯ (l_1 \lor l_2 \lor l_3) \land (l_4 \lor l_5 \lor l_6) \land \cdots (l1∨l2∨l3)∧(l4∨l5∨l6)∧⋯
当n>2,n-SAT问题就是NP-hard的。任何n-SAT都可以通过引入新变量的方法转化为3-SAT问题。
随机化算法
ZPP类型
- 保证一定能找到正确答案
- 需要多次运行,可以在期望的多项式时间内找到结果
- 即:保证正确性,运行时间随机性
- 如:随机化快速排序、随机化选择算法
BPP类型
- 不保证得到正确答案,结果可能出错
- 时间是确定的多项式时间
- 即:时间复杂度好,结果不好
- 如:矩阵恒等式测试
6.1 证明: P ⊆ N P P⊆NP P⊆NP
证明:
- 对于 P P P问题的图灵机 M M M,构造另一个图灵机 M ′ M' M′:输入是 w w w和 x x x,对于相同的 x x x有相同的输出, w w w对输出无影响
- 当 x ∈ L x∈L x∈L时, M ( x ) = 1 M(x)=1 M(x)=1,存在 w ′ ∈ 0 , 1 p l o y ( n ) w'∈{0,1}^{ploy(n)} w′∈0,1ploy(n), M ′ ( x , w ′ ) = 1 M'(x,w')=1 M′(x,w′)=1
- 当 x ∉ L x ∉L x∈/L时, M ( x ) = 0 M(x)=0 M(x)=0,对于任意的 w w w, M ′ ( x , w ) = 0 M'(x,w)=0 M′(x,w)=0
- 显然 M ′ M' M′是确定性多项式图灵机,结合 N P NP NP问题定义,存在 w ′ ∈ 0 , 1 p l o y ( n ) w'∈{0,1}^{ploy(n)} w′∈0,1ploy(n), M ′ ( x , w ′ ) = 1 M'(x,w')=1 M′(x,w′)=1,验证解是否正确。所以该 P P P问题也是一个 N P NP NP问题,所以 P ⊆ N P P⊆NP P⊆NP。
6.2 证明: 如果存在 N P NP NP 难的问题 Π ∈ P Π ∈ P Π∈P,则 P = N P P = NP P=NP
证明:
- 根据 Π ∈ P Π ∈ P Π∈P,得 Π Π Π在多项式时间可解决
- 根据 N P − h a r d NP-hard NP−hard 定义,所有 N P NP NP问题 F F F可在多项式时间内规约到 Π Π Π,即 F ∈ N P F∈NP F∈NP,有 F ≤ p Π F≤_pΠ F≤pΠ
- 所以 F F F在多项式时间转化为 Π Π Π,再多项式求解 Π Π Π,整个过程是多项式时间完成的,所以 N P ⊆ P NP⊆P NP⊆P
- 又已知 P ⊆ N P P⊆NP P⊆NP,所以证得 P = N P P=NP P=NP。
6.3 证明:如果 N P = P NP=P NP=P,则单向陷门不存在。
- 假设算法
Invert用来寻找函数 f f f的逆映射:利用一系列语言 L i Li Li,表示是否存在 w w w使得 y = f ( z ∣ ∣ w ) y=f(z||w) y=f(z∣∣w) - 根据文本内容, L i Li Li属于 N P NP NP,同依据条件,也属于 P P P
- 如果 P = N P P=NP P=NP,那么该算法能在多项式内求解,即找到了函数 f f f的逆映射,也就是找到 x x x使得 f ( x ) = y f(x)=y f(x)=y
- 综上,若 N = N P N=NP N=NP,多项式时间可破坏单项函数的不可逆的性质,则单向陷门不存在
相关文章:

【算法】复杂性理论初步
六、算法复杂性初步 重要的复杂性类 P P P 的定义 多项式时间内可解的问题 若 L ∈ P L∈P L∈P,则存在确定性多项式时间的图灵机 M M M,使得 M ( x ) 1 ⟺ x ∈ L M(x)1⟺x∈L M(x)1⟺x∈L N P NP NP 的定义 多项式时间内可验证验证解的正确性 &…...

HarmonyOS NEXT应用开发实战:免费练手的网络API接口分享
学习一项技能,最好也最快的办法就是直接动手实战。在实战中不断的总结经验和收获成就感。这里分享些好用且免费的网络API练手接口,这对于想要提升自己网络开发能力的开发者来说,无疑是极大的福音。今天,我将详细介绍一个API接口集…...

C++的第一个程序
前言 在学习c之前,你一定还记得c语言的第一个程序 当时刚刚开始进行语言学习 因此告诉到,仅仅需要记住就可以 #include <stdio.h>int main(){printf("Hello World");return 0; }而对于c中的第一个程序,似乎有所变化 C的…...

Java 中 Stream 流的使用详解
Java 中 Stream 流的使用详解 什么是 Stream? Stream 是 Java 8 引入的一种全新的操作集合的方式。它支持通过声明性方式对集合进行复杂的数据操作(如过滤、排序、聚合等),避免使用大量的 for 循环,提高代码的可读性…...
【UE5.3.2】生成vs工程并rider打开
Rider是跨平台的,UE也是,当前现在windows上测试首先安装ue5.3.2 会自动有右键的菜单: windows上,右键,生成vs工程 生成的结果 sln默认是vs打开的,我的是vs2022,可以open with 选择 rider :Rider 会弹出 RiderLink是什么插...

ssh免密码登陆配置
ssh 命令本身不支持直接在命令中带上密码,出于安全考虑,SSH 协议不允许将密码明文写在命令中。直接在命令行中输入密码是一种不推荐的做法,因为它会暴露密码,增加安全风险。 如果你希望实现自动化登录而不手动输入密码࿰…...

Hive之import和export使用详解
在hive-0.8.0后引入了import/export命令。 Export命令可以导出一张表或分区的数据和元数据信息到一个输出位置,并且导出数据可以被移动到另一个hadoop集群或hive实例,并且可以通过import命令导入数据。 当导出一个分区表,原始数据可能在hdf…...

数据库锁的深入探讨
数据库锁(Database Lock)是多用户环境中用于保证数据一致性和隔离性的机制。随着数据库系统的发展,特别是在高并发的场景下,锁的机制变得尤为重要。通过使用锁,数据库能够防止并发操作导致的数据冲突或不一致。本文将深…...

【每日学点鸿蒙知识】沉浸式状态栏、类似ref 属性功能属性实现、自定义对话框背景透明、RichEditor粘贴回调、自动滚动列表
1、HarmonyOS 沉浸式状态栏? 实现沉浸式状态栏功能时,能够实现,但是目前每个自定义组件都需要padding top 状态栏的高度才行,有办法实现统一设置吗?不需要每个自定义组件中都padding top 状态栏的高度? 暂…...
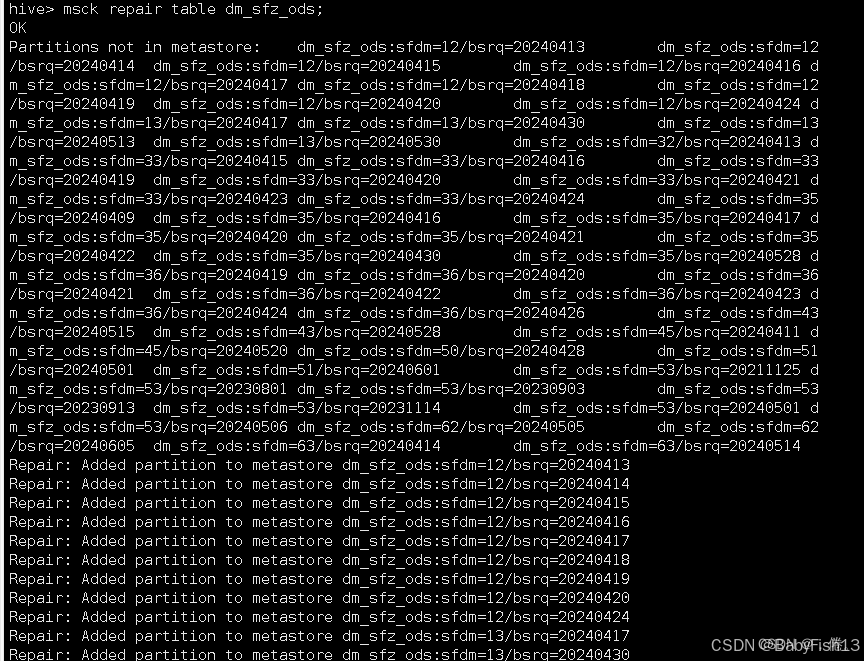
Hive刷分区MSCK
一、MSCK刷分区 我们平时通常是通过alter table add partition方式增加Hive的分区的,但有时候会通过HDFS put/cp命令或flink、flum程序往表目录下拷贝分区目录,如果目录多,需要执行多条alter语句,非常麻烦。Hive提供了一个"…...

在Ubuntu下通过Docker部署Mastodon服务器
嘿,朋友们,今天咱们来聊聊如何在Ubuntu上通过Docker部署Mastodon服务器。想要拥有自己的社交媒体平台?Mastodon就是个不错的选择!🌐🚀 Docker与Mastodon简介 Docker是一个开源的容器化平台,让…...
【EtherCATBasics】- KRTS C++示例精讲(2)
EtherCATBasics示例讲解 目录 EtherCATBasics示例讲解结构说明代码讲解 项目打开请查看【BaseFunction精讲】。 结构说明 EtherCATBasics:应用层程序,主要用于人机交互、数据显示、内核层数据交互等; EtherCATBasics.h : 数据定义…...

MYSQL无法被连接问题
如果您在尝试连接到MySQL服务器时遇到问题,以下描述了您可以采取的一些措施来纠正该问题。 确保服务器正在运行。如果没有,则客户端无法连接到它。例如,如果尝试连接到服务器失败并出现以下消息之一,则可能是服务器未运行…...
?)
【Python】什么是字典(Dictionary)?
什么是字典(Dictionary)? 字典(Dictionary)是 Python 中一种 可变(mutable)的数据结构,用于存储键值对(key-value pairs)。字典通过 键(key&…...

Web安全 - API 成批分配漏洞的四种修复方案
文章目录 概述危害修复建议与实施方案解决方案 1:手动绑定数据解决方案 2:使用 DTO 进行数据过滤解决方案 3:启用字段白名单解决方案 4:验证输入数据模式 验证修复有效性小结 概述 批量分配漏洞(Mass Assignment&#…...

计算机网络实验室建设方案
一、计算机网络实验室拓扑结构 计算机网络综合实验室解决方案,是面向高校网络相关专业开展教学实训的综合实训基地解决方案。教学实训系统采用 B/S架构,通过公有云教学实训平台在线学习模式,轻松实现网络系统建设与运维技术的教学…...

ubuntu20.04 调试bcache源码
搭建单步调试bcache的环境,/dev/sdb作为backing dev, /dev/sdc作为cache dev。 一、宿主机环境 1)安装ubuntu 20.04 : 参考ubuntu20.04 搭建kernel调试环境第一篇--安装系统_ubuntu kernel-CSDN博客安装,其中的第六…...

xss csrf怎么预防?
一、XSS(跨站脚本攻击)预防 XSS 是指攻击者向目标网站注入恶意脚本,从而在用户浏览器中执行。 1. 输入过滤 清理用户输入: 拦截或清理HTML特殊字符(如 <, >, , ", &)。使用安全库&#x…...
:Prompt +Bert-MLM(FT))
near-synonym反义词生成(2):Prompt +Bert-MLM(FT)
near-synonym之反义词生成方法二 near-synonym, 中文反义词/近义词/同义词(antonym/synonym)工具包. 方法一为(neg_antonym): Word2vec -> ANN -> NLI -> Length 方法二为(mlm_antonym): Prompt Bert-MLM(FT) Beam-Search 项目地址 github: https://github.com/yon…...

【服务器项目部署】⭐️将本地项目部署到服务器!
目录 🍸前言 🍻一、服务器选择 🍹 二、服务器环境部署 2.1 java 环境部署 2.2 mysql 环境部署 🍸三、项目部署 3.1 静态页面调整 3.2 服务器端口开放 3.3 项目部署 🍹四、测试 🍸前言 小伙伴们大家好…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
