AtCoder Grand Contest 061(题解)
A - Long Shuffle
这道题本质是一个找规律的题
既然是打表题,我们先暴力把他打出来

(盗一张图.jpg)
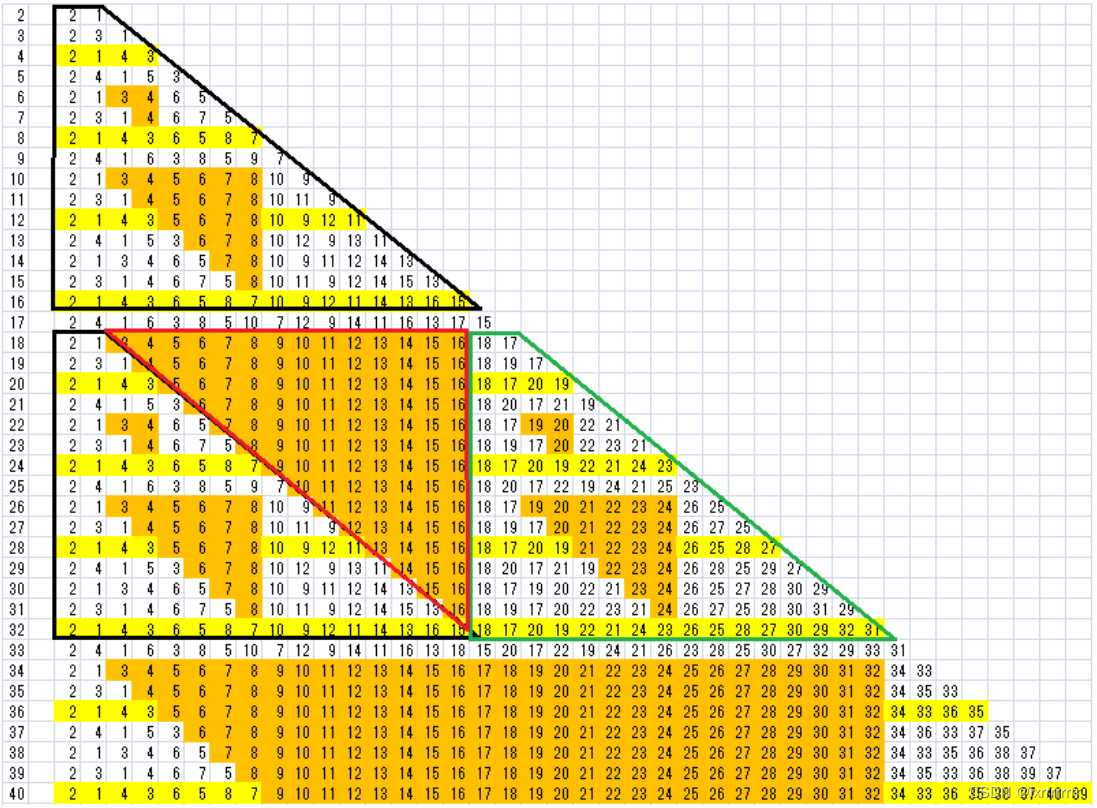
接下来就是在这张图中挖掘答案
我们可以明显的看到偶数行是有一些规律的
要么是相邻对的互换,要么不变
不变和互换的位置也有讲究,在二进制下可以发现这样的规律

这里的n和k代表第n行的第k个数
我们发现偶数行完全满足这个公式
而对于奇数行,看起来没什么规律
我们可以联系n-1行,也就是奇数行对应的上一个偶数行
可以发现对于奇数行A(i,j),满足A(i,j)=A(i-1,A(i-1,j-1)+1) 当j大于1且小于n
代码如下:
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fer(i,a,b) for(int i=a;i<=b;++i)
#define der(i,a,b) for(int i=a;i>=b;--i)
#define all(x) (x).begin(),(x).end()
#define pll pair<int,int>
#define et cout<<'\n'
#define xx first
#define yy second
using namespace std;
int A[105];
void go(int l, int r) {if (l + 1 == r) {swap(A[l], A[r]);}else {go(l, r - 1);go(l + 1, r);}
}//暴力
int back(int n, int k) {k--;int block = k / 2;int F = n / 2 - 1;if ((F & block) == block) {k ^= 1;}return k + 1;
}
signed main() {ios_base::sync_with_stdio(false);cin.tie(0);int tst;cin >> tst;while (tst--) {int n, k;cin >> n >> k;if (n % 2 == 1) {if (k > 1) {k = back(n - 1, k - 1);k++;}if (k <= n - 1) {k = back(n - 1, k);}cout << k << '\n';}else {int f1 = back(n, k);cout << f1 << '\n';}}return 0;
}B - Summation By Construction
这道题就很玄学
除了2是NO,其他都是YES
其中一种解决方式是
我们可以用对角线的思路来构建
比如
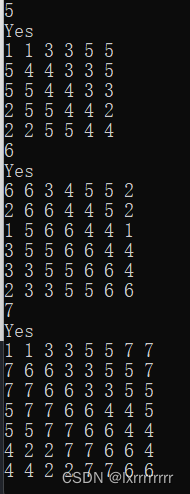
代码如下
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fer(i,a,b) for(int i=a;i<=b;++i)
#define der(i,a,b) for(int i=a;i>=b;--i)
#define all(x) (x).begin(),(x).end()
#define pll pair<int,int>
#define et cout<<'\n'
#define xx first
#define yy second
using namespace std;
constexpr int max_n=100;
int a[max_n+1][max_n+2];
void test(){int n;cin>>n;if(n==2){puts("No");return;}puts("Yes");if((n&1)){int m=n+1;for(int i=1; i<=n; i+=2){int now=i;for(int j=1; j<=n; ++j){int col=j<=i?i:(n-i);a[j][now]=col;++now>m&&(now=1);a[j][now]=col;}}for(int i=1; i<=n; ++i){for(int j=1; j<=n; ++j)cout<<a[i][j]<<" ";cout<<a[i][m]<<'\n';}return;}const int m=n+1;for(int i=1; i<=n; ++i)a[i][i]=a[i][i+1]=n;for(int j=2; j<=n; ++j)a[j%n+1][j]=a[(j+1)%n+1][j]=n-1;a[2][1]=a[n][1]=a[2][m]=a[1][m]=2;a[3][1]=a[3][m]=1;for(int i=3,ed=n-3; i<=ed; i+=2){int now=i+1;for(int j=1; j<=m; ++j){const int col=j<=i?i:(m-i);a[now][j]=col;++now>n&&(now=1);a[now][j]=col;}}for(int i=1; i<=n; ++i){for(int j=1; j<=n; ++j)cout<<a[i][j]<<" ";cout<<a[i][m]<<'\n';}
}
signed main(){int t;cin>>t;while(t--){test();}return 0;
}相关文章:

AtCoder Grand Contest 061(题解)
A - Long Shuffle 这道题本质是一个找规律的题 既然是打表题,我们先暴力把他打出来 (盗一张图.jpg) 接下来就是在这张图中挖掘答案 我们可以明显的看到偶数行是有一些规律的 要么是相邻对的互换,要么不变 不变和互换的位置也有讲究,在二进制…...
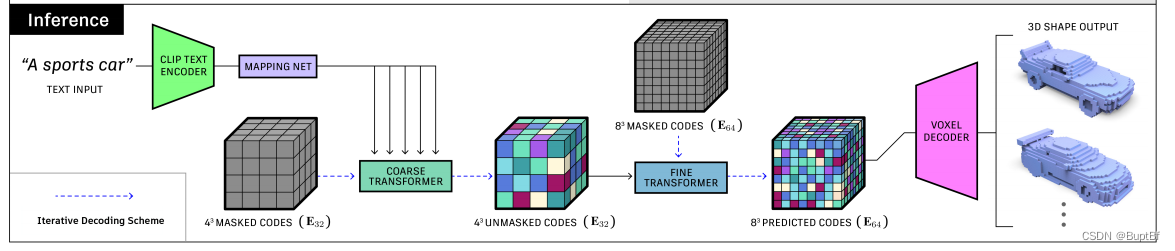
生成系列论文:文本控制的3d点云生成 TextCraft(一):论文概览
TextCraft: Zero-Shot Generation of High-Fidelity and Diverse Shapes from Text 论文原文: https://arxiv.org/abs/2211.01427 论文的研究动机 DALL2已经在文本控制的图像生成上取得很好的效果,但是基于文本控制的3d点云生成的研究还不太成熟&#…...

IDEA常用插件
常用IDEA插件 Codota 插件下载地址:Codota AI Autocomplete for Java and JavaScript - IntelliJ IDEs Plugin | Marketplace IDEA的自动补全功能已经很强大了,但是这个插件的自动补全功能更加强大,这是一个基于AI技术,学习了大量…...
Spring的事务传播机制
多个事务方法相互调用时,事务如何在这些方法之间进行传播,Spring中提供了七种不同的传播机制,来保证事务的正常执行: REQUIRED:默认的传播机制,如果存在事务,则支持/加入当前事务,如…...
Python:路径之谜(DFS剪枝)
题目描述 小张冒充 X 星球的骑士,进入了一个奇怪的城堡。 城堡里边什么都没有,只有方形石头铺成的地面。 假设城堡地面是 nn 个方格。如下图所示。 按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走…...
阿里巴巴在开源压测工具 JMeter 上的实践和优化
Apache JMeter [1] 是 Apach 旗下的开源压测工具,创建于 1999 年初,迄今已有超过 20 年历史。JMeter 功能丰富,社区(用户群体)庞大,是主流开源压测工具之一。 性能测试通常集中在新系统上线或大型活动前&…...

React Draggable插件实现拖拽功能
React Draggable插件实现拖拽功能1.下载Draggable插件2.引入Draggable插件3.设置一个div,并设置样式,并用Draggable包裹起来4.设置拖拽的范围5.Draggable常用props1.下载Draggable插件 npm install react-draggable2.引入Draggable插件 // 引入拖拽插件…...

MySQL-运算符
算术运算符: 加法运算-: 减法运算*: 乘法运算/: 除法运算,返回商%: 求余运算,返回余数例:创建n5表,插入数字100,查看数据表分别查看、-、*、/、%mysql> create table n5(-> num int); Query OK, 0 rows affected…...
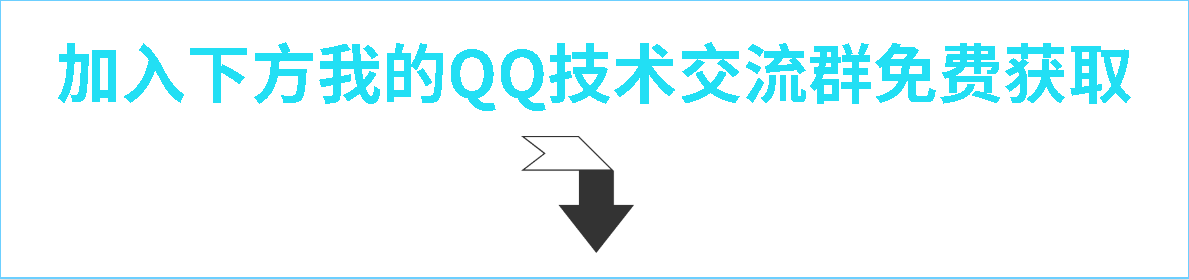
Hudi-基本概念(时间轴、文件布局、索引、表类型、查询类型、数据写、数据读、Compaction)
文章目录基本概念时间轴(TimeLine)文件布局(File Layout)Hudi表的文件结构Hudi存储的两个部分Hudi的具体文件说明索引(Index)原理索引选项全局索引与非全局索引索引的选择策略对事实表的延迟更新对事件表的去重对维度表的随机更删…...
)
数据分享|中国各省、各市、各区县分年、分月、逐日平均气温数据(2000年~2019年)
今天分享给大家的是 2000 年~2019 年中国各省、各市、各县的分年、分月、逐日的平均气温数据(单位:摄氏度) 原始数据来源于国家气象科学数据共享服务平台-中国地面气候资料日值数据集(V3.0),原始数据是各个观测站点的日度数据,为了方便大家使用,我使用 Barnes 方法(…...

steam/csgo搬砖,2023年最暴利的项目
这个项目赚钱主要来源于两个地方: 1.比如说今天美元的汇率是1美元6.8人民币,那我们有特定的渠道能拿到1美元5.0-5.5左右人民币的价格,100美元的汇率差利润就有180元左右的利润,当然这个价格是根据国际的汇率上下会有浮动的。 2.…...

RDSDRDSPolarDBPolarDB-X的区别
RDS 阿里云关系型数据库(Relational Database Service,简称RDS),是一种稳定可靠、可弹性伸缩的在线数据库服务。 基于阿里云分布式文件系统和高性能存储,RDS支持MySQL、SQL Server、PostgreSQL和PPAS(Post…...

【Python学习笔记】30.Python3 命名空间和作用域
前言 本章介绍Python的命名空间和作用域。 命名空间 先看看官方文档的一段话: A namespace is a mapping from names to objects.Most namespaces are currently implemented as Python dictionaries。 命名空间(Namespace)是从名称到对象的映射,大…...

后量子 KEM 方案:Kyber
参考文献: Bos J, Ducas L, Kiltz E, et al. CRYSTALS-Kyber: a CCA-secure module-lattice-based KEM[C]//2018 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 2018: 353-367.Avanzi R, Bos J, Ducas L, et al. Crystals-kyber[J]. NIST…...
2019年广东工业大学腾讯杯新生程序设计竞赛(同步赛)
同步赛链接 A-原初的信纸(最值,STL) 题意: 找 n 个数的最大值. 参考代码: void solve() {int n;std::cin >> n;std::vector<int> a(n);for (auto &c : a)std::cin >> c;std::cout << *max_element…...

生产Nginx现大量TIME-WAIT,连接耗尽,该如何处理?
背景说明: 在尼恩读者50交流群中,是不是有小伙伴问: 尼恩,生产环境 Nginx 后端服务大量 TIME-WAIT , 该怎么办? 除了Nginx进程之外,还有其他的后端服务如: 尼恩,生产环境…...
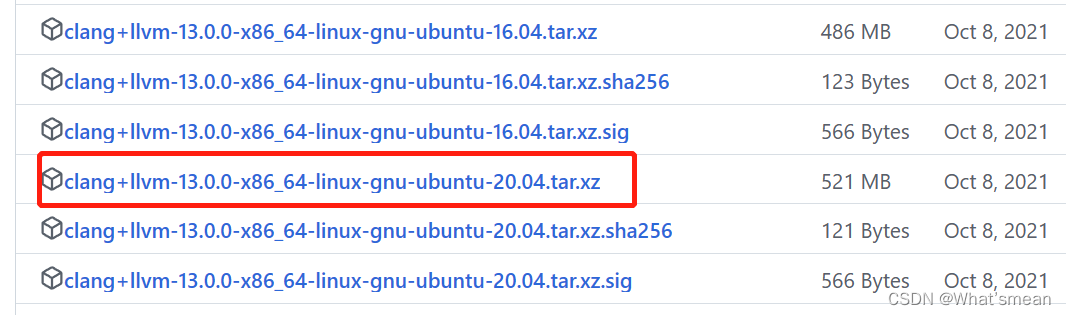
Linux服务器clang-13安装(环境变量配置)
1.从llvm的github网址选择合适的release合适的运行平台进行下载,下载官方预编译的二进制压缩包。 2.将下载好的压缩包进行本地上传。 使用scp命令进行上传 scp -r -P 端口号 本地文件路径 服务器ID等:服务器上目标地址 3.解压(tar命令) 4.环境变量配…...
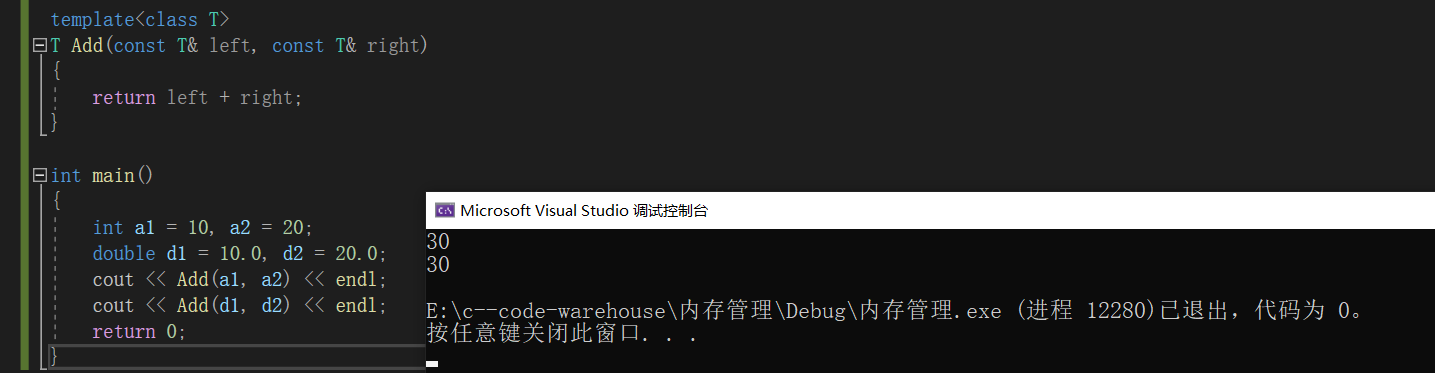
【C++】C/C++内存管理模板初阶
文章目录一、 C/C内存管理1. C/C内存分布2. C内存管理方式3. operator new与operator delete函数4. new和delete的实现原理5. 定位new表达式6. 常见面试题malloc/free和new/delete的区别内存泄漏二、模板初阶1. 泛型编程2. 函数模板3. 类模板一、 C/C内存管理 1. C/C内存分布 …...

笙默考试管理系统-index展示
public class PageList<T> : List<T> { public int PageIndex { get; private set; } //页索引 public int PageSize { get; private set; }//页大小 public int TotalPage { get; private set; }//总页数 public int TotalCo…...
前端基础知识6
谈谈你对语义化标签的理解语义化标签就是具有语义的标签,它可以清晰地向我们展示它的作用和用途。 清晰的代码结构:在页面没有css的情况下,也能够呈现出清晰的代码内容 有利于SEO: 爬虫依赖标签来确定关键字的权重,因此可以和搜索…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

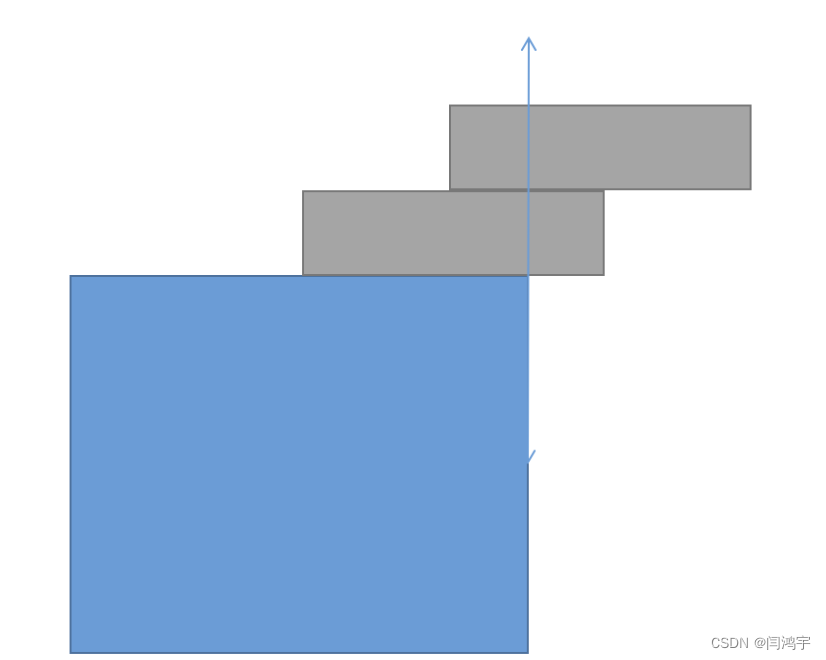
OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
