数据结构复习 (二叉查找树,高度平衡树AVL)
1.二叉查找树:
为了更好的实现动态的查找(可以插入/删除),并且不超过logn的时间下达成目的
定义: 二叉查找树(亦称二叉搜索树、二叉排序树)是一棵二叉树,其各结点关键词互异,且中根序列按其关键词递增排列。
等价描述: 二叉查找树中任一结点P,其左子树中结点的关键词都小于P的关键词,右子树中结点的关键词都大于P的关键词,且结点P的左右子树也都是二叉查找树。
节点:
BTSTreenode,有左右子树,有键值
有的操作是:
查找,插入和删除,
其他的创建和排序都可以通过上述完成
1,查找:
通过和当前的节点比较大小,来确定之后是:F.返回答案S.去更小的左边,T.去更大的右边
BSTnode* Search(BSTnode* root, int K){
if (root == NULL || root->key == K) return root;
if (K < root->key) return Search(root->left, K);
else return Search(root->right, K);
}
2,插入
根据和左右比较的方法来选择左边还是右边插入,但是不会插入相同的节点
可以引用实现,也可以是返回值实现
引用:
void insert(node*& root,int k){
If(root==NULL||root->val==k){
root=new node(k);
Return;
}
If(k>root->k)insert(root->left,k);
Else insert(root->right,k);
}
返回:
node* insert(node* root,int k){
If(root==NULL)return new node(k);
If(root->val==k)return root;
If(root->val>k)root->right=insert(root->right,k);
Else root->left=insert(root->left,k);
Return root;
}
3,删除,就是通过查找,然后判断:
,没有子树,直接删除
,有一个子树,直接上提
,两个子树,让右边最小的节点s上提到当前位置,之后删除S
void remove(BSTnode* &root, int K) {
if(root==NULL) return;
if(K<root->key) remove(root->left, K); //在左子树删K
else if(K>root->key) remove(root->right, K); //在右子树删K
else if(root->left!=NULL && root->right!=NULL){ //非根节点删除
BSTnode *s=root->right;
while(s->left!=NULL) s=s->left;
root->key=s->key; //s为t右子树中根序列第一个结点
remove(root->right, s->key);
}
else{ //根节点删除
BSTnode* oldroot=root;
root=(root->left!=NULL)? root->left:root->right;
delete oldroot;
}
}
numofBST
F[i]=f[i-1]*(4*i-2)/(i+1)
二叉查找树总结
➢则由n个互异关键词随机生成的二叉查找树,平均高度为O(logn)
➢查找、插入、删除平均时间复杂度O(logn),但最坏情况时间复杂度为O(n)
2,高度平衡树:(AVL)
为了防止出现二叉查找树发生左/右偏的情况出现的,让一个树的左右高度相差不大于1
平衡系数:左子树高度-右子树高度
高度为h的AVL至少有

所以n>=2^(h/2),同理,h<=2logn
一颗AVL平均比完全二叉树高44%
节点AVLnode 记录的信息是键值,高度,左右子树
初始的时候每个节点的高度是0,空节点的高度为-1
具体操作:
1,计算高度
Int update_H(node* t){
If(t==NULL)return -1;
Int l=update_H(t->left);
Int r=update_H(t->right);
- >height=max(l,r)+1;
Return t->height;
}
Int Height(node* a){
Return a==NULL?-1”a->height;
}
2,旋转操作:
当前子树为root
左边的子树的高度为l1,右边为r1
2.1左边更高
2.1.1 左边的左边发生了插入,让左边提升


我们需要把B提升,A下降然后b右子树变成a的左子树
插入前后我们发现,高度没变
Void LL(node* & A){
Node* B=a->left;
- >left=B->right;
- >right=A;
Update_H(A);
Update_H(B);
A=B;
}
2.1.2左边的右边发生了插入,让左边的右边提升


将C的更低的子树交给B,然后让C提升,然后让C再次提升,将高的子树交给A
void LR(node* &A) {
RR(A->left);
LL(A);
}
2.2.1右边的右边发生了插入


void RR(AVLnode* &A) {
AVLnode *B = A->right;
A->right = B->left;
B->left = A;
UpdateHeight(A);
UpdateHeight(B);
A = B;
}
2.2.2右边的左边发生了插入
先让A的右子树的左子树上提,然后再让右子树上移动
void RL(AVLnode* &A){
LL(A->right);
RR(A);
}
注意;我们在插入节点时我们需要从下面向上去调整
比如:依次插入关键字5, 4, 2, 8, 6, 9
插入2时:
 --->
--->
插入6时:
 --->
--->
再插入一个9:

使平衡:
void ReBalance(AVLnode* &t) {
if(t==NULL) return;
if(Height(t->left) - Height(t->right)==2){ //左边更深
if(Height(t->left->left) >= Height(t->left->right)) //左边的左边更深
LL(t);
else //右边更深
LR(t);
}else if(Height(t->right) - Height(t->left)==2){
if(Height(t->right->right) >= Height(t->right->left))
RR(t);
else
RL(t);
}
Update_H(t); //更新高度
}
插入:
void Insert(AVLnode* &root, int K) {
if(root==NULL) root=new AVLnode(K);
else if(K < root->key) //在左子树插入
Insert(root->left, K);
else if(K > root->key) //在右子树插入
Insert(root->right, K);
ReBalance(root);
}
删除
和二叉树的删除差不多,需要注意的是删除之后的平衡的保持
所以代码是一样的,只是最后需要加一个使平衡
void remove(AVLnode* &root, int K) {
if(root==NULL) return;
if(K<root->key) remove(root->left, K);
//在左子树删K
else if(K>root->key) remove(root->right, K); //在右子树删K
else if(root->left!=NULL && root->right!=NULL){
AVLnode *s=root->right;
while(s->left!=NULL) s=s->left;
root->key=s->key; //s为t右子树中根序列第一个结点
remove(root->right, s->key);
}else{
AVLnode* oldroot=root;
root=(root->left!=NULL)? root->left:root->right;
delete oldroot;
}
ReBalance(root);
}
高度平衡树总结
➢AVL树的高度为O(logn),因此使插入、删除、查找的最坏时间复杂度均为O(logn)。
➢删除操作最坏情况下需要做O(logn)次旋转。
➢对任意连续多次删除操作,每次删除所需的均摊旋转次数为O(1)[1]。对于任意多次插入和删除的混合序列,存在精心构造出的特定操作序列,使每次删除所需的均摊旋转次数为O(logn)
相关文章:

数据结构复习 (二叉查找树,高度平衡树AVL)
1.二叉查找树: 为了更好的实现动态的查找(可以插入/删除),并且不超过logn的时间下达成目的 定义: 二叉查找树(亦称二叉搜索树、二叉排序树)是一棵二叉树,其各结点关键词互异,且中根序列按其关键词递增排列。 等价描述: 二叉查找…...

FreeSWITCH 简单图形化界面39 - Windows安装FreeSWITCH For IPPBX(WSL环境)
FreeSWITCH 简单图形化界面39 - Windows安装FreeSWITCH For IPPBX(WSL环境) 0、界面预览1、部署WSL1.1 安装WSL1.2 安装Windows Terminal1.3 安装WSL配置工具 2、安装Ubuntu24.043、安装FreeSWITCH4、登录Web4.1 80端口占用了 5、测试6、卸载 0、界面预览…...

uniapp - 小程序实现摄像头拍照 + 水印绘制 + 反转摄像头 + 拍之前显示时间+地点 + 图片上传到阿里云服务器
前言 uniapp,碰到新需求,反转摄像头,需要在打卡的时候对上传图片加上水印,拍照前就显示当前时间日期地点,拍摄后在呈现刚才拍摄的图加上水印,最好还需要将图片上传到阿里云。 声明 水印部分代码是借鉴的…...
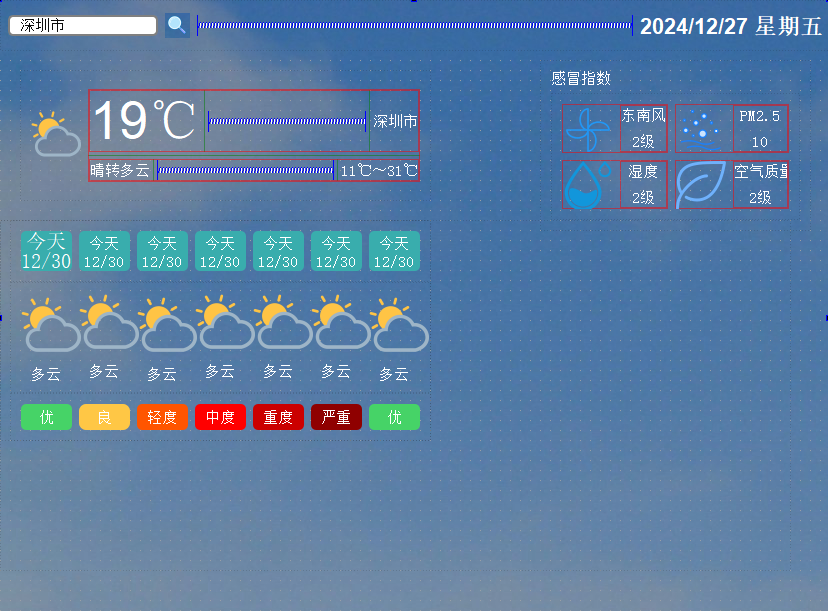
Qt天气预报系统设计界面布局第四部分左边
Qt天气预报系统设计 1、第四部分左边的第一部分1.1添加控件1.2修改控件名字 2、第四部分左边的第二部分2.1添加控件2.2修改控件名字 3、第四部分左边的第三部分3.1添加控件3.2修改控件名字 4、对整个widget04l调整 1、第四部分左边的第一部分 1.1添加控件 拖入一个widget&…...
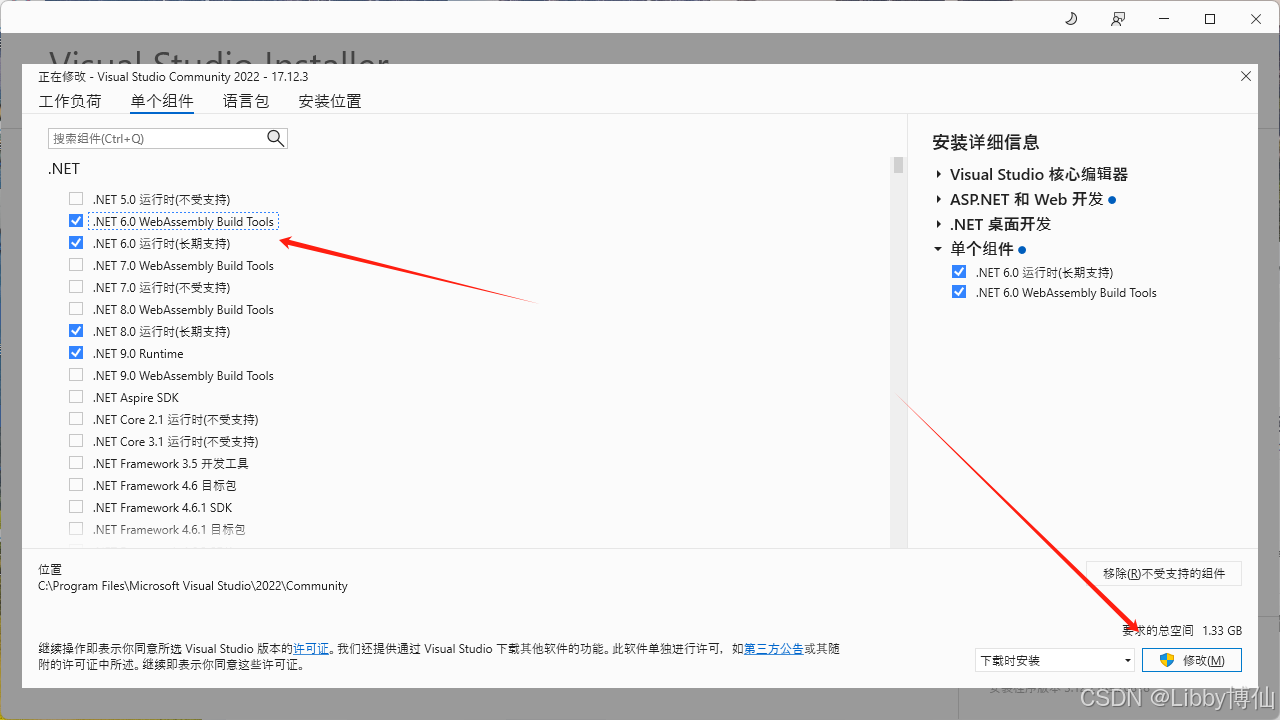
VS无法找到低版本的.net,vs2022创建不了.net6的项目
很多人会遇到安装完vs最新版(目前是2022)之后,创建不了旧版本的.net项目了,比如我在学习.net core 6,我的2022无法创建,只能创建.netcore8的项目,以及又安装了2019,同样无法创建,接下来介绍怎么…...

C++软件设计模式之解释器模式
解释器模式的目的和意图 解释器模式(Interpreter Pattern)是一种行为设计模式,主要用于定义一种语言的文法,并通过该文法解释语言中的句子(表达式)。解释器模式的核心思想是将一个特定的语言表示为其文法规…...
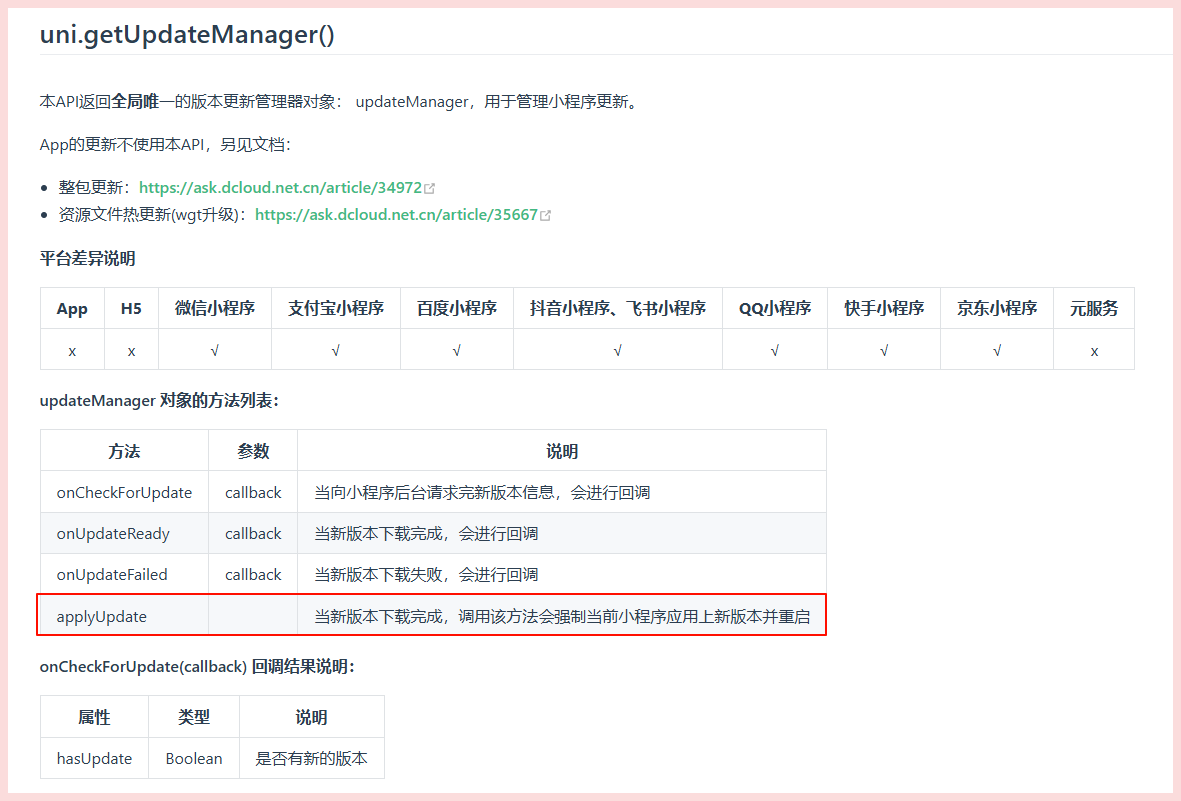
小程序发版后,用户使用时,强制更新为最新版本
为什么要强制更新为最新版本? 在小程序的开发和运营过程中,强制用户更新到最新版本是一项重要的策略,能够有效提升用户体验并保障系统的稳定性与安全性。以下是一些主要原因: 1. 功能兼容 新功能或服务通常需要最新版本的支持&…...
如何使用AI工具cursor(内置ChatGPT 4o+claude-3.5)
⚠️温馨提示: 禁止商业用途,请支持正版,充值使用,尊重知识产权! 免责声明: 1、本教程仅用于学习和研究使用,不得用于商业或非法行为。 2、请遵守Cursor的服务条款以及相关法律法规。 3、本…...

说说缓存使用的具体场景都有哪些?缓存和数据库一致性问题该如何解决?缓存使用常见问题有哪些?
面试官:说说缓存使用的具体场景都有哪些?缓存和数据库一致性问题该如何解决?缓存使用常见问题有哪些? 缓存的具体使用场景有这些: 数据频繁读取: 当某些数据频繁被读取而不常变化时,可以将这些…...
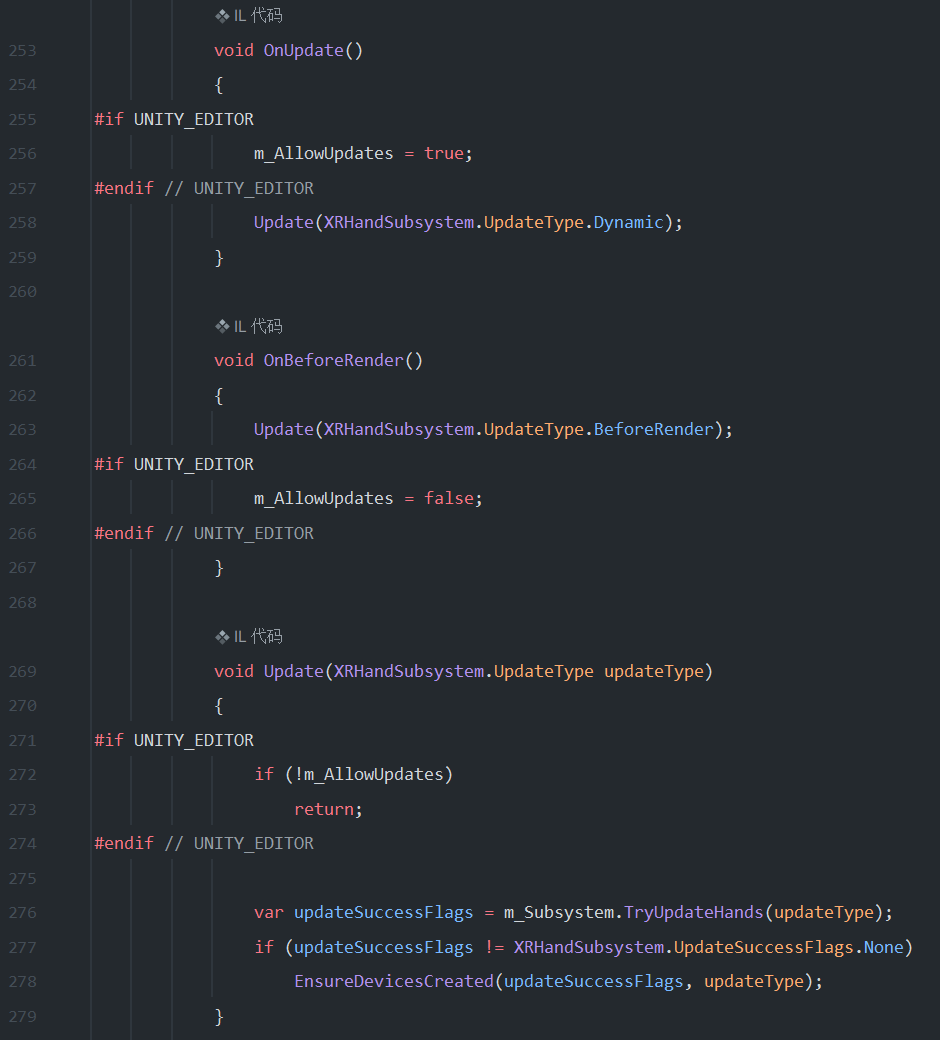
2025-01-01 NO2. XRHands 介绍
文章目录 软件配置1 XR Hands 简介2 XRHand2.1 Pose2.2 Handedness 3 XRHandJoint3.1 XRHandJointID3.2 XRHandJointTrackingState 4 XRHandSubsystem4.1 数据属性4.1.1 UpdateSuccessFlags4.1.2 UpdateType 4.2 处理器管理:注册和注销4.3 更新手部数据:…...
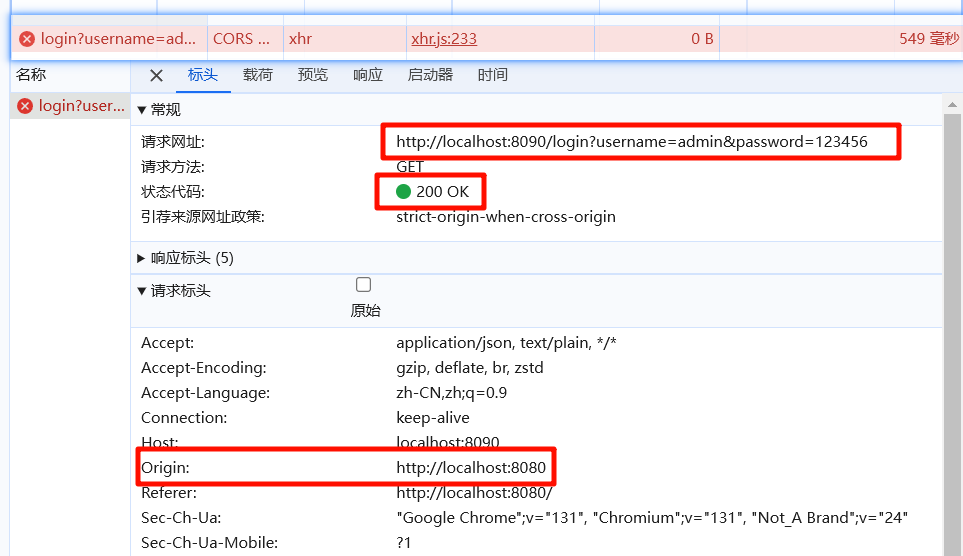
Java开发-后端请求成功,前端显示失败
文章目录 报错解决方案1. 后端未配置跨域支持2. 后端响应的 Content-Type 或 CORS 配置问题3. 前端 request 配置问题4. 浏览器缓存或代理问题5. 后端端口未被正确映射 报错 如下图,后端显示请求成功,前端显示失败 解决方案 1. 后端未配置跨域支持 …...

未来20年在大语言模型相关研究方向--大语言模型的优化与改进
未来20年在大语言模型相关研究方向 模型性能优化 模型架构创新:研究新型的模型架构,如探索更高效的Transformer变体、融合递归神经网络(RNN)和卷积神经网络(CNN)的优点,以提高模型的性能、可扩展性和适应性,满足不同应用场景对模型效率和效果的要求。高效训练算法:开…...

[react] 纯组件优化子
有组件如下,上面变化秒数, 下面是大量计算的子组件,上面每一秒钟变化一次,这时候子组件会不断重新渲染, 浪费资源 父组件如下 import React, { memo, useEffect, useMemo, useState } from react; import type { ReactNode, FC } from react; import HugeCount from ./Te; int…...
美观强大的文件保险库Chibisafe
简介 什么是 Chibisafe ? Chibisafe 是一款用 Typescript 编写的快速文件上传服务,非常实用。它接受文件、照片、文档以及您能想到的任何内容,并返回可共享的链接,供您发送给其他人。它易于使用、易于部署、免费且开源࿰…...
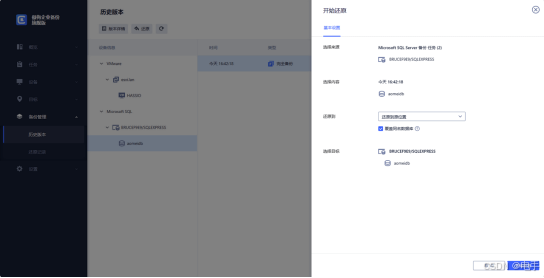
详细教程:SQL2008数据库备份与还原全流程!
数据的安全性至关重要,无论是操作系统、重要文件、磁盘存储,还是企业数据库,备份都是保障其安全和完整性的关键手段。拥有备份意味着即使发生误删、系统崩溃或病毒攻击等问题,也能迅速通过恢复功能解决,避免数据丢失带…...

HTML——49.header和footer标签
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title>header和footer标签</title></head><body><!--header和footer标签:是html5中新标签--><!--header:定义文档的页眉,通常用来定义可见…...
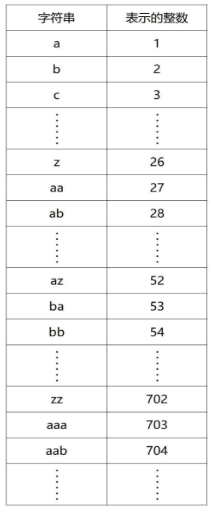
【蓝桥杯选拔赛真题87】python输出字符串 第十五届青少年组蓝桥杯python选拔赛真题 算法思维真题解析
目录 python输出字符串 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 七、 推荐资料 1、蓝桥杯比赛 2、考级资料 3、其它资料 python输出字符串 第十五届蓝桥杯青少年组python比赛选拔赛真题详细解析…...

OpenStack-Dashboard界面简单修改
OpenStack Dashboard界面替换图片 一、dashboard界面Logo的路径及文件 dashboard的Logo存放(在Controller节点)的路径: /usr/share/openstack-dashboard/openstack_dashboard/static/dashboard/img/涉及需要修改的文件(3个&…...
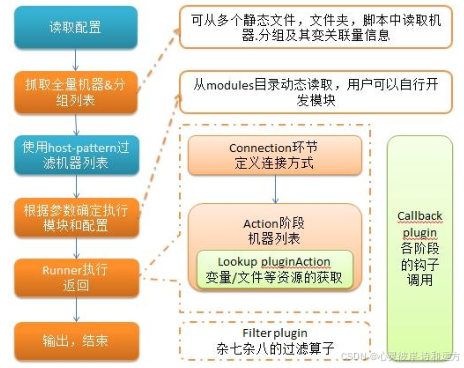
DevOps工程技术价值流:Ansible自动化与Semaphore集成
在DevOps的浪潮中,自动化运维工具扮演着举足轻重的角色。Ansible,作为一款新兴的自动化运维工具,凭借其强大的功能和灵活性,在运维领域迅速崭露头角。本文将深入探讨Ansible的特点、架构、工作原理,以及其应用场景&…...
【服务器】上传文件到服务器并训练深度学习模型下载服务器文件到本地
前言:本文教程为,上传文件到服务器并训练深度学习模型,与下载服务器文件到本地。演示指令输入,完整的上传文件到服务器,并训练模型过程;并演示完整的下载服务器文件到本地的过程。 本文使用的服务器为云服…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
