LeetCode 热题 100_二叉树的直径(40_543_简单_C++)(二叉树;递归)
LeetCode 热题 100_二叉树的直径(40_543)
- 题目描述:
- 输入输出样例:
- 题解:
- 解题思路:
- 思路一(递归):
- 代码实现
- 代码实现(思路一(递归)):
- 以思路一为例进行调试
题目描述:
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
输入输出样例:
示例 1:

输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
提示:
树中节点数目在范围 [1, 104] 内
-100 <= Node.val <= 100
题解:
解题思路:
思路一(递归):
1、我们可以采用和计算二叉树深度同样的思想,计算二叉树的深度是挑选左右子树中深度的最大值,而二叉树的直径是左子树的最大深度深度+右子树的最大深度。
2、复杂度分析:
① 时间复杂度:O(N),其中 N 为二叉树的节点数,即遍历一棵二叉树的时间复杂度,每个结点只被访问一次。
② 空间复杂度:O(h),其中 h 为二叉树的高度(递归需要额外的栈空间)。
本题的力扣官方题解链接(非常不错)
代码实现
代码实现(思路一(递归)):
//二叉树的直径
int diameterOfBinaryTree(TreeNode* root) {depth(root);return ans;
}int depth(TreeNode *root){if(root==nullptr) return 0;//left:左子树的高度(高度指从叶结点开始测量)int left=depth(root->left);//right:右子树的高度int right=depth(root->right);//更新树的最大直径ans=max((left+right),ans);// 返回当前节点的深度return max(left,right)+1;
}
以思路一为例进行调试
#include<iostream>
#include<vector>
#include<queue>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode():val(0),left(nullptr),right(nullptr){}TreeNode(int x):val(x),left(nullptr),right(nullptr){}TreeNode(int x,TreeNode *left,TreeNode *right):val(x),left(left),right(right){}
};class Soluton
{int ans=0;//注意递归返回的是深度,所以我们要分成两个函数int depth(TreeNode *root){if(root==nullptr) return 0;//left:左孩子子树的高度(高度指从叶结点开始测量)int left=depth(root->left);//right:右孩子子树的高度int right=depth(root->right);//求当前两节点间的最大长度ans=max((left+right),ans);return max(left,right)+1;}public://二叉树的直径int diameterOfBinaryTree(TreeNode* root) {depth(root);return ans;}//通过数组创建二叉树(数组元素为-1代表nullptr)TreeNode *creatTree(vector<int> nums){if(nums.empty()) return nullptr;TreeNode *root=new TreeNode(nums[0]);queue<TreeNode *> q;q.push(root);int i=1;while (i<nums.size()){TreeNode *node=q.front();q.pop();if(i<nums.size()&&nums[i]!=-1){node->left=new TreeNode(nums[i]);q.push(node->left);}++i;if(i<nums.size()&&nums[i]!=-1){node->right=new TreeNode(nums[i]);q.push(node->right);}++i;}return root;}//中序遍历输出二叉树(用于调试二叉树创建是否正确)void inorder(TreeNode *root){if(root==nullptr) return ;inorder(root->left);cout<<root->val<<" ";inorder(root->right);}
};int main(){vector<int> nums={1,2,3,4,5};Soluton s;//创建二叉树TreeNode *root=s.creatTree(nums);//调试二叉树是否创建正确//s.inorder(root); cout<<"二叉树的直径:"<<s.diameterOfBinaryTree(root);return 0;
}
LeetCode 热题 100_二叉树的直径(40_543)原题链接
欢迎大家和我沟通交流(✿◠‿◠)
相关文章:

LeetCode 热题 100_二叉树的直径(40_543_简单_C++)(二叉树;递归)
LeetCode 热题 100_二叉树的直径(40_543) 题目描述:输入输出样例:题解:解题思路:思路一(递归): 代码实现代码实现(思路一(递归)&#…...

【数据结构】线性数据结构——链表
1. 定义 链表是一种线性数据结构,由多个节点(Node)组成。每个节点存储数据和指向下一个节点的指针。与数组不同,链表的节点不需要在内存中连续存储。 2. 特点 动态存储: 链表的大小不固定,可以动态增加或…...

开源存储详解-分布式存储与ceph
ceph体系结构 rados:reliable, autonomous, distributed object storage, rados rados采用c开发 对象存储 ceph严格意义讲只提供对象存储能力,ceph的块存储能力实际是基于对象存储库librados的rbd 对象存储特点 对象存储采用put/get/delete…...

[算法] [leetcode-509] 斐波那契数
509 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 n…...

运维人员的Go语言学习路线
以下是一份更为详细的适合运维人员的Go语言学习路线图: 一、基础环境搭建与入门(第 1 - 2 周) 第 1 周 环境搭建 在本地开发机和常用的运维服务器环境(如 Linux 系统)中安装 Go 语言。从官方网站(https://…...

[创业之路-222]:波士顿矩阵与GE矩阵在业务组合选中作用、优缺点比较
目录 一、波士顿矩阵 1、基本原理 2、各象限产品的定义及战略对策 3、应用 4、优点与局限性 二、技术成熟度模型与产品生命周期模型的配对 1、技术成熟度模型 2、产品生命周期模型 3、技术成熟度模型与产品生命周期模型的配对 三、产品生命周期与产品类型的对应关系 …...

安卓入门十一 常用网络协议四
MQTT(Message Queuing Telemetry Transport) MQTT是一种轻量级的、发布/订阅模式的消息传输协议。它被设计用于在低带宽或不稳定网络环境下,实现物联网设备之间的可靠通信。 4.1 MQTT详细介绍 发布/订阅模式:MQTT 使用发布/订…...

《机器学习》——利用OpenCV库中的KNN算法进行图像识别
文章目录 KNN算法介绍下载OpenCV库实验内容实验结果完整代码手写数字传入模型训练 KNN算法介绍 一、KNN算法的基本要素 K值的选择:K值代表选择与新测试样本距离最近的前K个训练样本数,通常K是不大于20的整数。K值的选择对算法结果有重要影响,…...

StarRocks 存算分离在得物的降本增效实践
编者荐语: 得物优化数据引擎布局,近期将 4000 核 ClickHouse 迁移至自建 StarRocks,成本降低 40%,查询耗时减半,集群稳定性显著提升。本文详解迁移实践与成果,文末附丁凯剑老师 StarRocks Summit Asia 2024…...

Tube Qualify弯管测量系统在汽车管路三维检测中的应用
从使用量上来说,汽车行业是使用弯管零件数量最大的单一行业。在汽车的燃油,空调,排气,转向,制动等系统中都少不了管路。汽车管件形状复杂,且由于安装空间限制,汽车管件拥有不同弯曲半径…...

udp分片报文发送和接收
读文件通过udp分片发送的目的端:(包含错误的分片包) #!/usr/bin/python # -*- coding: utf-8 -*-#python send_100frag_file.py -p 55432 -f snatdownloadimport argparse import loggingfrom scapy.all import *# Define the maximum size …...

【从零开始入门unity游戏开发之——C#篇39】C#反射使用——Type 类、Assembly 类、Activator 类操作程序集
文章目录 前言一、前置知识1、编译器2、程序集(Assembly)3、元数据(Metadata) 二、反射1、反射的概念2、反射的作用3、反射的核心Type 类3.1 Type 类介绍3.2 不同方法获取 Type3.3 获取type类型所在的程序集的相关信息 4、反射的常…...

安卓触摸事件的传递
setOnTouchListener()返回值的副作用(触摸事件是否继续往下或往后传递)如下: 返回值效果是否往下层view传递是否往当前view的后续监听传递true该pointer离开屏幕前的后续所有触摸事件都会传递给该TouchListener否否false该pointer离开屏幕前…...
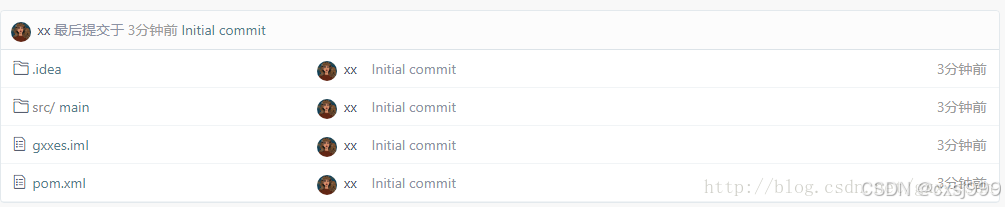
idea项目导入gitee 码云
1、安装gitee插件 IDEA 码云插件已由 gitosc 更名为 gitee。 1 在码云平台帮助文档http://git.mydoc.io/?t153739上介绍的很清楚,推荐前两种方法, 搜索码云插件的时候记得名字是gitee,gitosc已经搜不到了。 2、使用码云托管项目 如果之…...

典型常见的基于知识蒸馏的目标检测方法总结三
来源:Google学术2023-2024的顶会顶刊论文 NeurIPS 2022:Towards Efficient 3D Object Detection with Knowledge Distillation 为3D目标检测提出了一种知识蒸馏的Benchmark范式,包含feature的KD,Logit的cls和reg的KD,…...

端口被占用
端口8080被占用 哈哈哈,我是因为后端项目跑错了,两个项目后端名称太像了; (1)netstat -aon | findstr 8080,找到占用8080端口的进程号,获取对应的进程号pid; (2&#…...
)
Javascript知识框架图(待完善)
以下是一个清晰且详细的 JavaScript 知识框架,涵盖基础知识到高级概念,适合学习和参考: JavaScript 知识框架 1. 基础知识 数据类型 原始类型:Number,String,Boolean,Null,Undefin…...

清华大学Python包镜像站点
清华大学提供了一个Python包镜像站点,其中包括了许多常用的Python包。使用这个镜像站点可以提高下载Python包时的速度,因为包已经存储在国内的服务器上,从而减少了网络延迟。 要使用清华的pip镜像,你可以在pip命令中指定-i参数来…...

逆境清醒文章总目录表
逆境清醒文章总目录表 零、时光宝盒🌻 (https://blog.csdn.net/weixin_69553582 逆境清醒) 《你的答案》歌曲原唱:阿冗,填 词:林晨阳、刘涛,谱曲:刘涛 也许世界就这样,…...

LeetCode算法题——移除元素
题目描述 给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。 假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作࿱…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
