【MATLAB】绘制投资组合的有效前沿
文章目录
- 一、数据准备
- 二、有效前沿
- 三、代码
- 3.1 数据批量读取、预处理
- 3.2 绘制可行集
- 3.3 绘制有效前沿
- 3.4 其它-最大夏普率
一、数据准备
准备多个股票的的历史数据,目的就是找到最优的投资组合。
下载几个标普500里面的公式的股票数据吧,下载方法也可以看我的上一篇文章:【MATLAB】股票(和指数)数据下载–雅虎财经

用你自己的数据也是一样的。
二、有效前沿
有效前沿(Efficient Frontier)是现代投资组合理论中的一个核心概念,最早由经济学家哈里·马科维茨(Harry Markowitz)于1952年提出。
它表示在给定的风险水平下,能够实现的最高预期收益,或者在给定的预期收益下,能够承担的最低风险。
有效前沿不仅是投资组合选择的理论基础,也广泛应用于其他领域,如资源优化、决策分析等。
在投资领域,有效前沿通常通过均值-方差优化模型进行描述。在该模型中,风险由资产收益的标准差(或方差)表示(也称为波动率),收益由资产的预期收益率表示。
有效前沿上的每一个点都代表一个优化的投资组合,它在某个特定风险水平下提供最高的预期回报。
构建有效前沿的基本步骤包括:
-
确定投资资产集合:选择能够构成投资组合的资产。这些资产可以是股票、债券、房地产等。
-
估计资产的预期收益与风险:计算每个资产的预期收益(通常基于历史数据或市场预期)以及各个资产之间的相关性(即协方差矩阵)。
-
计算投资组合的收益与风险:对于不同的资产组合,可以通过加权平均计算组合的预期收益和组合的风险(标准差)。组合的风险不仅依赖于单个资产的风险,还受到各资产之间的相关性影响。
-
优化组合:通过数学优化方法(如线性规划、二次规划等),寻找在不同风险水平下提供最大收益的资产组合。这个过程可以利用均值-方差优化或其他先进算法。
-
绘制有效前沿:根据不同风险水平下优化出的资产组合,绘制收益-风险图,得到有效前沿曲线。
有效前沿可以通过以下数学公式来描述。假设有一个包含 n n n个资产的投资组合,其中每个资产的预期收益为 r i r_i ri,资产的权重为 x i x_i xi,且资产收益的协方差矩阵为 Σ \Sigma Σ,则投资组合的预期收益 R p R_p Rp和风险 σ p \sigma_p σp分别为:
- 投资组合预期收益:
R p = ∑ i = 1 n x i r i R_p = \sum_{i=1}^{n} x_i r_i Rp=i=1∑nxiri
-
投资组合风险(标准差、波动率):
σ p = ∑ i = 1 n ∑ j = 1 n x i x j σ i j \sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} x_i x_j \sigma_{ij}} σp=i=1∑nj=1∑nxixjσij
其中, σ i j \sigma_{ij} σij是资产 i i i和资产 j j j的协方差。
通过调整资产的权重 x i x_i xi,可以得到一系列不同风险水平下的投资组合,最终形成有效前沿。
你可能看到的是下面的公式,它和前面的是一样的: σ p = w T Σ w \sigma_p = \sqrt{\mathbf{w}^T \Sigma \mathbf{w}} σp=wTΣw
其中:
- σ p \sigma_p σp 是投资组合的波动率。
- w \mathbf{w} w 是投资组合的权重向量(例如, w 1 , w 2 , … , w n w_1, w_2, \dots, w_n w1,w2,…,wn,表示每个资产在组合中的比例)。
- Σ \Sigma Σ 是资产收益率的协方差矩阵,描述了不同资产之间的相关性和波动性。
有效前沿的意义与应用:
-
优化投资组合:有效前沿帮助投资者在给定的风险承受能力下,选择最优的资产组合。在风险-收益权衡中,任何位于有效前沿上的投资组合都不能通过改变权重来提高收益而不增加风险。
-
风险管理:通过有效前沿,投资者可以直观地了解在不同风险水平下可获得的最大收益,从而做出更为理性的投资决策。
-
现代投资理论的基石:有效前沿是现代投资组合理论的核心,它推动了金融市场中基于数学优化的投资策略的广泛应用,如资本资产定价模型(CAPM)等。
-
跨领域应用:除了投资领域,有效前沿的思想也应用于多个领域,如供应链管理中的资源分配、生产管理中的成本控制、工程设计中的性能优化等。
尽管有效前沿是一个理论上非常优越的工具,但其也存在一定局限性:
-
依赖历史数据:有效前沿的构建依赖于对历史数据的估计,然而,历史收益并不一定能准确预测未来的表现,尤其是在市场波动剧烈时。
-
假设过于理想化:现代投资组合理论假设资产收益是正态分布的,而实际上,金融市场中的资产收益可能具有偏度和峰度,这使得均值-方差优化在实际应用中可能存在偏差。
-
忽略了投资者的其他需求:有效前沿关注的是收益和风险的权衡,而忽略了投资者的其他需求,如流动性、税务等。
为了克服这些问题,研究人员提出了多种改进方法,例如:
- 引入更多的风险度量指标:如条件风险价值(CVaR)、最坏情况下的风险(worst-case risk)等。
- 使用贝叶斯方法:利用贝叶斯推断来改进参数估计,减少数据不确定性对有效前沿的影响。
- 引入行为金融学的视角:将投资者心理、行为偏差等因素纳入投资决策中,提供更为全面的投资建议。
三、代码
3.1 数据批量读取、预处理
7支股票数据放在一个文件夹里面:

直接读取该文件夹内所有excel文件,已经股票名称。
%% 读取股票数据,放到一个table里面,只要收盘价格% 获取stock目录下所有Excel文件
files = dir('stock/*.xlsx');% 初始化一个空数组,用来存储所有文件的收盘数据
allClosePrices = [];
% 股票名称
stock_name = {};% 循环遍历每个Excel文件
for i = 1:length(files)% 获取当前文件的完整路径filePath = fullfile('stock', files(i).name);% 保存股票名称stock_name = [stock_name,strtok(files(i).name,'_')];% 读取Excel文件中的数据data = readtable(filePath, 'VariableNamingRule', 'preserve');% 检查该文件是否包含 '收盘' 列if ismember('收盘', data.Properties.VariableNames)% 提取 '收盘' 列数据closePrices = data.('收盘');% 将收盘数据合并到 allClosePrices 中allClosePrices = [allClosePrices, closePrices];elsewarning('文件 %s 不包含 "收盘" 列。', files(i).name);end
end% 创建table
stock_data = table(data.("日期"));
stock_data = [stock_data,array2table(allClosePrices)];% 列命名
stock_data.Properties.VariableNames = ['日期',stock_name];结果:

如果你的数据有缺失值,比如某至股票某些交易日数据丢失了,可以选择删除这一天的所有数据,或者用均值填充,用临近的值填充等。
我使用的数据没有缺失值。
%% 数据预处理,缺失值处理% 提取一下价格矩阵
price_data = table2array(stock_data(:,2:8));% 用均值填补缺失值
for i = 1:size(price_data, 2)% 计算该列非缺失值的均值column_mean = nanmean(price_data(:, i));% 找到缺失值的位置并用均值填补price_data(isnan(price_data(:, i)), i) = column_mean;
end% 删除缺失值
% price_data = rmmissing(price_data);3.2 绘制可行集
随机生成2000个权重即投资组合,然后计算收益率、波动率,画出散点图,就做出了投资组合的可行集。

%% 收益率相关计算% 计算每日收益率
daily_returns = diff(log(price_data)); % 求每支股票的年化平均收益率
mean_returns = mean(daily_returns)*252;% 计算收益率的协方差矩阵
cov_matrix = cov(daily_returns)*252;%% 模拟投资组合% 设置模拟的投资组合数目
num_portfolios = 2000;
% 初始化权重矩阵为0矩阵
weights = zeros(num_portfolios, length(stock_name));port_returns = zeros(num_portfolios, 1);
port_volatility = zeros(num_portfolios, 1);
port_sharpe = zeros(num_portfolios, 1);% 随机生成投资组合权重
for i = 1:num_portfolios% 随机权重w = rand(1, length(stock_name));w = w / sum(w); % 使权重总和为1% 计算组合的收益率和波动率portfolio_return = sum(w .* mean_returns);portfolio_volatility = sqrt(w * cov_matrix * w');% 存储结果weights(i, :) = w;port_returns(i) = portfolio_return;port_volatility(i) = portfolio_volatility;% 计算夏普比率,假设无风险利率为2%port_sharpe(i) = (portfolio_return -0.02)/ portfolio_volatility;
end%% 绘制可行集figure;
scatter(port_volatility, port_returns, 10, port_sharpe, 'filled');
title('有效前沿');
xlabel('波动率');
ylabel('收益率');
grid minor
hold on
3.3 绘制有效前沿
matlab的函数是:Portfolio
(旧版的叫啥我忘了,反正推荐用新的就行)
自己去看matlab的帮助文档就行,说的很清楚:

有哪些函数,都写的很清楚:

我的示例:

% 创建 Portfolio 对象
p = Portfolio;% 设置资产回报率数据(均值和协方差矩阵)
p = Portfolio(p, 'assetmean', mean_returns, 'assetcovar',cov_matrix);
% 设置上、下限为 1,表示权重之和为 1
p = Portfolio(p, 'lowerbudget', 1, 'upperbudget', 1);% 设置下限为 0,表示不允许空头,最大收益率为xx
p = Portfolio(p, 'lowerbound', 0,'UpperBound',0.5);plotFrontier(p);
title('可行集和有效前沿');
xlabel('波动率');
ylabel('收益率');
grid minor
hold on
3.4 其它-最大夏普率
夏普比率(Sharpe Ratio) 是衡量投资组合风险调整后收益的指标,通常用来比较不同投资的风险收益表现。夏普比率越高,表示单位风险下的回报越好,投资表现越优秀。
夏普比率的计算公式为:
S = R p − R f σ p S = \frac{R_p - R_f}{\sigma_p} S=σpRp−Rf
其中:
- S S S 是夏普比率
- R p R_p Rp 是投资组合的预期收益率
- R f R_f Rf 是无风险利率(通常使用短期国债收益率或类似的低风险投资的回报率)
- σ p \sigma_p σp 是投资组合的波动率(即标准差,表示投资组合的风险)
解释:
- R p − R f R_p - R_f Rp−Rf:投资组合的超额回报(即投资组合回报减去无风险利率)。这个部分衡量了投资组合的实际收益。
- σ p \sigma_p σp:投资组合的风险(波动率)。它表示收益的波动程度。
夏普比率的应用:
- 较高的夏普比率表示相对于承担的风险,投资组合的回报较高。换句话说,投资者用较少的风险获得较好的回报。
- 较低的夏普比率意味着投资组合的回报相对于风险较低,或者相同风险下的回报较差。
夏普比率的改进:
-
年化夏普比率:如果收益率是日常或月度数据,通常将其年化以便比较:
- 日常数据: S annual = S daily × 252 S_{\text{annual}} = S_{\text{daily}} \times \sqrt{252} Sannual=Sdaily×252(通常一年252个交易日)
- 月度数据: S annual = S monthly × 12 S_{\text{annual}} = S_{\text{monthly}} \times \sqrt{12} Sannual=Smonthly×12
-
针对不同时间频率的无风险利率:无风险利率的选择应与数据的时间频率一致,确保一致性。–
用的函数都是Portfolio对象的函数,自己去看具体说明。
%% 计算最大夏普率% 估计有效投资组合以最大化 Portfolio 对象的夏
普比率
weights = estimateMaxSharpeRatio(p);[risk, ret] = estimatePortMoments(p, weights);plot(risk,ret,'*b');
grid minormax_sharpe_ratio = (ret-0.02)/risk;
fprintf('最大夏普率为:%.4f,对应的波动率为:%.4f, 收益率为:%.4f\n',max_sharpe_ratio,risk,ret);%% 估计有效边界上指定数量的最优投资组合% 普比率是投资组合收益率均值与无风险利率之差除以投资组合收益标准差的比率。% 估计有效边界上指定数量的最优投资组合
pwgt = estimateFrontier(p, 100); % 权重% 估计投资组合收益波动率(标准差)和均值
[prsk, pret] = estimatePortMoments(p, pwgt);% 计算它们的夏普率
sharpe_ratio = (pret-0.02)./prsk;相关文章:

【MATLAB】绘制投资组合的有效前沿
文章目录 一、数据准备二、有效前沿三、代码3.1 数据批量读取、预处理3.2 绘制可行集3.3 绘制有效前沿3.4 其它-最大夏普率 一、数据准备 准备多个股票的的历史数据,目的就是找到最优的投资组合。 下载几个标普500里面的公式的股票数据吧,下载方法也可…...

matlab时频分析库
time frequency gallery...

GBase 8s 数据库备份还原
每一天都是一个新的篇章,等待着你去书写属于自己的故事!!! 一:备份 1.1.下载脚本文件,并上传到数据库服务器上相应目录。 解压后目录为: 说明: dbcomm.sh:导出注释脚本…...

C++模板相关概念汇总
文章目录 一、模板的概念与作用二、函数模板模板的非类型参数调用顺序 三、类模板四、模板的编译模型 一、模板的概念与作用 C模板是一种强大的代码复用机制,它允许程序员编写通用的代码,能够处理不同类型的数据,而无需为每种类型都重复编写…...

MYSQL------sql基础
SQL基础与简介 定义:SQL即结构化查询语言(Structured Query Language),是一种特殊目的的编程语言,用于存取数据以及查询、更新和管理关系数据库系统。作用:可以用于数据库的创建、数据的插入、查询、更新和…...

React Router 用法概览
React Router 用法 React 使得开发者能够轻松地创建交互式的单页应用(SPA),单页应用的一个常见挑战是如何处理页面导航和路由吗,React Router 就是解决这个问题的工具 路由(Router)是 React Router 的核心…...

网络安全之高防IP的实时监控精准防护
高防IP是一种网络安全设备,用于保护网络服务不受到各类攻击的影响,确保业务的持续稳定运行。它通过监控、识别和封锁恶意攻击流量,提供高级别的防护,降低业务被攻击的风险,并提升网络的稳定性和可靠性。 一、实时监控的…...

2024年中国新能源汽车用车发展怎么样 PaperGPT(二)
用车趋势深入分析 接上文,2024年中国新能源汽车用车发展怎么样 PaperGPT(一)-CSDN博客本文将继续深入探讨新能源汽车的用车强度、充电行为以及充电设施的现状。 用车强度 月均行驶里程:2024年纯电车辆月均行驶超过1500公里&…...

LINUXC 时间相关操作
文章目录 时间戳获取本地时间struct tm 结构体高精度的时间struct timeval 结构体相关函数time()localtime()gmtime()gettimeofday()strftime()mktime() 示例代码 时间戳 时间戳是指计算机中存储的数字型时间。它是以一个特定的时间点作为起点(通常是1970年1月1日0…...

网络游戏之害
网络游戏之害: 网络游戏于今之世风靡四方,其娱人耳目、畅人心怀之效,固为人知,然所藏之害,若隐伏之暗潮,汹涌而至时,足以覆舟,尤以青年为甚,今且缕析其害,以…...

SpringMVC的消息转换器
SpringMVC的消息转换器(Message Converter)是Spring框架中用于处理HTTP请求和响应体与Java对象之间转换的组件。它们使得开发人员可以轻松地将HTTP请求的数据映射到方法参数,并将返回的对象转换为HTTP响应。 工作原理 当一个HTTP请求到达Spr…...
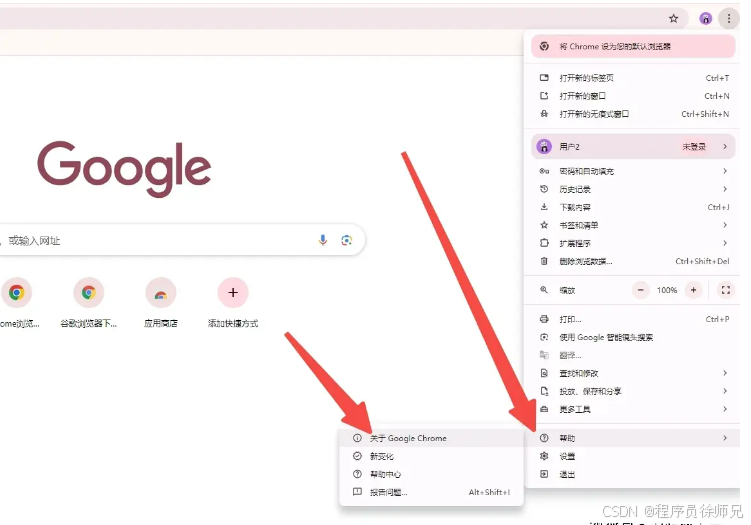
Chrome 浏览器下载安装教程,保姆级教程
大家好,今天我们来聊一聊如何在国内下载和安装最新版本的 Chrome 浏览器。由于众所周知的原因,Google 的网站在国内是被屏蔽的,因此很多朋友在下载 Chrome 浏览器 时会遇到困难。其实,不必担心,今天我将为大家带来一份…...
)
ElasticSearch系列(一)
一.了解ES、倒排索引、es的一些概念、安装es、kibana 二.DSL;索引库操作 三.Java RestClient:索引库操作 一、了解ES、倒排索引、es的一些概念、安装es、kibana kibana、logstash、beats Elasticserach 存储,计算 ,搜索数据 –…...

C++技巧:map和vector
一,map是有序的,unordered_map是无序的 在C中,std::map 和 std::unordered_map 是两种不同的容器,它们都用于存储键值对,但是它们的底层实现和性能特性有所不同。以下是它们的详细介绍: std::map std::m…...

中建海龙:科技助力福城南产业片区绿色建筑发展
在快速发展的城市化进程中,绿色建筑以其环保、节能、可持续的特点日益受到重视。作为建筑工业化领域的领军企业,中建海龙科技有限公司(简称“中建海龙”)凭借其卓越的科技实力和创新举措,在推动绿色建筑发展方面做出了…...

模块化通讯管理机在物联网系统中的应用
安科瑞刘鸿鹏 摘要 随着能源结构转型和智能化电网的推进,电力物联网逐渐成为智能电网的重要组成部分。本文以安科瑞ANet系列智能通信管理机为例,探讨其在电力物联网中的应用,包括数据采集、规约转换、边缘计算、远程控制等技术实践&#…...

建立一个Macos载入image的实例含界面
前言 为了方便ios程序的开发,有时候需要先用的Macos平台进行一些功能性的程序开发。 作为对比和参考。 1、创建一个MacOS的App 2、主界面控件的增加 添加的控件方法与ios相同,也是再用commandshiftL(CtrlShiftL),就会弹出控件…...

Redis List列表
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 Redis List列表 收录于专栏[redis] 本专栏旨在分享学习Redis的一点学习笔记,欢迎大家在评论区交流讨论💌 目录 概述 常用命令 LPUSH …...

继承与多态 - 继承机制、虚函数、纯虚函数
引言 C 是一种支持面向对象编程(OOP)的编程语言,继承和多态是 OOP 的两个核心概念。通过继承,我们可以创建新的类,这些新类可以重用现有类的代码,并且可以根据需要进行扩展或修改。多态则允许我们编写更加…...

【QT】C++线程安全的单例模板
模板代码 #pragma once #include <mutex> #include <atomic>// CRTP基类模板 Curiously Recurring Template Parttern—奇异递归模板模式。 template <typename T> class SingletonCRTP { public:// 禁止拷贝构造和赋值操作SingletonCRTP(const SingletonCR…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
