《深入浅出HTTPS》读书笔记(24):椭圆曲线密码学
《深入浅出HTTPS》读书笔记(24):椭圆曲线密码学
为了保证DH的密钥对不被破解,提升安全性的主要手段就是增加密钥对的长度,但是长度越长,性能越低。
为了解决性能问题,需要了解下椭圆曲线密码学(Elliptic Curve Cryptography),简称为ECC。
ECC是新一代的公开密钥算法,主要的优点就是安全性,极短的密钥能够提供很大的安全性。
ECC算法的优势就是性能和安全性非常高。
【ECC算法的基本模型】
ECC是比离散对数类算法(比如RSA和DH算法)更复杂的算法。ECC椭圆曲线由很多点组成,这些点由特定的方程式组成的。
椭圆曲线有个特点,任意两个点能够得到这条椭圆曲线上的另外一点,这个操作称为打点,经过多次(比如n次)打点后,能够生成一个最终点(F)。
ECC密码学的关键点就在于就算知道具体方程式、基点(G)、最终点(F),也无法知晓一共打点了多少次(n),这就是椭圆曲线的关键,很难破解打点过程。
椭圆曲线的关键点就是方程式。
必须把所有的操作数限制在一个有限域中,为了控制在有限域中,需要一个很大的质数(p),而这个曲线上的点都必须小于这个质数。
ECC由方程式、基点(G)、质数(P)组成,当然还有a、b这样的方程式参数。
为了安全,系统预先定义了一系列的曲线,称为命名曲线(name curve),比如secp256k1就是一个命名曲线。
相关文章:
:椭圆曲线密码学)
《深入浅出HTTPS》读书笔记(24):椭圆曲线密码学
《深入浅出HTTPS》读书笔记(24):椭圆曲线密码学 为了保证DH的密钥对不被破解,提升安全性的主要手段就是增加密钥对的长度,但是长度越长,性能越低。 为了解决性能问题,需要…...

现代光学基础5
总结自老师的讲义 yt5 开卷考试复习资料:光探测器与光伏技术 目录 光探测器(Photodetector) 工作原理二极管电路连接方式响应度(Responsivity)微弱光检测超导纳米线单光子探测光电二极管噪声 太阳能电池࿰…...

力扣hot100——贪心
121. 买卖股票的最佳时机 class Solution { public:int maxProfit(vector<int>& a) {if (a.size() 1) return 0;int ans 0;int mi a[0];for (int i 1; i < a.size(); i) {ans max(ans, a[i] - mi);mi min(mi, a[i]);}return ans;} };55. 跳跃游戏 class S…...

vue3如何实现防抖?
第一 防抖就是我们设置一个调用时间,点击后设置时间开始倒计时,如果再次点击会重新倒计时 npm或yarn安装: npm install lodash <template><div click"debouncedInputHandler"><button>打印</button>…...
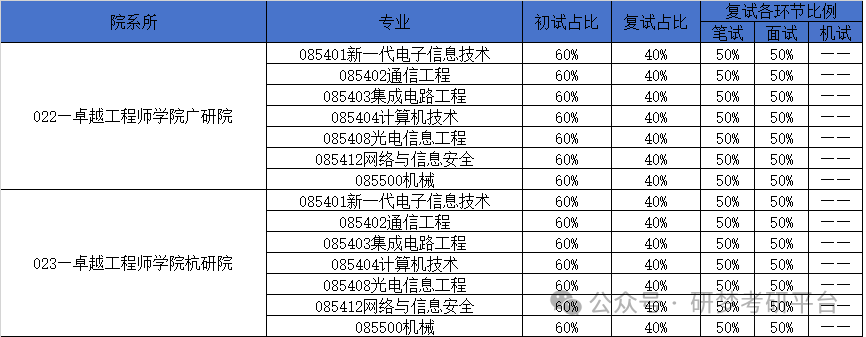
西安电子科技大学初/复试笔试、面试、机试成绩占比
西安电子科技大学初/复试笔试、面试、机试成绩占比 01通信工程学院 02电子工程学院 03计算机科学与技术学院 04机电工程学院 06经济与管理学院 07数学与统计学院 08人文学院 09外国语学院 12生命科学与技术学院 13空间科学与技术学院 14先进材料与纳米科技学院 15网络与信息安…...

spring mvc源码学习笔记之六
pom.xml 内容如下 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...

树莓派4b如何连接ov7670摄像头
在树莓派4B上连接和使用OV7670摄像头是一项具有一定技术挑战的任务。这是因为OV7670摄像头是一个原始的CMOS摄像头模块,它通过并行接口与主机通信,而树莓派的GPIO接口通常用于串行接口(如I2C、SPI、UART)通信,不直接支持并行摄像头接口。因此,需要一些额外的硬件和软件工…...
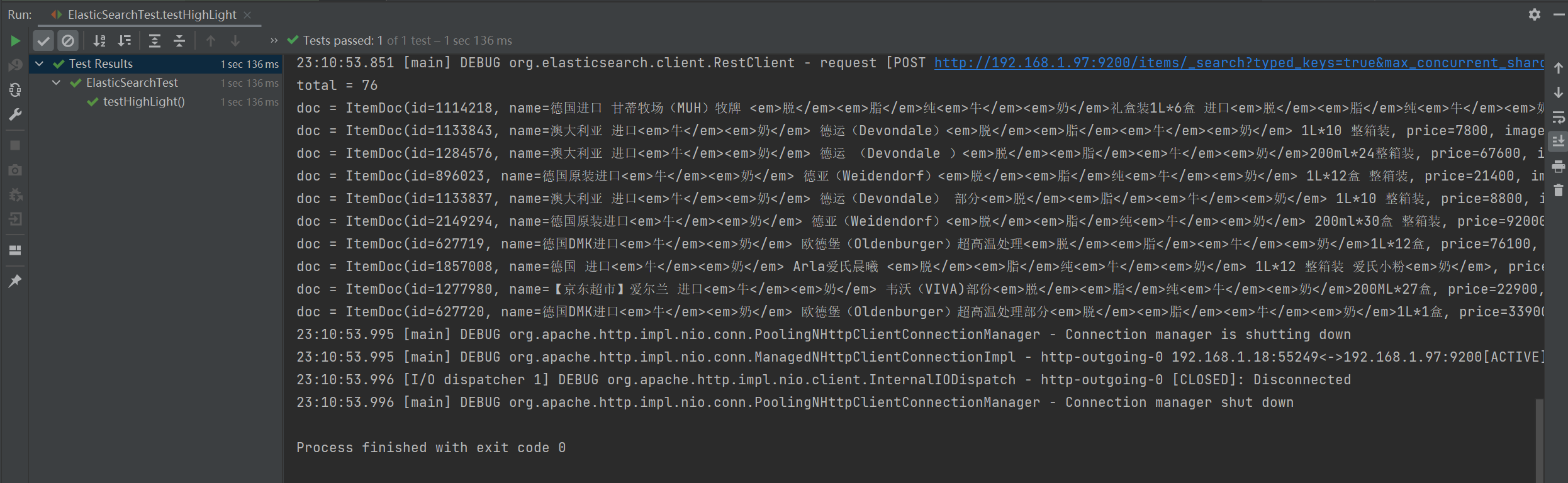
[微服务]分布式搜索Java客户端
快速入门 使用RestClient客户端进行数据搜索可以分为两步 构建并发起请求 代码解读: 第一步,创建SearchRequest对象,指定索引库名第二步,利用request.source()构建DSL,DSL中可以包含查询、分页、排序、高亮等 query…...

如何使用 `uiautomator2` 控制 Android 设备并模拟应用操作_VIVO手机
在 Android 自动化测试中,uiautomator2 是一个非常强大的工具,能够帮助我们通过 Python 控制 Android 设备执行各种操作。今天,我将通过一个简单的示例,介绍如何使用 uiautomator2 控制 Android 设备,执行特定的应用启动、广告跳过以及其他 UI 操作。此示例的目标是自动化…...
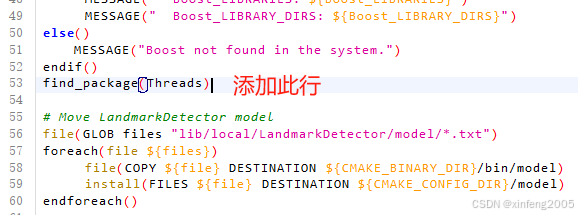
在Ubuntu 18.04.6 LTS安装OpenFace流程
一、修改配置:将gcc8,g8作为默认选项 sudo update-alternatives --install /usr/bin/gcc gcc /usr/bin/gcc-8 100 sudo update-alternatives --config gcc 选择版本,再查看gcc --version sudo update-alternatives --install /usr/bin/g g /usr/bin/g-…...

C 语言的整型提升问题
目录 引言 一、什么是整型提升 二、为什么会有整型提升 三、整型提升的规则 四、整型提升的影响 五、如何避免整型提升带来的问题 六、总结 引言 在 C 语言中,整型提升(Integer Promotion)是一个常常被忽视但却非常重要的概念。理解整…...

第0章 机器人及自动驾驶SLAM定位方法全解析及入门进阶学习建议
嗨,各位同学大家好!笔者自985硕士毕业后,在机器人算法领域已经深耕 7 年多啦。这段时间里,我积累了不少宝贵经验。本专栏《机器人工程师带你从零入门SLAM》将结合下面的SLAM知识体系思维导图及多年的工作实战总结,将逐…...
video.js视频播放上手
html案例 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>videojs视频播放</title> </head> <link href"https://cdnjs.cloudflare.com/ajax/libs/video.js/7.3.0/video-js.min.cs…...

【LLM-Agent】Building effective agents和典型workflows
note Anthropic的工程经验: 大道至简,尽量维护系统的简洁;尽量让过程更加透明(因为你依赖的是LLM的决策,如果只看输出不看过程,很容易陷入难以debug的情况);对LLM需要调用的工具&am…...

《量子比特大阅兵:不同类型量子比特在人工智能领域的优劣势剖析》
在科技的前沿,量子比特与人工智能的融合正开启一扇全新的大门。不同类型的量子比特,如超导、离子阱、光量子等,在与人工智能结合时展现出独特的优势与劣势。 超导量子比特 超导量子比特是目前应用较为广泛且研究相对成熟的量子比特类型。它…...

《探秘开源大模型:AI 世界的“超级引擎”》
《探秘开源大模型:AI 世界的“超级引擎”》 一、开源大模型崛起之路二、开源大模型发展历程回顾(一)早期奠基:理论突破与初步实践(二)快速发展:百花齐放的模型格局(三)当下态势:走向成熟与多元融合三、开源大模型核心技术剖析(一)Transformer 架构:基石之稳(二)…...

el-table行列转换简单版,仅限单行数据
原始数据格式如下,如果不是此格式,请转换成以下格式在进行以下操作 [{ label: name, value: Tom },{ label: age, value: 25 },{ label: country, value: UK } ]代码如下 <template><el-table :data"tableData" style"width: …...

2025年1月4日蜻蜓q旗舰版st完整开源·包含前后端所有源文件·开源可商用可二开·优雅草科技·优雅草kir|优雅草星星|优雅草银满|优雅草undefined
2025年1月4日蜻蜓q旗舰版st完整开源包含前后端所有源文件开源可商用可二开优雅草科技优雅草kir|优雅草星星|优雅草银满|优雅草undefined 产品介绍: 本产品主要贡献者优雅草科技优雅草kir|优雅草星星|优雅草银满|优雅草undefined-青史留名,时光如川浪淘…...

SQL把字符串按逗号分割成记录
在 SQL 中,可以通过以下方法将字符串按逗号分割,并将每个分割的值作为单独的记录插入到结果集中。以下是针对不同数据库系统的实现方法: 1. 使用 STRING_SPLIT(SQL Server 2016) STRING_SPLIT 是 SQL Server 提供的内置…...
:观察者模式)
C#设计模式(行为型模式):观察者模式
C#设计模式:观察者模式,让对象间通信更优雅 在软件开发中,我们经常会遇到一个对象的状态发生改变,其他对象需要自动更新或做出相应反应的场景。例如: GUI事件处理: 当用户点击按钮时,按钮需要…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
