Understanding the Lomb–Scargle Periodogram
- 本文目的:了解Lomb–Scargle Periodogram的原理 (用来估算不均匀采样数据的周期)
- 参考文献Understanding the Lomb–Scargle Periodogram思路:
连续傅里叶变换 --> 离散傅里叶变换(均匀采样–> Classifical periodogram (即Schuster periodogram,均匀采样) --> Lomb–Scargle Periodogram 变换(非均匀采样)
1. Introduction
- 最小平方频谱分析法
-
最小平方频谱分析法(英语:Least-squares spectral analysis)是一种利用最小平方法寻找适配于资料点之最佳正弦曲线,以估算频谱的方法。
-
其数学原理与科学界中最常用的傅立叶分析相似[1][2]。一般而言,傅立叶分析会将间隔较长之讯号的长周期噪声放大,而最小平方频谱分析法则解决了这个问题[3]。
-
最小平方频谱分析法也称为凡尼切克法(Vaníček method)[4]、隆布法(Lomb method)[3][5]或隆布—史卡构法(Lomb–Scargle method)[2][6][7],分别取名自对其有所贡献的佩特·凡尼切克、尼可拉斯·隆布(Nicholas R. Lomb)[8]以及杰佛瑞·史卡构(Jeffrey D. Scargle)[9]。此外,麦可·科恩伯格(Michael Korenberg)、史考特·陈(Scott Chen)以及大卫·多诺霍等人也曾开发出与之关系密切的其它方法。
- Lomb–Scargle method
- 目的:估算不均匀采样数据的周期
- time and phase ?? 时间和相位
2. Background: The continuous Fourier Transform
- 傅里叶对(Fourier pair)
-
傅里叶对(Fourier pair)是指在傅里叶变换中,一组时间域信号与其对应的频率域信号之间的关系。傅里叶变换提供了一种将信号从时间域转换到频率域的方法,使我们能够分析信号的频率成分
-
More quantitatively, (a function with a characteristic scale T) will in general have (a Fourier transform with a characteristic scale of 1/T.)

- 功率谱密度(Power Spectral Density,PSD)
-
功率谱密度(Power Spectral Density,PSD),也会简写为power sectrum。 是描述信号在频域中分布的一个重要概念。它表示单位频率范围内信号的功率。具体来说,PSD提供了信号在不同频率上的功率分布情况,常用于分析信号的频率特性。
-
作用: quantify the contribtuion of each frequency
-
主要特点
单位:PSD的单位通常是功率单位(如瓦特)与频率单位(如赫兹)的比值,例如瓦特/赫兹(W/Hz)。
计算方式:
对于离散信号,PSD可以通过傅里叶变换得到。
常见的计算方法包括使用Welch方法、周期图法等。

- The Convolution Theorem
- 卷积用途:卷积可以看作是将一个函数 "滑过 "另一个函数的操作,每一步都对乘积进行积分。这种操作通常用于平滑函数。

-
傅里叶变换中的卷积定理(Convolution Theorem)是信号处理和系统分析中的一个重要理论。它描述了在时域中进行卷积运算与在频域中进行乘法运算之间的关系。
-
卷积运算在时域中是一个复杂的积分运算,而在频域中则变成了简单的乘法运算。这意味着,如果我们能够计算信号的傅里叶变换,我们就可以通过简单的乘法来求解它们的卷积,从而大大简化计算过程。


3. Window Functions: From Idealized to Real-world Signals
3.1. Effect of a Rectangular Window
- 由于窗口宽度与其变换宽度之间存在反比关系(More quantitatively, a function with a characteristic scale T will in general have a Fourier transform with a characteristic scale of 1/T. ),因此,观测窗口越宽,观测到的傅立叶变换每个峰值的扩散就越小。

3.2. The Dirac Comb and the Discrete Fourier Transform
- 在信号处理的背景下,当一个连续信号以几乎瞬时的方式在固定间隔进行采样时,所使用的窗口函数通常被称为狄拉克梳(Dirac comb)。这一过程可以被视为真实信号与一个狄拉克梳进行逐点乘积,从而实现采样。


3.2.1. The Nyquist Limit
This implies that if we have a regularly sampled function with a sampling rate of f0 = 1/T, we can only fully recover the frequency information if the signal is band limited between frequencies ±f0/2. This is one way to motivate the famous Nyquist sampling limit, which approaches the question from the other direction and states that to fully represent the frequency content of a “band-limited signal” whose Fourier transform is zero outside the range ±B, we must sample the data with a rate of at least fNy = 2B

3.2.2. The Discrete Fourier Transform
- 为什么从连续到离散?When a continuous function is sampled at regular intervals, the delta functions in the Dirac comb window serve to collapse the Fourier integral into a Fourier sum, and in this manner we can arrive at the common form of the discrete Fourier transform.
这里的离散主要指window是连续还是离散的?

3.3. The Classical Periodogram

4. Nonuniform Sampling

(1)傅立叶峰值的位置和高度与观测间隔有关,因此观测时间的随机化会导致傅立叶峰值位置和高度的随机化 (换句话说,非结构化的观测间隔会直接导致窗口变换中出现非结构化的频率峰)。 这种非结构化窗口变换与真实信号的傅立叶变换相卷积后,就会产生反映相同随机噪声的观测傅立叶变换。
Figure 9: Randomization of observation times (left panel,second row不同的间隔T) leads to Randomization of Fourier peak locations and heights s (left panel,final row)

(2)Sampling the signal more densely might alleviate these problems
Figure 10: 提高Randomization of observation times (left panel,second row不同的间隔T) leads to higher performance (left panel,final row不同的间隔T)

4.1.1. Incorrect Limits in the Literature
4.1.2. The Nonuniform Nyquist Limit
4.1.3. Frequency Limit due to Windowing
- 视窗极限 1/(2δt) 与奈奎斯特极限截然不同:奈奎斯特极限是指所有信号都被混叠到奈奎斯特范围内的频率;视窗极限是指所有信号都被衰减为零的频率。
4.2. Semistructured Observing Windows
- Two typical window functions derived from real-world observations: one ground-based (LINEAR) and one space-based (Kepler)


5. From Classical to Lomb–Scargle Periodograms
1. 不同点
-
uniform data: 均匀采样是指在固定的时间间隔或空间分布中,以相同的间隔获取样本数据
-
nonunifrom data: 非均匀采样是指在不规则的时间间隔或空间分布中进行样本数据获取。采样点之间的时间间隔可能是不相等的,通常由于外部因素(如天气变化、设备限制等)导致。
-
Classical Periodogram (Schuster periodogram): uniform data
-
Lomb–Scargle Periodograms: nonunifrom data


2. 相同点

6. The Least-squares Periodogram and Its Extensions
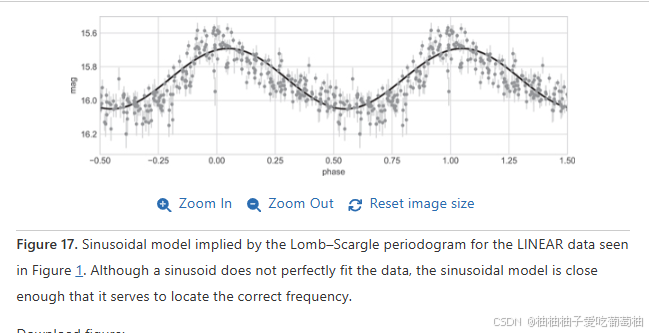
7. Practical Considerations When Using Lomb–Scargle Periodograms
7.1. Choosing a Frequency Grid
-
There are two important considerations: the frequency limits and the grid spacing.
-
More quantitatively, (a function with a characteristic scale T) will in general have (a Fourier transform with a characteristic scale of 1/T.)




Reference
[1] VanderPlas J T. Understanding the lomb–scargle periodogram[J]. The Astrophysical Journal Supplement Series, 2018, 236(1): 16.
相关文章:

Understanding the Lomb–Scargle Periodogram
本文目的:了解Lomb–Scargle Periodogram的原理 (用来估算不均匀采样数据的周期)参考文献Understanding the Lomb–Scargle Periodogram思路: 连续傅里叶变换 --> 离散傅里叶变换(均匀采样–> Classifical perio…...

解决Linux切换用户后的命令提示符为-bashxx$的问题
1、问题描述 切换用户时,命令提示符为-bashxx$ 比如: [rootlocalhost ~]# su zhouxingchi bash-4.2$ ### 显示看着不正常的命令提示符 2、PS1变量 PS1变量就是我们的命令提示符的内容,当我们登录时会加载该变量,从而显示提…...
)
AMP 混合精度训练中的动态缩放机制: grad_scaler.py函数解析( torch._amp_update_scale_)
AMP 混合精度训练中的动态缩放机制 在深度学习中,混合精度训练(AMP, Automatic Mixed Precision)是一种常用的技术,它利用半精度浮点(FP16)计算来加速训练,同时使用单精度浮点(FP32…...
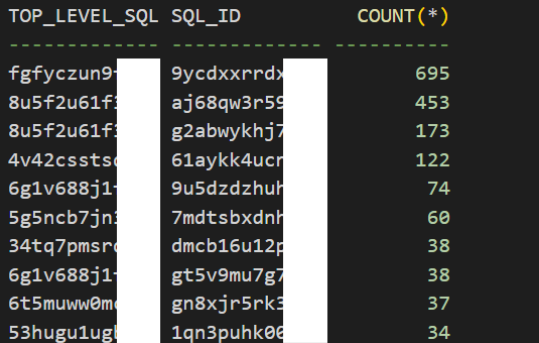
Oracle数据库如何找到 Top Hard Parsing SQL 语句?
有一个数据库应用程序存在过多的解析问题,因此需要找到产生大量硬解析的主要语句。 什么是硬解析 Oracle数据库中的硬解析(Hard Parse)是指在执行SQL语句时,数据库需要重新解析该SQL语句,并创建新的执行计划的过程。这…...

Mono里运行C#脚本25—mono_codegen
前面分析怎么样找到主函数Main的入口点功能,也就是说已经找到了这个函数的CIL代码。虽然找到了代码,但是还不能执行它的,因为它是一种虚拟机的代码。也就是说它是假的代码,不是现实世界存在的机器的代码,因此不能直接执行,必须经过后端编译器的再次编译才能真正运行它。下…...

flink cdc oceanbase(binlog模式)
接上文:一文说清flink从编码到部署上线 环境:①操作系统:阿里龙蜥 7.9(平替CentOS7.9);②CPU:x86;③用户:root。 预研初衷:现在很多项目有国产化的要求&#…...

【WPF】 数据绑定机制之INotifyPropertyChanged
INotifyPropertyChanged 是 WPF 中的一个接口,用于实现 数据绑定 中的 属性更改通知。它的主要作用是,当对象的某个属性值发生更改时,通知绑定到该属性的 UI 控件更新其显示内容。 以下是有关 INotifyPropertyChanged 的详细信息和实现方法&…...
为例及实战应用)
机器学习算法深度解析:以支持向量机(SVM)为例及实战应用
机器学习算法深度解析:以支持向量机(SVM)为例及实战应用 在当今数据驱动的时代,机器学习作为人工智能的一个核心分支,正以前所未有的速度改变着我们的生活与工作方式。从金融风控到医疗诊断,从自动驾驶到智…...

网络编程基础:连接Java的秘密网络
1 网络编程的重要性 网络编程允许Java应用程序与其他计算机或设备进行通信。这包括从简单的数据传输到复杂的分布式系统和Web服务。 2 Java网络编程的核心类 Java提供了多个类来支持网络编程: InetAddress:表示网络上的IP地址。 URL:表示统…...

无监督学习:自编码器(AutoEncoder)
自编码器:数据的净化之旅 引言 自编码器作为一种强大的特征学习方法,已经经历了从简单到复杂的发展历程。本文综述了多种类型的自编码器及其演进过程,强调了它们在数据降维、图像处理、噪声去除及生成模型等方面的关键作用。随着技术的进步…...

在不到 5 分钟的时间内将威胁情报 PDF 添加为 AI 助手的自定义知识
作者:来自 Elastic jamesspi 安全运营团队通常会维护威胁情报报告的存储库,这些报告包含由报告提供商生成的大量知识。然而,挑战在于,这些报告的内容通常以 PDF 格式存在,使得在处理安全事件或调查时难以检索和引用相关…...

Memcached prepend 命令
Memcached prepend 命令用于向已存在 key(键) 的 value(数据值) 前面追加数据 。 语法: prepend 命令的基本语法格式如下: prepend key flags exptime bytes [noreply] value参数说明如下: key:键值 key-value 结构中的 key&a…...

Win10 VScode配置远程Linux开发环境
Windows VScode配置远程Linux开发环境 记录一下在Windows下VScode配置远程连接Linux环境进行开发的过程。 VScode的远程编程与调试的插件Remote Development,使用这个插件可以在很多情况下代替vim直接远程修改与调试服务器上的代码,搭配上VScode的语言…...

微信小程序校园自助点餐系统实战:从设计到实现
随着移动互联网的发展,越来越多的校园场景开始智能化、自助化。微信小程序凭借其轻量化、便捷性和强大的生态支持,成为了各类校园应用的首选工具之一。今天,我们将通过实际开发一个微信小程序“校园自助点餐系统”来展示如何设计和实现这样一…...

解决sublime编译无法输入问题
在使用sublime编译简单的c语言的时候,发现编译过程中,带有scanf的程序,无法正确的输入。 需要提前配置好gcc 和g++ 一、新增配置 新建编译系统文件:C.sublime-build 具体步骤:菜单中选择Tools——Build System——New Build System——保存文件名C.sublime-build ,填写以…...

const修饰指针总结
作者简介: 一个平凡而乐于分享的小比特,中南民族大学通信工程专业研究生在读,研究方向无线联邦学习 擅长领域:驱动开发,嵌入式软件开发,BSP开发 作者主页:一个平凡而乐于分享的小比特的个人主页…...

uniapp实现后端数据i18n国际化
1.在main.js配置请求获取到数据再设置到i18n中, 我这里是通过后端接口先获取到一个多个数据的的json链接,通过链接再获取数据,拿到数据后通过遍历的方式设置i18n //接口数据示例:{"vi": "http://localhost:8899/…...

什么是国密设计
国密设计,全称为“国家密码算法设计”,是指中国自主研发的一系列密码学算法和相关的技术标准。这些算法旨在提供安全可靠的加密、解密、签名验证等服务,并且在中国的信息安全领域中扮演着至关重要的角色。以下是关于国密设计的详细解释&#…...

Android IO 问题:java.io.IOException Operation not permitted
问题描述与处理策略 1、问题描述 java.io.IOException: Operation not permittedjava.nio.file.FileSystemException: /storage/emulated/0/test/test.txt: Operation not permittedjava.io.IOException: Operation not permitted:异常为操作不被允许 java.nio.f…...

安装bert_embedding遇到问题
在使用命令: pip install bert-embedding 安装bert_embedding的时候,遇到如下问题: ERROR: Failed cleaning build dir for numpy Successfully built gluonnlp Failed to build numpy ERROR: ERROR: Failed to build installable wheel…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

CppCon 2015 学习:Simple, Extensible Pattern Matching in C++14
什么是 Pattern Matching(模式匹配) ❝ 模式匹配就是一种“描述式”的写法,不需要你手动判断、提取数据,而是直接描述你希望的数据结构是什么样子,系统自动判断并提取。❞ 你给的定义拆解: ✴ Instead of …...
