android 外挂modem模块实现Telephony相关功能(上网,发短信,打电话)
一.背景
当前模块不支持Telephony相关的功能,例如上网、发短信等功能,就需要外挂另一个模块实现此功能,这就是外挂modem模块实现Telephony功能,此篇主要就是说实现外挂modem模块功能中的Framework层实现逻辑,如下流程是在Android 13中实现的外挂pcie模块的流程
二.ril库相关替换
需要替换libril.so和libreference-ril.so包

三.代码实现流程
1.Android Framework层实现逻辑
UI界面
首先是UI界面将SIM卡以及短信相关界面放出来,如下:
--- a/QSSI.13/packages/apps/Settings/res/xml/network_provider_internet.xml
+++ b/QSSI.13/packages/apps/Settings/res/xml/network_provider_internet.xml
@@ -31,17 +31,6 @@settings:keyw相关文章:

android 外挂modem模块实现Telephony相关功能(上网,发短信,打电话)
一.背景 当前模块不支持Telephony相关的功能,例如上网、发短信等功能,就需要外挂另一个模块实现此功能,这就是外挂modem模块实现Telephony功能,此篇主要就是说实现外挂modem模块功能中的Framework层实现逻辑,如下流程是在Android 13中实现的外挂pcie模块的流程 二.ril库相…...

【计算机视觉技术 - 人脸生成】2.GAN网络的构建和训练
GAN 是一种常用的优秀的图像生成模型。我们使用了支持条件生成的 cGAN。下面介绍简单 cGAN 模型的构建以及训练过程。 2.1 在 model 文件夹中新建 nets.py 文件 import torch import torch.nn as nn# 生成器类 class Generator(nn.Module):def __init__(self, nz100, nc3, n…...

数据中台与数据治理服务方案[50页PPT]
本文概述了数据中台与数据治理服务方案的核心要点。数据中台作为政务服务数据化的核心,通过整合各部门业务系统数据,进行建模与加工,以新数据驱动政府管理效率提升与政务服务能力增强。数据治理则聚焦于解决整体架构问题,确保数据…...

【Qt】将控件均匀分布到圆环上
1. 关键代码 for(int i0; i<10; i){/*m_panLabelIcon - 大圆环控件m_slotsIcon[i] - 小圆控件*/QString idxStr QString::number(i1);m_slotsIcon[i] new QLabel(m_panLabelIcon);m_slotsIcon[i]->setFont(ftSlot);m_slotsIcon[i]->setText(idxStr);m_slotsIcon[i]-…...
)
第四、五章补充:线代本质合集(B站:小崔说数)
视频1:线性空间 原视频:【线性代数的本质】向量空间、基向量的几何解释_哔哩哔哩_bilibili 很多同学在学习线性代数的时候,会遇到一个困扰,就是不知道什么是线性空间。...

2025年贵州省职业院校技能大赛信息安全管理与评估赛项规程
贵州省职业院校技能大赛赛项规程 赛项名称: 信息安全管理与评估 英文名称: Information Security Management and Evaluation 赛项组别: 高职组 赛项编号: GZ032 1 2 一、赛项信息 赛项类别 囚每年赛 □隔年赛(□单数年…...

松鼠状态机流转-@Transit
疑问 状态from to合法性校验,都是在代码中手动进行的吗,不是状态机自动进行的? 注解中from状态,代表当前状态 和谁校验:上下文中初始状态 怎么根据注解找到执行方法的 分析代码,创建运单,怎…...

微信小程序调用 WebAssembly 烹饪指南
我们都是在夜里崩溃过的俗人,所幸终会天亮。明天就是新的开始,我们会变得与昨天不同。 一、Rust 导出 wasm 参考 wasm-bindgen 官方指南 https://wasm.rust-lang.net.cn/wasm-bindgen/introduction.html wasm-bindgen,这是一个 Rust 库和 CLI…...
)
# LeetCode Problem 2038: 如果相邻两个颜色均相同则删除当前颜色 (Winner of the Game)
LeetCode Problem 2038: 如果相邻两个颜色均相同则删除当前颜色 (Winner of the Game) 在本篇博客中,我们将深入探讨 LeetCode 第2038题——如果相邻两个颜色均相同则删除当前颜色。该问题涉及字符串处理与游戏策略,旨在考察如何在给定规则下判断游戏的…...

Redis面试相关
Redis开篇 使用场景 缓存 缓存穿透 解决方法一: 方法二: 通过多次hash来获取对应的值。 小结 缓存击穿 缓存雪崩 打油诗 双写一致性 两种不同的要求 强一致 读锁代码 写锁代码 强一致,性能低。 延迟一致 方案一:消息队列 方…...

4.CSS文本属性
4.1文本颜色 div { color:red; } 属性值预定义的颜色值red、green、blue、pink十六进制#FF0000,#FF6600,#29D794RGB代码rgb(255,0,0)或rgb(100%,0%,0%) 4.2对齐文本 text-align 属性用于设置元素内文本内容的水平对齐方式。 div{ text-align:center; } 属性值解释left左对齐ri…...

Mongo高可用架构解决方案
Mongo主从复制哪些事(仅适用特定场景) 对数据强一致性要求不高的场景,一般微服务架构中不推荐 master节点可读可写操作,当数据有修改时,会将Oplog(操作日志)同步到所有的slave节点上。那么对于从节点来说仅只读,所有slave节点从master节点同步数据,然而从节点之间互相…...

Rabbitmq 业务异常与未手动确认场景及解决方案
消费端消费异常,业务异常 与 未手动确认是不是一个场景,因为执行完业务逻辑,再确认。解决方案就一个,就是重试一定次数,然后加入死信队列。还有就是消费重新放入队列,然后重新投递给其他消费者,…...

linux,centos7.6安装禅道
1.cd /opt 2.wget https://www.zentao.net/dl/zentao/18.5/ZenTaoPMS.18.5.zbox_64.tar.gz 3.tar xvzf ZenTaoPMS.18.5.zbox_64.tar.gz 4./opt/zbox/zbox --aport 4005 --mport 3307 start 安全组开启一下两个端口 –aport 4005:设置Apache启动端口为4005 –mport 3…...

java基础之代理
代理模式(Proxy Pattern) 简介 是一种结构型设计模式,主要用于为某对象提供一个代理对象,以控制对该对象的访问。通过引入一个代理对象来控制对原对象的访问。代理对象在客户端和目标对象之间充当中介,负责将客户端的…...

计算机网络——期末复习(6)期末考试样例2(含答案)
一、单项选择题(每题1分,共10小题,共计10分) 1.因特网多播采用的管理协议是( )协议。 A.UDP B.BGP C.IGMP D.TCP 2.采用CIDR时,某计算机的IP地址是202.35.79.88/19,该计算机所处子网的地址是( )。 A.202.35.0.…...

JavaScript 获取DOM对象
html的标签被js获取到之后就变成了js对象,对象里面包含了标签的属性和方法 。同一时间获取多个对象则会翻译一个数组,数组元素是对象 获取方法 1. const a document.getElementById("id"),根据标签的id来获取。因为id是唯一的、…...

一文讲明白朴素贝叶斯算法及其计算公式(入门普及)
1、贝叶斯算法 贝叶斯定理由英国数学家托马斯贝叶斯 ( Thomas Bayes) 提出的,用来描述两个条件概率之间的关系。通常,事件A在事件B 发生的条件下与事件 B 在事件 A 发生的条件下,它们两者的概率并不相同,但是它们两者之间存在一定…...
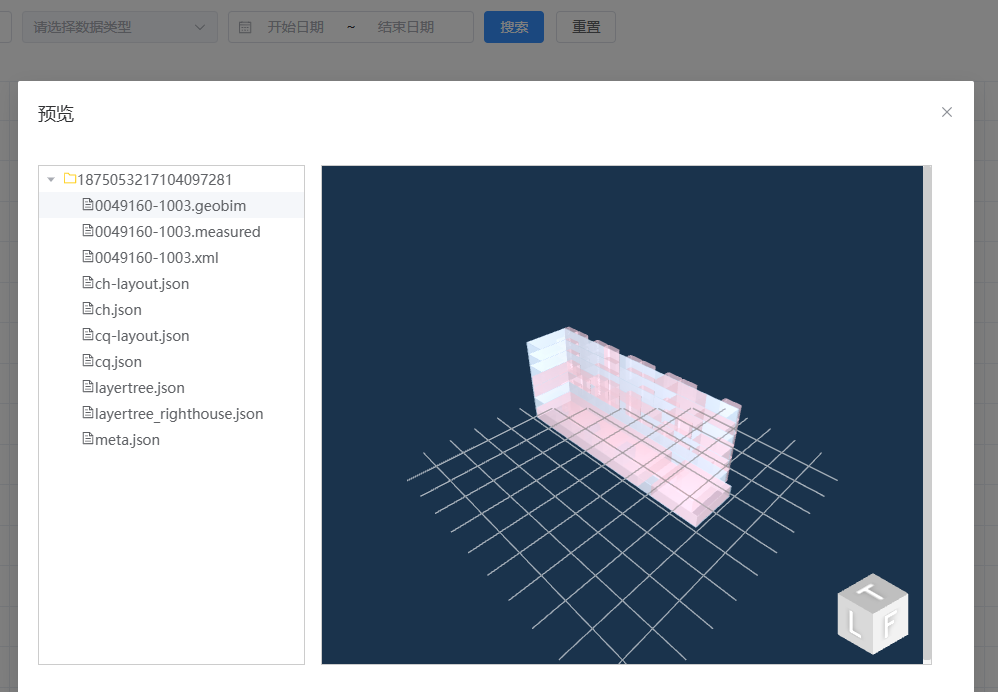
实际开发中,常见pdf|word|excel等文件的预览和下载
实际开发中,常见pdf|word|excel等文件的预览和下载 背景相关类型数据之间的转换1、File转Blob2、File转ArrayBuffer3、Blob转ArrayBuffer4、Blob转File5、ArrayBuffer转Blob6、ArrayBuffer转File 根据Blob/File类型生成可预览的Base64地址基于Blob类型的各种文件的下载各种类型…...

Python自学 - 递归函数
1 Python自学 - 递归函数 递归函数是一种在函数体内调用自己的函数,就像“左脚踩着右脚,再右脚踩着左脚… 嗯,你就可以上天了!”。递归函数虽然不能上天,但在处理某些场景时非常好用, 一种典型的场景就是遍…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
