数据结构知识收集尊享版(迅速了解回顾相关知识)
1、单链表、循环链表、双向链表,存储、逻辑结构
单链表、循环链表和双向链表都是线性表的链式存储结构,它们在存储和逻辑结构上有一些共同点和不同点。
存储结构
- 单链表:每个节点包含一个数据域和一个指针域,指针域指向下一个节点。最后一个节点的指针域为空(
NULL),表示链表的结束。 - 循环链表:与单链表类似,每个节点包含一个数据域和一个指针域,但最后一个节点的指针域指向链表的头节点,形成一个闭环。
- 双向链表:每个节点包含一个数据域和两个指针域,一个指向前驱节点,一个指向后继节点。头节点的前驱指针为空,尾节点的后继指针为空。
逻辑结构
- 单链表:
- 优点:插入和删除操作只需要修改指针,不需要移动元素,时间复杂度为 (O(1))。
- 缺点:只能从头节点开始遍历,查找某个节点需要 (O(n)) 的时间复杂度。
- 循环链表:
- 优点:可以方便地从任意节点开始遍历整个链表,适合某些需要循环操作的场景(如循环队列)。
- 缺点:查找某个节点的时间复杂度仍然是 (O(n)),但可以避免链表为空时的特殊情况处理。
- 双向链表:
- 优点:可以从任意节点向前或向后遍历,插入和删除操作更加灵活,时间复杂度为 (O(1))。
- 缺点:每个节点需要额外的指针空间,占用更多的内存。
应用场景
- 单链表:适用于需要频繁插入和删除操作,且不需要频繁查找的场景。
- 循环链表:适用于需要循环操作的场景,如循环队列、圆形游戏等。
- 双向链表:适用于需要频繁双向遍历的场景,如浏览器的前进后退功能、某些双向队列等。
2、栈、循环队列,元素个数判断、空/非空判断、多次进出后存储情况
栈和循环队列也都是线性数据结构,但它们在元素的进出顺序和存储方式上有所不同。
栈
- 元素个数判断:栈的元素个数可以通过一个计数器来记录,每次入栈时计数器加1,出栈时计数器减1。
- 空/非空判断:
- 空判断:如果计数器为0,则栈为空。
- 非空判断:如果计数器大于0,则栈非空。
- 多次进出后的存储情况:
- 栈遵循后进先出(LIFO)的原则,即最后进入的元素最先被取出。
- 多次进出后,栈顶元素始终是最近一次入栈且未被取出的元素。
- 如果栈的容量有限,多次进出时需要注意栈满的情况,防止溢出。
循环队列
- 元素个数判断:循环队列的元素个数可以通过队尾指针和队首指针的差值来计算,但需要注意循环的情况。
- 如果队尾指针大于队首指针,元素个数为
rear - front。 - 如果队尾指针小于队首指针,元素个数为
rear - front + capacity,其中capacity是队列的容量。
- 如果队尾指针大于队首指针,元素个数为
- 空/非空判断:
- 空判断:如果队首指针等于队尾指针,则队列为空。
- 非空判断:如果队首指针不等于队尾指针,则队列非空。
- 多次进出后的存储情况:
- 循环队列遵循先进先出(FIFO)的原则,即先进入的元素最先被取出。
- 多次进出后,队首指针始终指向队列的第一个元素,队尾指针指向队列最后一个元素的下一个位置。
- 为了避免队列满时的判断错误,通常会牺牲一个存储空间来区分队列满和队列空的情况。例如,当
(rear + 1) % capacity == front时,队列满。
应用场景
- 栈:适用于需要回溯或撤销操作的场景,如函数调用的堆栈、浏览器的后退功能、括号匹配等。
- 循环队列:适用于需要循环操作的场景,如任务调度、缓冲区管理等。
注意事项
- 栈:在使用栈时,需要注意栈溢出的情况,尤其是在递归调用深度较大的情况下。
- 循环队列:在使用循环队列时,需要注意队列满和队列空的判断条件,避免误判。
3、串next求取、BF及KMP模式匹配过程
串的next数组求取
KMP算法中的next数组用于记录模式串中每个字符的前缀和后缀的最大相同长度。具体求取过程如下:
-
初始化:
next[0] = -1,表示第一个字符没有前缀和后缀可以比较。- 初始化两个指针
j和k,其中j用于遍历模式串,k用于记录前缀的长度。
-
计算next数组:
- 当
k == -1或者模式串的第j个字符与第k个字符相等时,next[j] = k,然后j和k都加1。 - 如果不相等,则
k更新为next[k],继续比较。
- 当
-
循环结束:
- 当
j遍历完整个模式串时,next数组计算完成。
- 当
BF模式匹配过程
BF算法(暴力匹配算法)是最简单的字符串匹配算法:
-
初始化:
- 设置两个指针
i和j,分别指向文本串和模式串的起始位置。
- 设置两个指针
-
匹配过程:
- 如果
text[i]和pattern[j]相等,则i和j都向后移动一位。 - 如果不相等,则将模式串向后移动一位,即
j重置为0,i指向下一个字符。
- 如果
-
匹配成功:
- 当
j达到模式串的末尾时,表示匹配成功,返回i - j作为匹配位置的起始索引。
- 当
-
匹配失败:
- 如果
i遍历完文本串,则表示没有匹配到模式串。
- 如果
KMP模式匹配过程
KMP算法利用next数组来优化匹配过程:
-
初始化:
- 设置两个指针
i和j,分别指向文本串和模式串的起始位置。 - 计算模式串的next数组。
- 设置两个指针
-
匹配过程:
- 如果
text[i]和pattern[j]相等,则i和j都向后移动一位。 - 如果不相等,则
j更新为next[j],i保持不变。
- 如果
-
匹配成功:
- 当
j达到模式串的末尾时,表示匹配成功,返回i - j作为匹配位置的起始索引。
- 当
-
匹配失败:
- 如果
i遍历完文本串,则表示没有匹配到模式串。
- 如果
KMP算法通过next数组减少了不必要的比较,从而提高了匹配效率。
4、二维数组存储计算
二维数组在计算机中通常以一维数组的形式存储,主要有两种存储方式:按行存储和按列存储。不同的存储方式会影响元素的访问和计算方式。以下是对这两种存储方式的详细说明:
按行存储(Row-major Order)
- 存储方式:二维数组的元素按行顺序存储在一维数组中。首先存储第一行的所有元素,然后是第二行的所有元素,依此类推。
- 地址计算:假设二维数组
A的大小为m x n,每个元素占用size个字节,基地址为base,则元素A[i][j]的地址可以通过以下公式计算:
Address(A[i][j])=base+(i×n+j)×size
其中,i是行索引,j是列索引。
按列存储(Column-major Order)
- 存储方式:二维数组的元素按列顺序存储在一维数组中。首先存储第一列的所有元素,然后是第二列的所有元素,依此类推。
- 地址计算:同样假设二维数组
A的大小为m x n,每个元素占用size个字节,基地址为base,则元素A[i][j]的地址可以通过以下公式计算:
Address(A[i][j])=base+(j×m+i)×size
其中,i是行索引,j是列索引.
示例
假设有一个二维数组 A,大小为 3 x 4,每个元素占用 4 个字节,基地址为 1000。按行存储和按列存储的地址计算如下:
-
按行存储:
A[1][2]的地址:
Address(A[1][2])=1000+(1×4+2)×4=1000+24=1024
-
按列存储:
A[1][2]的地址:
Address(A[1][2])=1000+(2×3+1)×4=1000+28=1028
树的遍历
树的遍历主要有三种方式:先序遍历、中序遍历和后序遍历。这些遍历方式通常用于二叉树,但也可以扩展到多叉树。
先序遍历
- 定义:先访问根节点,然后递归地先序遍历左子树,最后递归地先序遍历右子树。
- 过程:
- 访问根节点。
- 先序遍历左子树。
- 先序遍历右子树。
中序遍历
- 定义:先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。
- 过程:
- 中序遍历左子树。
- 访问根节点。
- 中序遍历右子树。
后序遍历
- 定义:先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。
- 过程:
- 后序遍历左子树。
- 后序遍历右子树。
- 访问根节点.
二叉树的顺序存储
二叉树的顺序存储是将二叉树的节点存储在一个一维数组中,按照从上到下、从左到右的顺序排列。这种存储方式适用于完全二叉树和满二叉树,但对于一般的二叉树可能会浪费空间。
存储规则
- 根节点:存储在数组的第一个位置(索引为0)。
- 左子节点:对于索引为
i的节点,其左子节点的索引为2i + 1。 - 右子节点:对于索引为
i的节点,其右子节点的索引为2i + 2。 - 父节点:对于索引为
i的节点,其父节点的索引为(i - 1) / 2(向下取整).
示例
假设有一个二叉树,其节点值如下:
1/ \2 3/ \ \4 5 6
其顺序存储的数组为 [1, 2, 3, 4, 5, 6]。
应用场景
- 先序遍历:常用于复制树结构、打印树结构等。
- 中序遍历:对于二叉搜索树,中序遍历可以得到节点值的有序序列。
- 后序遍历:常用于计算树的大小、删除树等。
- 顺序存储:适用于完全二叉树和满二叉树,如堆的实现.
注意事项
- 遍历递归实现:递归实现简单直观,但可能会导致栈溢出,尤其是在树的深度较大时。
- 非递归实现:可以使用栈来实现非递归遍历,避免递归调用的开销。
- 顺序存储空间浪费:对于一般的二叉树,顺序存储可能会浪费大量空间,因为需要为不存在的节点预留位置。
哈夫曼树的构建
哈夫曼树是一种用于数据压缩的无损编码方法,其构建过程如下:
-
初始化:
- 将每个字符及其出现的频率视为一个节点,初始化一个优先队列(最小堆),将所有节点加入队列。
-
构建过程:
- 从优先队列中取出两个权值最小的节点。
- 创建一个新的节点,其权值为两个取出节点的权值之和。
- 将新节点的左子节点和右子节点分别设置为取出的两个节点。
- 将新节点重新加入优先队列。
- 重复上述步骤,直到优先队列中只剩下一个节点,该节点即为哈夫曼树的根节点。
哈夫曼编码的求取
哈夫曼编码是通过哈夫曼树来确定每个字符的编码,具体步骤如下:
-
初始化:
- 从哈夫曼树的根节点开始,初始化一个空字符串作为编码路径。
-
编码过程:
- 从根节点向叶子节点遍历:
- 如果向左子节点移动,则在编码路径上添加“0”。
- 如果向右子节点移动,则在编码路径上添加“1”。
- 当到达叶子节点时,该叶子节点对应的字符的编码即为当前的编码路径。
- 从根节点向叶子节点遍历:
-
编码结果:
- 每个字符的哈夫曼编码是唯一的,且通常较短的编码分配给出现频率较高的字符。
示例
假设有一组字符及其频率:A(5), B(9), C(12), D(13), E(16), F(45),构建哈夫曼树并求取编码的过程如下:
-
构建哈夫曼树:
- 初始优先队列:
A(5), B(9), C(12), D(13), E(16), F(45) - 取出
A(5)和B(9),创建新节点AB(14),加入队列:AB(14), C(12), D(13), E(16), F(45) - 继续合并,直到构建完整棵树。
- 初始优先队列:
-
求取编码:
- 从根节点开始遍历,最终得到每个字符的编码:
F: 0C: 100D: 101A: 1100B: 1101E: 111
- 从根节点开始遍历,最终得到每个字符的编码:
邻接矩阵和邻接表
邻接矩阵
- 定义:邻接矩阵是一个二维数组,用于表示图中顶点之间的连接关系。
- 存储方式:
- 对于无向图,邻接矩阵是对称的。
A[i][j]表示顶点i和顶点j之间的边的权重。如果i和j之间没有边,则A[i][j]为无穷大或一个特定的值(如0)。 - 对于有向图,邻接矩阵不一定对称。
A[i][j]表示从顶点i到顶点j的边的权重。
- 对于无向图,邻接矩阵是对称的。
- 优点:
- 可以快速判断两个顶点之间是否存在边。
- 缺点:
- 空间复杂度高,尤其是对于稀疏图,会浪费大量空间。
邻接表
- 定义:邻接表是一个数组,每个数组元素是一个链表,用于存储与该顶点相邻的所有顶点。
- 存储方式:
- 对于无向图,每个顶点的邻接表中存储与其相连的所有顶点。
- 对于有向图,每个顶点的邻接表中存储其所有出边的目标顶点。
- 优点:
- 空间复杂度低,适合稀疏图。
- 缺点:
- 判断两个顶点之间是否存在边需要遍历链表,时间复杂度较高。
深度优先遍历(DFS)和广度优先遍历(BFS)
深度优先遍历(DFS)
- 过程:
- 从一个顶点开始,沿着一条路径尽可能深地搜索,直到无法继续前进。
- 回溯到上一个顶点,继续搜索其他未访问的路径。
- 实现:
- 使用递归或栈来实现。
- 标记已访问的顶点,避免重复访问。
- 应用:
- 用于寻找路径、检测图的连通性等。
广度优先遍历(BFS)
- 过程:
- 从一个顶点开始,逐层访问其所有邻接顶点。
- 访问完一层的所有顶点后,再访问下一层的顶点。
- 实现:
- 使用队列来实现。
- 标记已访问的顶点,避免重复访问。
- 应用:
- 用于寻找最短路径、检测图的连通性等。
最小生成树求取
Prim算法
- 过程:
- 从任意一个顶点开始,将其加入生成树。
- 在生成树的顶点集合中,选择一条连接生成树和非生成树顶点的最小权值边,将该边的非生成树顶点加入生成树。
- 重复上述步骤,直到所有顶点都加入生成树。
- 实现:
- 使用优先队列(最小堆)来优化选择最小权值边的过程。
- 应用:
- 适用于稠密图,因为每次只需要选择一个顶点。
Kruskal算法
- 过程:
- 将图中的所有边按权值从小到大排序。
- 依次选择权值最小的边,如果该边的两个顶点不在同一个连通分量中,则将其加入生成树。
- 重复上述步骤,直到生成树包含所有顶点。
- 实现:
- 使用并查集来检测连通分量。
- 应用:
- 适用于稀疏图,因为每次只需要选择一条边.
这两种算法都可以有效地求取无向图的最小生成树,选择哪种算法取决于图的稠密程度和具体的应用场景。
二叉排序树(也称为二叉查找树或二叉搜索树)是一种特殊的二叉树,其中每个节点的值大于其左子树中所有节点的值,小于其右子树中所有节点的值。以下是关于二叉排序树的生成和查找的详细说明:
二叉排序树的生成
插入过程
- 步骤:
- 初始化:从根节点开始。
- 比较:将要插入的值与当前节点的值进行比较。
- 如果要插入的值小于当前节点的值,则移动到当前节点的左子节点。
- 如果要插入的值大于当前节点的值,则移动到当前节点的右子节点。
- 递归:重复上述比较和移动过程,直到找到一个空的子节点位置。
- 插入:在找到的空位置插入新节点。
示例
假设我们要将以下值依次插入到一个空的二叉排序树中:50, 30, 20, 40, 70, 60, 80。
- 插入
50:作为根节点。 - 插入
30:小于50,插入到50的左子节点。 - 插入
20:小于30,插入到30的左子节点。 - 插入
40:大于30,插入到30的右子节点。 - 插入
70:大于50,插入到50的右子节点。 - 插入
60:小于70,插入到70的左子节点。 - 插入
80:大于70,插入到70的右子节点。
最终生成的二叉排序树如下:
50/ \30 70/ \ / \20 40 60 80
二叉排序树的查找
查找过程
- 步骤:
- 初始化:从根节点开始。
- 比较:将要查找的值与当前节点的值进行比较。
- 如果要查找的值等于当前节点的值,则查找成功,返回当前节点。
- 如果要查找的值小于当前节点的值,则移动到当前节点的左子节点。
- 如果要查找的值大于当前节点的值,则移动到当前节点的右子节点。
- 递归:重复上述比较和移动过程,直到找到目标节点或到达空节点。
- 查找失败:如果到达空节点,则表示查找失败,返回空。
示例
假设我们要在上述生成的二叉排序树中查找值 40。
- 从根节点
50开始。 40小于50,移动到左子节点30。40大于30,移动到右子节点40。- 找到目标节点
40,查找成功。
如果要查找值 45,则:
- 从根节点
50开始。 45小于50,移动到左子节点30。45大于30,移动到右子节点40。45大于40,但40的右子节点为空,查找失败.
冒泡排序(Bubble Sort)
- 过程:
- 比较相邻的元素,如果第一个元素大于第二个元素,就交换它们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对,这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
选择排序(Selection Sort)
- 过程:
- 在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置。
- 从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
插入排序(Insertion Sort)
- 过程:
- 从第一个元素开始,该元素可以认为已经被排序。
- 取出下一个元素,在已经排序的元素序列中从后向前扫描。
- 如果该元素(已排序)大于新元素,将该元素移到下一位置。
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置。
- 将新元素插入到该位置后。
- 重复步骤2~5。
希尔排序(Shell Sort)
-
过程:
1.选择一个增量序列 t1,t2,….,tk,其中 t> ti+1,且 tk =1。
2.按增量序列个数 k,对序列进行 k 趟插入排序。
3.每趟排序,根据对应的增量 t,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度
快速排序(Quick Sort)
- 过程:
- 选择一个基准值(pivot),通常选择序列的第一个元素或最后一个元素。
- 将所有比基准值小的元素放到基准前面,所有比基准值大的元素放到基准后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数组的中间位置。
- 递归地将小于基准值元素的子数组和大于基准值元素的子数组排序。
归并排序(Merge Sort)
- 过程:
- 将序列每相邻两个数字进行归并操作,形成 [n/2] 个序列,排序后每个序列包含两个元素。
- 将上述序列再次归并,形成[n/4]个序列,每个序列大概包含四个元素。
- 重复上述操作,直到所有元素排序完毕。
堆排序(Heap Sort)
- 过程:
- 将待排序序列构建成一个大顶堆,此时,整个序列的最大值就是堆顶元素。
- 将堆顶元素与末尾元素交换,将最大元素“沉”到数组末端。
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行,直至整个序列有序。
基数排序(Radix Sort)
- 过程:
- 将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。
- 从最低位开始,依次进行稳定排序(通常使用计数排序)。
- 重复上述过程,直到最高位排序完成。
桶排序(Bucket Sort)
- 过程:
- 设置一个定量的数组当作空桶。
- 遍历输入数据,并且把数据根据其特征值放入对应的桶中。
- 对每个不为空的桶进行排序,可以使用其他排序算法,或者递归地使用桶排序。
- 按顺序把桶中的数据拼起来。
哈希表是一种通过哈希函数将键(key)映射到值(value)的数据结构,具有高效的查找、插入和删除操作。当哈希冲突发生时,需要采用一定的解决方法。线性探测法和二次探测法是两种常用的解决哈希冲突的方法。
哈希表求取
-
选择哈希函数:
- 哈希函数将键映射到哈希表中的一个索引位置。常见的哈希函数包括除法哈希、乘法哈希等。
- 例如,除法哈希函数:
hash(key) = key % table_size,其中table_size是哈希表的大小。
-
处理哈希冲突:
- 当两个不同的键映射到同一个索引位置时,发生哈希冲突。需要采用一定的方法解决冲突,如链表法、线性探测法、二次探测法等。
线性探测法
-
基本思想:
- 当发生哈希冲突时,线性探测法从冲突位置开始,线性地向后探测,直到找到一个空的槽位。
- 探测序列是线性的,即
h(key) + i,其中i是探测次数,从0开始递增。
-
插入过程:
- 计算键的哈希值
h(key)。 - 如果
h(key)位置为空,则直接插入。 - 如果
h(key)位置已被占用,则从h(key)开始线性探测,直到找到一个空的槽位插入。
- 计算键的哈希值
-
查找过程:
- 计算键的哈希值
h(key)。 - 从
h(key)开始线性探测,直到找到目标键或探测到一个空槽位(表示查找失败)。
- 计算键的哈希值
二次探测法
-
基本思想:
- 当发生哈希冲突时,二次探测法从冲突位置开始,按照二次方的步长进行探测,直到找到一个空的槽位。
- 探测序列是二次的,即
h(key) + i^2,其中i是探测次数,从1开始递增。
-
插入过程:
- 计算键的哈希值
h(key)。 - 如果
h(key)位置为空,则直接插入。 - 如果
h(key)位置已被占用,则从h(key)开始二次探测,直到找到一个空的槽位插入。
- 计算键的哈希值
-
查找过程:
- 计算键的哈希值
h(key)。 - 从
h(key)开始二次探测,直到找到目标键或探测到一个空槽位(表示查找失败)。
- 计算键的哈希值
优缺点比较
-
线性探测法:
- 优点:实现简单。
- 缺点:容易产生聚集现象,即多个键聚集在连续的槽位中,导致探测长度增加,性能下降。
-
二次探测法:
- 优点:可以减少聚集现象,探测序列更加分散。
- 缺点:实现相对复杂,且在某些情况下可能会探测到重复的位置(如当
i和j的平方模table_size相等时)。
应用场景
- 线性探测法:适用于哈希表较小且负载因子较低的情况,因为聚集现象对性能的影响较小。
- 二次探测法:适用于哈希表较大且负载因子较高的情况,可以更好地分散键的分布,提高性能。
相关文章:
)
数据结构知识收集尊享版(迅速了解回顾相关知识)
1、单链表、循环链表、双向链表,存储、逻辑结构 单链表、循环链表和双向链表都是线性表的链式存储结构,它们在存储和逻辑结构上有一些共同点和不同点。 存储结构 单链表:每个节点包含一个数据域和一个指针域,指针域指向下一个节…...

SpringMVC启动与请求处理流程解析
目录 SpringMVC的基本结构 1.MVC简介 2.基本结构 什么是Handler? 什么是HandlerMapping? 什么是HandlerAdapter? RequestMapping方法参数解析 DispatcherServlet的init()方法 DispatcherServlet的doService()方法 SpringBoot整合SpringMVC …...

C++ 日志库 spdlog 使用教程
Spdlog是一个快速、异步、线程安全的C日志库,他可以方便地记录应用程序的运行状态,并提供多种输出格式。官网:https://github.com/gabime/spdlog 安装教程可以参考:https://blog.csdn.net/Harrytsz/article/details/144887297 S…...

`http_port_t
http_port_t 是 SELinux(Security-Enhanced Linux)中的一种端口类型标签,用于标识哪些端口可以被 HTTP 和 HTTPS 服务使用。SELinux 是一种强制访问控制(MAC)安全模块,它通过定义安全策略来限制进程对系统资…...

SpringBoot中实现拦截器和过滤器
【SpringBoot中实现过滤器和拦截器】 1.过滤器和拦截器简述 过滤器Filter和拦截器Interceptor,在功能方面很类似,但在具体实现方面差距还是比较大的。 2.过滤器的配置 2.1 自定义过滤器,实现Filter接口(SpringBoot 3.0 开始,jak…...

不锈钢均温板结合强力粘合技术革新手机内部架构
摘要: 本文介绍了一种创新性的手机内部架构设计方案,其中不锈钢均温板不仅作为高效的散热元件,还充当了手机中框的主要结构件。通过使用强力不可拆胶水将主板、尾插和其他关键部件直接粘合到均温板上,该方案实现了更为紧密的热耦合…...

Docker安装使用
文章目录 Docker安装Docker的基础使用搜索&拉取镜像 Docker的生命周期利用Docker切换不同OSDocker容器 镜像的保存&分享Docker存储Docker网络 Docker安装 更新apt索引 sudo apt-get update添加Docker所需要的依赖 apt-get install ca-certificates curl gnupg lsb-r…...

React 如何进行路由变化监听
一、使用react-router库(以react-router-dom为例) 1. 历史(history)对象监听 1.1 原理 react-router内部使用history对象来管理路由历史记录。可以通过访问history对象来监听路由变化。在基于类的组件中,可以通过组…...

Unity UGUI使用技巧与经验总结(不定期更新)
Text自动缩放参考连接: Unity -UGUI中Text文本框的自动调整,字体大小的自适应调节_unity添加的字体大小锁定-CSDN博客 Toggle按钮选择时,显示对应的UI界面: 为Toggle组件的On Value Change事件添加对需要显示的对象的SetActive…...

中国乡镇界shp全境arcgis格式shp数据乡镇名称下载后内容测评
下载乡镇界shp链接:https://download.csdn.net/download/zhongguonanren99/19354855 标题中的“中国乡镇界shp全境arcgis格式shp数据乡镇名称2012年”揭示了这个数据集的核心内容。它是一个地理信息系统(GIS)数据,具体来说是使用…...
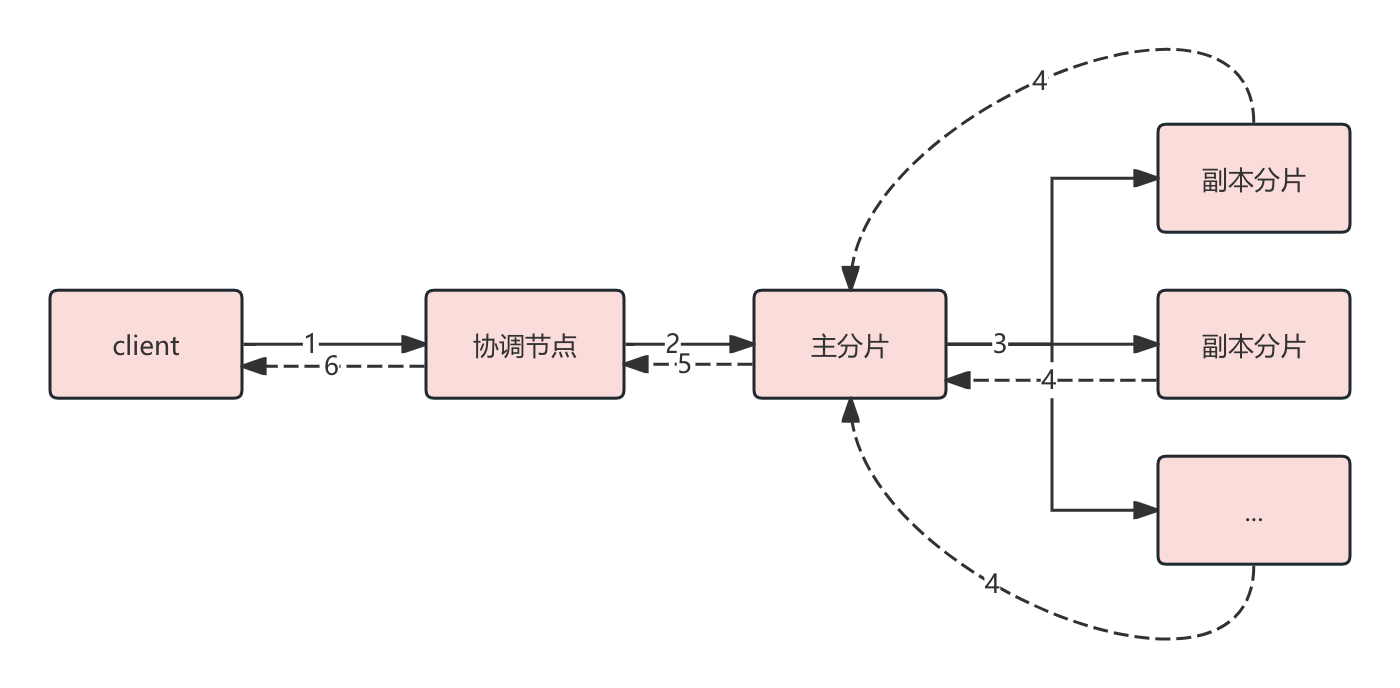
第 31 章 - 源码篇 - Elasticsearch 写入流程深入分析
写入源码分析 接收与处理 请求首先会被 Netty4HttpServerTransport 接收,接着交由 RestController 进行路由分发。 private void tryAllHandlers(final RestRequest request, final RestChannel channel, final ThreadContext threadContext) throws Exception {…...

node.js下载、安装、设置国内镜像源(永久)(Windows11)
目录 node-v20.18.0-x64 工具下载安装设置国内镜像源(永久) node-v20.18.0-x64 工具 系统:Windows 11 下载 官网https://nodejs.org/zh-cn/download/package-manager 版本我是跟着老师选的node-v20.18.0-x64如图选择 Windows、x64、v2…...

小于n的最大数 - 贪心算法 - C++
字节经典面试题 给定一个整数n,并从1~9中给定若干个可以使用的数字,根据上述两个条件,得到每一位都为给定可使用数字的、最大的小于整数n的数,例如,给定可以使用的数字为 {2,3,8} 三个数:给定 n3589&#x…...

【顶刊TPAMI 2025】多头编码(MHE)之极限分类 Part 3:算法实现
目录 1 三种多头编码(MHE)实现1.1 多头乘积(MHP)1.2 多头级联(MHC)1.3 多头采样(MHS)1.4 标签分解策略 论文:Multi-Head Encoding for Extreme Label Classification 作者…...

解决CentOS 8 YUM源更新后报错问题:无法下载AppStream仓库元数据
背景介绍 在尝试更新CentOS 8的YUM源以使用阿里云镜像时,遇到了Failed to download metadata for repo appstream的错误。此错误通常出现在执行yum clean all && yum makecache命令之后,表明系统无法从指定的URL获取AppStream仓库的元数据。本文…...

[python3]Excel解析库-openpyxl
https://openpyxl.readthedocs.io/en/stable/ openpyxl 是一个用于读写 Excel 2010 xlsx/xlsm/xltx/xltm 文件的 Python 库。它允许开发者创建、修改和保存电子表格,而无需依赖 Microsoft Excel 软件本身。openpyxl 支持读取和写入 Excel 的工作簿(Work…...

Docker 远程访问完整配置教程以及核心参数理解
Docker 远程访问完整配置教程 以下是配置 Docker 支持远程访问的完整教程,包括参数说明、配置修改、云服务器安全组设置、主机防火墙配置,以及验证远程访问的详细步骤。 1. 理解 -H fd:// 参数的作用(理解了以后容易理解后面的操作ÿ…...

王老吉药业SRM系统上线 携手隆道共启战略合作新篇章
12月27日,广州王老吉药业股份有限公司(简称“王老吉药业”)SRM项目上线启动会,在王老吉科普教育基地——“吉园”隆重举行。广药集团纪委主任陈耕、王老吉药业总工程师黄晓丹、隆道公司总裁吴树贵、项目经理赵耀、供应商代表郭伟及…...

MyBatis 配置文件全解析
一、MyBatis 配置文件为何至关重要? 在 Java 后端开发领域,MyBatis 作为一款广受欢迎的持久层框架,极大地简化了数据库操作。而 MyBatis 配置文件,恰似整个框架的 “神经中枢”,掌控着其运行的方方面面,对…...

unity学习6:unity的3D项目的基本界面和菜单
目录 1 unity界面的基本认识 1.1 file 文件 1.2 edit 编辑/操作 1.3 Assets 1.4 gameobject 游戏对象 1.5 组件 1.6 windows 2 这些部分之间的关系 2.1 关联1: Assets & Project 2.2 关联2:gameobject & component 2.3 关联3…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
