第四章.误差反向传播法—ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
第四章.误差反向传播法
4.2 ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
1.ReLU层
1).公式

2).导数:
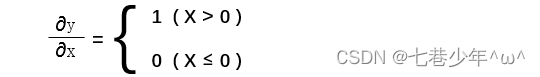
3).计算图:

4).实现:
class ReLU:def __init__(self):self.mask = None# 正向传播def forward(self, x):self.mask = (x <= 0) # 输入值是否≤0,返回值是由True/False构成的Numpy数组out = x.copy()out[self.mask] = 0 # mask中的元素为True的地方置为0return out# 反向传播def backward(self, dout):dout[self.mask] = 0dx = doutreturn dx2.Sigmoid层
1).公式:
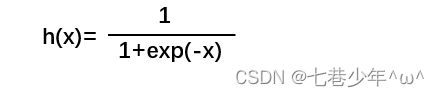
2).计算图:

- 简洁版
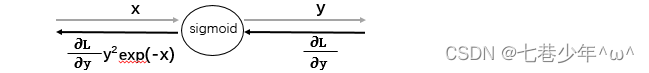
3).导数:

4).实现:
import numpy as npclass Sigmoid:def __init__(self):self.out = None# 正向传播def forward(self, x):out = 1 / (1 + np.exp(-x))self.out = outreturn out# 反向传播def backward(self, dout):dx = dout * (1.0 - self.out) * self.outreturn dx3.Affine层
- 神经网络的正向传播中进行的矩阵乘积运算在几何学领域被称为“仿射变化”,因此,将进行仿射变化的处理实现为Affine层。
- 几何中,仿射变换包括一次线性变换和一次平移,分别对应神经网络的加权和运算和加偏置运算。
1).计算图:
-
单个数据的Affine层:
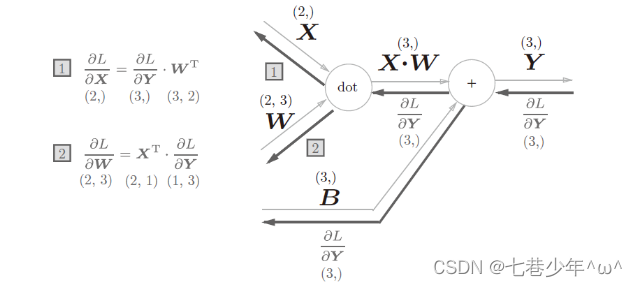
-
批版本的Affine层:
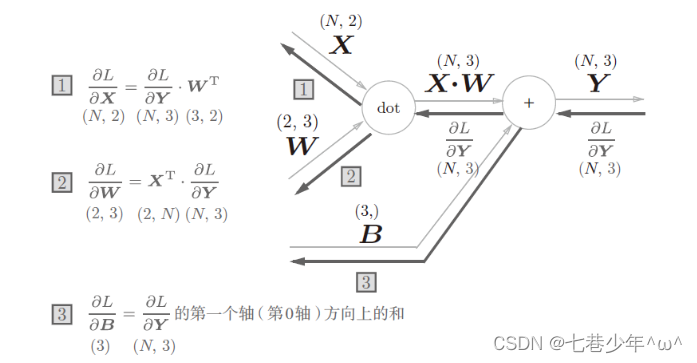
2).实现:
·未考虑输入张量的情况:
import numpy as npclass Affine:def __init__(self, W, b):self.W = Wself.b = bself.x = Noneself.dw = Noneself.db = None# 正向传播def forward(self, x):self.x = xout = np.dot(self.x, self.W) + self.breturn out# 反向传播def backward(self, dout):dx = np.dot(dout, self.W.T)self.dw = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)return dx·考虑输入张量的情况 (张量就是多维数据)
import numpy as npclass Affine:def __init__(self, W, b):self.W = Wself.b = bself.x = Noneself.original_x_shape = None# 权重和偏置参数的导数self.dW = Noneself.db = Nonedef forward(self, x):# 对应张量self.original_x_shape = x.shape # 例如:x.shape=(209, 64, 64, 3)x = x.reshape(x.shape[0], -1) # x=(209, 64*64*3)self.x = xout = np.dot(self.x, self.W) + self.breturn outdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)return dx4.Softmax-with-Loss层
- 神经网络中进行的处理有推理和学习两个阶段,推理阶段通常不适用softmax层,学习阶段需要使用softmax层。
1).计算图:

2).实现:
import numpy as npclass SoftmaxWithLoss:def __init__(self):self.loss = None # 损失self.y = None # softmax的输出self.t = None # 监督数据(one_hot vector)# 输出层函数:softmaxdef softmax(x):if x.ndim == 2:x = x.Tx = x - np.max(x, axis=0)y = np.exp(x) / np.sum(np.exp(x), axis=0)return y.Tx = x - np.max(x) # 溢出对策return np.exp(x) / np.sum(np.exp(x))# 交叉熵误差def cross_entropy_error(y, t):if y.ndim == 1:t = t.reshape(1, t.size)y = y.reshape(1, y.size)# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引if t.size == y.size:t = t.argmax(axis=1)batch_size = y.shape[0]return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size# 正向传播def forward(self, x, t):self.t = tself.y = self.softmax(x)self.loss = self.cross_entropy_error(self.y, self.t)return self.loss# 反向传播def backward(self, dout=1):batch_size = self.t.shape[0]if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况dx = (self.y - self.t) / batch_sizeelse:dx = self.y.copy()dx[np.arange(batch_size), self.t] -= 1dx = dx / batch_sizereturn dx相关文章:

第四章.误差反向传播法—ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
第四章.误差反向传播法 4.2 ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现 1.ReLU层 1).公式 2).导数: 3).计算图: 4).实现: class ReLU:def __init__(self):self.mask None# 正向传播def forward(self, x):self.mask (x < 0) # 输入…...
Python-第二天 Python基础语法
Python-第二天 Python基础语法一、 字面量1.1 常用的值类型1.1.1 字符串(string)二、注释2.1 注释的作用2.2 注释的分类三、变量3.1 什么是变量3.2 变量的特征四、数据类型4.1 数据类型4.2 type()语句4.3 type()语句的使用方式4.4 变量有类型吗ÿ…...
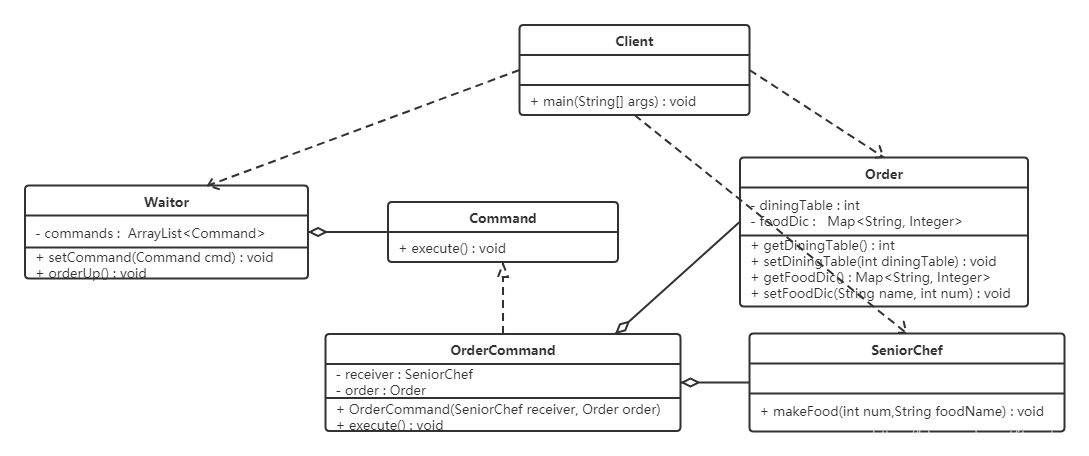
命令模式包含哪些主要角色?怎样实现命令?
命令模式包含以下主要角色:抽象命令类(Command)角色: 定义命令的接口,声明执行的方法。具体命令(Concrete Command)角色:具体的命令,实现命令接口;通常会持有…...

SpringCloud-Feign
Spring Cloud中集成Feign (只是笔记而已 其中有点命名啥的不对应,搜到了就划走吧) Feign--[feɪn]:Web 服务客户端,能够简化 HTTP 接口的调用。 没有Feign的之前服务提供者 package com.springcloudprovide.controller;import com.springclo…...

XCP实战系列介绍08-基于Vehicle Spy进行XCP测量的工程配置详解
本文框架 1.概述2. 工程配置步骤2.1 创建MEP工程2.1.1 添加A2L文件2.1.2 CAN收发ID配置2.2 MEP属性设置2.2.1 ECU属性设置2.2.2 MEP的Security设置2.3 DAQ设置2.3.1创建DAQ2.3.2 list中测量及标定量的添加和设置2.3.3 设置DAQ list中变量的event1.概述 在前面一篇文章《看了就…...

JVM调优几款好用的内存分析工具
对于高并发访问量的电商、物联网、金融、社交等系统来说,JVM内存优化是非常有必要的,可以提高系统的吞吐量和性能。通常调优的首选方式是减少FGC次数或者FGC时间,以避免系统过多地暂停。FGC达到理想值后,比如一天或者两天触发一次…...
Vue中路由缓存及activated与deactivated的详解
目录前言一,路由缓存1.1 引子1.2 路由缓存的方法1.2.1 keep-alive1.2.2 keep-alive标签中的include属性1.2.3 include中多组件的配置二,activated与deactivated2.1 引子2.2 介绍activated与deactivated2.3 解决需求三,整体代码总结前言 在Vu…...
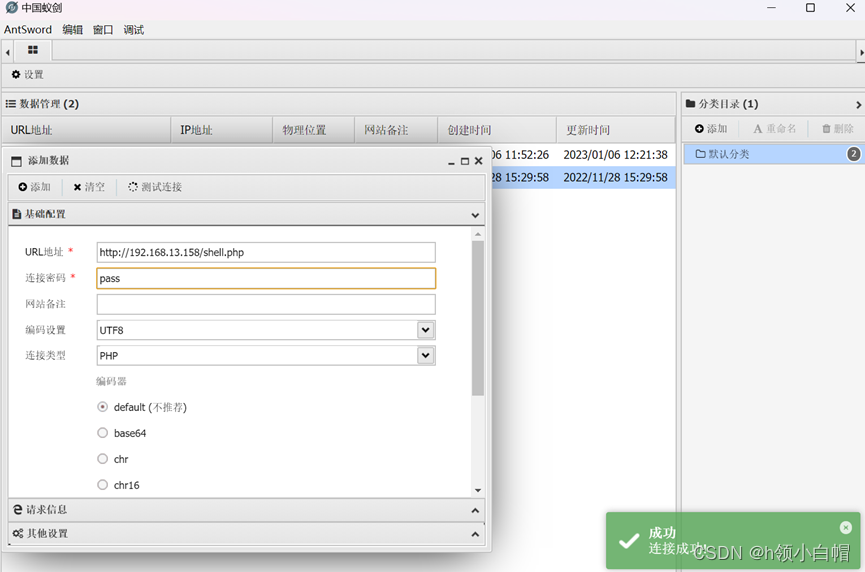
【漏洞复现】phpStudy 小皮 Windows面板 RCE漏洞
文章目录前言一、漏洞描述二、漏洞复现前言 本篇文章仅用于漏洞复现研究和学习,切勿从事非法攻击行为,切记! 一、漏洞描述 Phpstudy小皮面板存在RCE漏洞,通过分析和复现方式发现其实本质上是一个存储型XSS漏洞导致的RCE。通过系…...

跨域小样本系列2:常用数据集与任务设定详解
来源:投稿 作者:橡皮 编辑:学姐 带你学习跨域小样本系列1-简介篇 跨域小样本系列2-常用数据集与任务设定详解(本篇) 跨域小样本系列3:元学习方法解决CDFSL以及两篇SOTA论文讲解 跨域小样本系列4…...

HTML浪漫动态表白代码+音乐(附源码)
HTML浪漫表白求爱(附源码),内含4款浪漫的表白源码,可用于520,情人节,生日,求爱场景,下载直接使用。 直接上源码吧 一.红色爱心 1.效果 实际效果是动态的哦 2.源码 复制粘贴即可运行哦 <!DOCTYPE…...
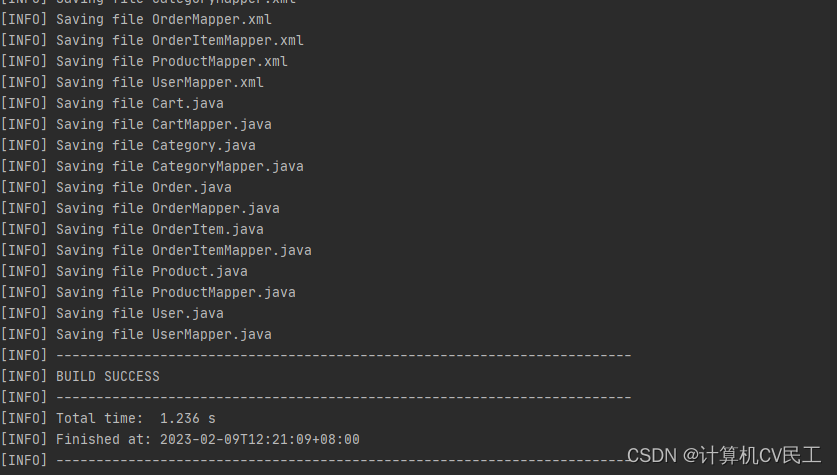
The last packet sent successfully to the server was 0 milliseconds ago. 解决办法
mybatis-generator-maven-plugin插件The last packet sent successfully to the server was 0 milliseconds agoYou must configure either the server or JDBC driver (via the serverTimezone configuration property) to use a more specifc time zone value if you want to…...
分布式高级篇1 —— 全文检索
Elasticsearch Elasticsearch简介一、基本概念1、index(索引)2、Type(类型)3、Document(文档)4、倒排索引二、Docker 安装 EL1、拉取镜像2、创建实例三、初步探索1、_cat2、索引一个文档(保存)3、查询文档3、更新文档4、删除文档&索引5、_bulk 批量 AP6、样本测试数据四、进…...

集成电路开发及应用-模拟数字部分专栏目录
三角波发生器电路图分析_XMJYBY的博客-CSDN博客运算放大器正反馈负反馈判别法_如何理解运算放大器的反馈机制,分哪几种_XMJYBY的博客-CSDN博客运算放大器实现多路同向反向加减运算电路公式推导(一)_反向减法运算电路_XMJYBY的博客-CSDN博客运算放大器实现多路同向反向加减运算电…...
)
ios使用SARUnArchiveANY 解压rar文件(oc和swift版本)
SARUnArchiveANY简介 开源库网址: https://github.com/saru2020/SARUnArchiveANY 简介: 一个iOS的非常有用的库来解压zip,.rar,7z文件。 他是以下库的简单集成: UnrarKitSSZipArchiveLzmaSDKObjC (7z) 需要注意的是…...
)
【Python学习笔记】21.Python3 函数(2)
前言 本章介绍调用函数时可使用的正式参数。 参数 以下是调用函数时可使用的正式参数类型: 必需参数关键字参数默认参数不定长参数 必需参数 必需参数须以正确的顺序传入函数。调用时的数量必须和声明时的一样。 调用 printme() 函数,你必须传入一…...

day57回文子串_最长回文子序列
力扣647.回文子串 题目链接:https://leetcode.cn/problems/palindromic-substrings/ 思路 dp数组含义 dp[i][j]:以s[i]为开头,s[j]为结尾的子串是否是回文子串 递推公式 子串范围为[i,j],当s[i]s[j]时,有三种情况࿱…...

Element UI框架学习篇(二)
Element UI框架学习篇(二) 1 整体布局 1.1 前提说明 el-container标签里面的标签默认是从左往右排列,若想要从上往下排列,只需要写el-header或者el-footer就行了 <el-container>:外层容器 <el-header>:顶栏容器。 <el-aside>&#…...
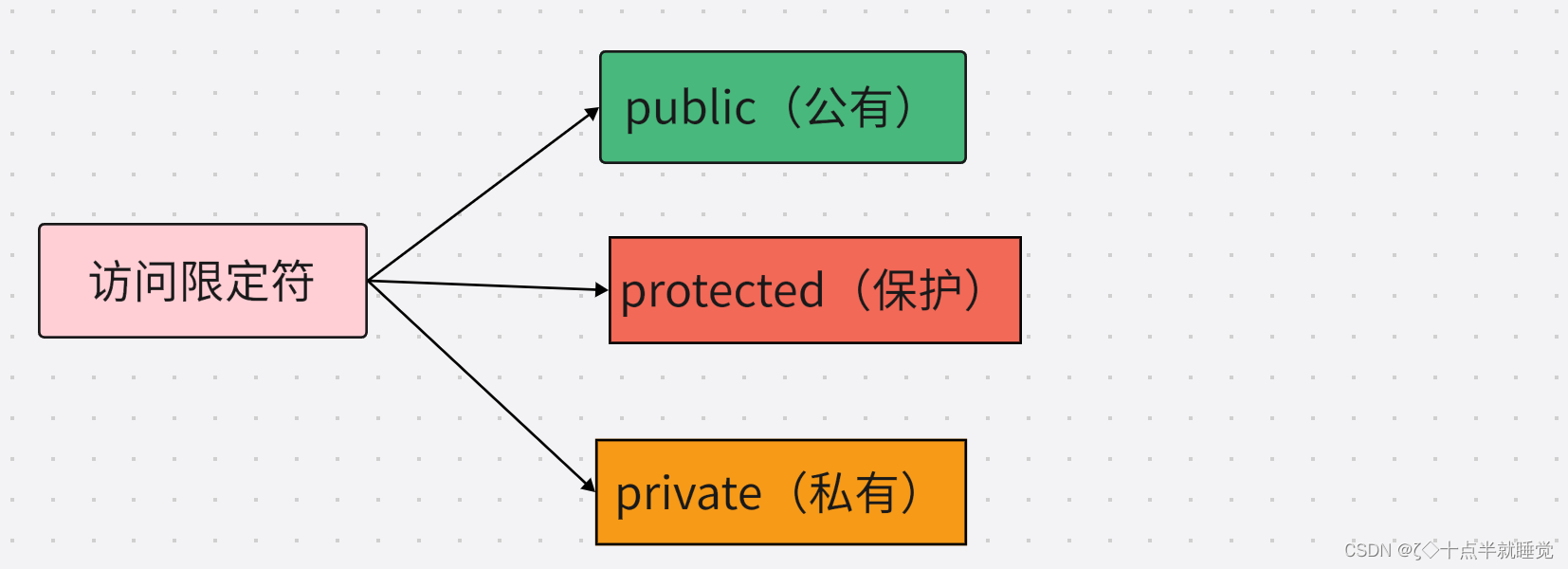
【C++】类与对象(上)
文章目录一、面向过程和面向对象初步认识二、类的引入三、类的定义四、类的访问限定符及封装①访问限定符②封装五、类的作用域六、类的实例化七、类对象模型①如何计算类对象大小②类对象的存储方式③结构体中内存对齐规则八、this指针①this指针的引出②this指针的特性一、面…...
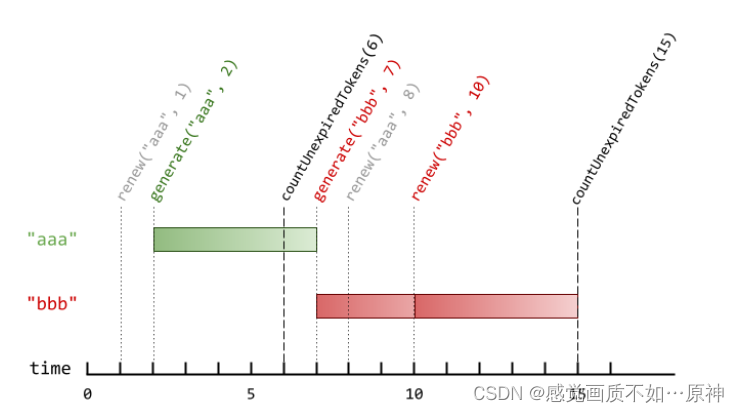
Leetcode.1797 设计一个验证系统
题目链接 Leetcode.1797 设计一个验证系统 Rating : 1534 题目描述 你需要设计一个包含验证码的验证系统。每一次验证中,用户会收到一个新的验证码,这个验证码在 currentTime时刻之后 timeToLive秒过期。如果验证码被更新了,那么它会在 curr…...

Kaldi - 数据文件准备
文章目录数据文件准备wav.scputt2spkspk2utttext相关代码根据文件生成 utt2spk 和 wav.scputt2spk -- spk2utt 转换数据文件准备 在训练/解码中: 有三个文件是必要的: wav.scp 语音编号 – 路径信息utt2spk 语音编号 – 说话人编号spk2utt 说话人编号 …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
