Delaunay三角刨分算法理解及c#过程实现
Delaunay三角刨分算法理解及c#过程实现
- 0 引言
- 1 关于三角剖分
- 2 Delaunay三角剖分算法实现及对比
- 3 结语

0 引言
💻💻AI一下💻💻
三角剖分是什么?
三角剖分是一种将平面或曲面划分成三角形集合的方法。在二维平面中,给定一个平面区域(可以是多边形等),通过连接区域内的一些点,使得整个区域被分割成若干个三角形,这些三角形彼此相邻,且它们的并集就是原来的平面区域。例如,对于一个简单的矩形,我们可以通过连接矩形的对角线,将其三角剖分成两个三角形。
三角剖分需满足的原则?
-
空外接圆原则(Empty - Circumcircle Criterion)
这是 Delaunay 三角剖分最核心的原则。对于任意一个三角形,其外接圆内不包含点集中的其他点。也就是说,如果存在一个点在某个三角形的外接圆内部,那么这个三角形就不符合 Delaunay 三角剖分的要求。
例如,假设有点 A、B、C 构成一个三角形,其外接圆为圆 O。如果在圆 O 内部存在点 D(这个点属于要进行三角剖分的点集),那么三角形 ABC 就需要重新调整,可能会通过连接 AD、BD 或 CD 等来改变三角剖分的结构,以满足外接圆内不包含其他点的条件。 -
最大最小角原则(Max - Min Angle Criterion)
Delaunay 三角剖分在所有可能的三角剖分中,能够使三角形的最小角达到最大。这一原则使得剖分后的三角形形状相对比较 “规则”,尽量避免出现角度过小(如趋近于 0 度)的三角形,因为狭长的三角形在一些应用中(如有限元分析)可能会导致数值计算的不稳定等问题。
例如,在给定一组点进行三角剖分的过程中,有多种连接方式可以形成不同的三角剖分结果。Delaunay 三角剖分算法会倾向于选择那种使得每个三角形的最小角尽可能大的连接方式。 -
局部优化原则(Local Optimization Procedure,LOP)
在构建三角剖分的过程中,当插入一个新的点或者对已有的三角剖分进行调整时,通常会采用局部优化的方法。具体来说,当一个点被插入到现有的三角剖分中,会检查这个点周围的三角形,通过交换对角线等操作来优化局部的三角剖分结构,使其符合 Delaunay 三角剖分的原则。
例如,在逐步构建三角剖分的过程中,新插入一个点 P 后,它周围可能会形成一些新的三角形。这时,会检查这些三角形及其相邻三角形的外接圆情况,如果发现有不符合空外接圆原则的三角形,就会在局部进行调整,比如交换某些三角形的边,直到满足 Delaunay 三角剖分的要求。
本篇基于网络资料,对Delaunay三角剖分算法原理进行理解,并借鉴多篇优秀博文,对算法进行了实现,结果与Matlab内置函数进行比对,边缘存在划分差异,可以 满足实际需要。
1 关于三角剖分
关于Delaunay三角剖分的算法网上有大量博文在介绍相关原理,这里不再展开。但在使用网上获得的各种Delaunay三角剖分算法的时候需要仔细斟酌,因为尝试了许多能下载到的代码,运行结果或多或少都有一些问题。下面是实现三角剖分的几个关键步骤。
(1)构造一个超级三角形,包含所有散点,放入三角形链表;
(2)将点集中的散点依次插入,在三角形链表中找出其外接圆包含插入点的三角形,删除影响三角形的公共边,将插入点同影响三角形的全部顶点连接起来;
(3)根据优化准则对局部新形成的三角形进行优化,将形成的三角形放入 Delaunay 三角形链表;
(4)循环执行上述步骤,直到所有散点插入完毕。
2 Delaunay三角剖分算法实现及对比
本篇参考、使用的程序来自网站,网站主页如下图,浏览网站发现里边不仅有C#版本的triangulate源码,还有c、c++、Fortran、Java等版本的三角刨分源码,基于实际用途尝试运行了其中的一些程序,发现个别程序运行结果效果不好。本篇选择使用下图框选区域的程序进行三角刨分,该程序运行效率高、结果也相对准确,大多情况下与Matlab结果基本一致,但是受数据精度影响较大,可能会出现划分错误的情况,使用过程需注意。


用相同的随机二维散点数据,分别代入Matlab程序和上述C#程序,比较c#程序计算结果是否准确。下面是调用Matlab自带算法进行三角抛分的简单过程:
point = rand(1000,2);
figure
T = delaunay(point);
triplot(T,point(:,1),point(:,2))
以下是C#版本的三角刨分算法调用过程,C#源码中使用程序仅支持整数类型的坐标点,下面分享的方法是对源码进行的改造,可以支持实数类型的散点进行三角划分,下面仅为定义和关键过程。
## 测试代码,用于驱动计算过程
private void button1_Click(object sender, EventArgs e){Vertex.Clear();Triangle.Clear();// 计算前先释放Graphics g1 = pictureBox2.CreateGraphics();g1.Clear(Color.White);pictureBox2.BackColor = Color.White;string[] lines = File.ReadAllLines(@"basepoint.txt");int N = lines.Length;dVertex tnum;for (int i = 1; i <= N; i++){string line = lines[i - 1];// 拆分行string[] v = line.Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);tnum.x = double.Parse(v[0]);tnum.y = double.Parse(v[1]);tnum.z = 0.0;Vertex.Add(tnum);}int tPoints = N;HowMany = 0;HowMany = Triangulate(ref Vertex, ref Triangle);// 绘图Graphics g;g = pictureBox2.CreateGraphics();this.Show();g.CompositingMode = CompositingMode.SourceOver;g.SmoothingMode = SmoothingMode.None;Pen myPen = new Pen(Color.Blue, 1);for (int i = 0; i <= HowMany - 1; i++){double x1 = Vertex[Triangle[i].vv0].x * pictureBox2.Size.Width;double y1 = Vertex[Triangle[i].vv0].y * pictureBox2.Size.Height;double x2 = Vertex[Triangle[i].vv1].x * pictureBox2.Size.Width;double y2 = Vertex[Triangle[i].vv1].y * pictureBox2.Size.Height;double x3 = Vertex[Triangle[i].vv2].x * pictureBox2.Size.Width;double y3 = Vertex[Triangle[i].vv2].y * pictureBox2.Size.Height;g.DrawLine(myPen, (float)x1, (float)y1, (float)x2, (float)y2);g.DrawLine(myPen, (float)x2, (float)y2, (float)x3, (float)y3相关文章:

Delaunay三角刨分算法理解及c#过程实现
Delaunay三角刨分算法理解及c#过程实现 0 引言1 关于三角剖分2 Delaunay三角剖分算法实现及对比3 结语0 引言 💻💻AI一下💻💻 三角剖分是什么? 三角剖分是一种将平面或曲面划分成三角形集合的方法。在二维平面中,给定一个平面区域(可以是多边形等),通过连接区域…...
)
Backend - ADO.NET(C# 操作Oracle、PostgreSQL DB)
目录 一、引入参考 1. ConfigurationManager的调用前提: 2. NpgsqlConnection的调用前提: 3. OracleConnection的调用前提: 二、设置数据库链接字串 1. 在App.config中设定链接数据库详情 2. 获取数据库链接字串 三、调用 1.调用Oracle数据库…...

Idea-离线安装SonarLint插件地址
地址: SonarQube for IDE - IntelliJ IDEs Plugin | Marketplace 选择Install Plugin from Disk..,选中下载好的插件,然后重启idea...

Leetcode Hot100 第三题 234. 回文链表
用快慢指针找到链表中间节点反转后面一段链表遍历每个节点做判断为什么是while pre: 不能写while head呢 ? 答:因为slow节点在反转后,他的前序节点除了反转之后的节点,之前正序的节点仍然存在的,即slow.pre 的next依旧是slow, 我…...

Python教程丨Python环境搭建 (含IDE安装)——保姆级教程!
工欲善其事,必先利其器。 学习Python的第一步不要再加收藏夹了!提高执行力,先给自己装好Python。 1. Python 下载 1.1. 下载安装包 既然要下载Python,我们直接进入python官网下载即可 Python 官网:Welcome to Pyt…...

SpringBoot项目实战(39)--Beetl网页HTML文件中静态图片及CSS、JS文件的引用和展示
使用Beetl开发网页时,在网页中使用的CSS、JS、图片等静态资源需要进行适当的配置才可以展示。大致的过程如下: (1)首先Spring Security框架需要允许js、css、图片资源免授权访问。 (2)网站开发时࿰…...
 算法详解与PyTorch实现)
ARIMA模型 (AutoRegressive Integrated Moving Average) 算法详解与PyTorch实现
ARIMA模型 (AutoRegressive Integrated Moving Average) 算法详解与PyTorch实现 目录 ARIMA模型 (AutoRegressive Integrated Moving Average) 算法详解与PyTorch实现1. ARIMA模型概述1.1 时间序列预测1.2 ARIMA的优势2. ARIMA的核心技术2.1 自回归 (AR)2.2 差分 (I)2.3 移动平…...

【Uniapp-Vue3】swiper滑块视图容器的用法
我们使用swiper标签就可以实现轮播图的效果。 一、swiper组件的结构 整体的轮播图使用swiper标签,轮播的每一页使用swiper-item标签。 <template><swiper class"swiper"><swiper-item><view class"swiper-item">111…...

allure报告修改默认语言为中文
1、项目根目录创建.py文件,把代码复制进去 import os from pathlib import Pathdef create_settings_js_file(directory"../pytest_mytt/reports/allures/", filenamesettings.js):# 创建或确认目录存在Path(directory).mkdir(parentsTrue, exist_okTrue…...

国产3D CAD将逐步取代国外软件
在工业软件的关键领域,计算机辅助设计(CAD)软件对于制造业的重要性不言而喻。近年来,国产 CAD 的发展态势迅猛,展现出巨大的潜力与机遇,正逐步改变着 CAD 市场长期由国外软件主导的格局。 国产CAD发展现状 …...

GolangWeb开发- net/http模块
文章目录 Golang开发-案例整理汇总一、net/http介绍二、HTTP客户端Get请求Post请求三、HTTP服务端总结Golang开发经典案例,点击下方链接 Golang开发-案例整理汇总 一、net/http介绍 Go语言内置的net/http包提供了HTTP客户端和服务端的实现。 文档链接: https://pkg.go.dev/n…...

Vue2中使用Echarts
1.安装echarts 在项目根目录下,使用npm或yarn安装ECharts: npm install echarts --save 或者 yarn add echarts 2.在相应的vue页面中引入echarts <script> import * as echarts from "echarts"; </script> 3.代码解析 <…...

AI赋能服装零售:商品计划智能化,化危机为转机
在服装零售这片竞争激烈的战场上,每一个细微的决策都可能成为品牌兴衰的关键。当市场波动、消费者口味变化、供应链挑战接踵而至时,许多品牌往往将危机归咎于外部环境。然而,真相往往更为深刻——“危机不是外部的,而是你的商品计…...

Spring AI ectorStore
Spring AI中的VectorStore是一种用于存储和检索高维向量数据的数据库或存储解决方案,它在AI应用中扮演着至关重要的角色。以下是对Spring AI VectorStore的详细解析: 一、VectorStore的基本概念 定义:VectorStore特别适用于处理那些经过嵌入…...

zig 安装,Hello World 示例
1. 安装 Zig 首先,你需要在你的计算机上安装 Zig 编译器。你可以从 Zig 官方网站 下载适合你操作系统的版本。 安装完成后,你可以在终端中运行以下命令来检查 Zig 是否安装成功: zig version如果一切正常,它会显示 Zig 的版本信…...

龙蜥Linux系统部署docker21.1.3版本
龙蜥系统配置docker环境 更新yum源 更新软件源中的包。 yum update安装底层工具 yum install -y yum-utils device-mapper-persistent-data lvm2添加阿里云仓库 # 添加阿里云的docker镜像仓库 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/c…...

django解决跨域问题
# 1.安装django-cors-headers 库 pip install django-cors-headers -i https://pypi.tuna.tsinghua.edu.cn/simple2.添加到应用程序中 添加 corsheaders 到你的 INSTALLED_APPS 设置中: INSTALLED_APPS [...corsheaders,... ]3.添加中间件 MIDDLEWARE [...cor…...

【蓝桥杯选拔赛真题60】C++寻宝石 第十四届蓝桥杯青少年创意编程大赛 算法思维 C++编程选拔赛真题解
目录 C++寻宝石 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 五、运行结果 六、考点分析 七、推荐资料 C++寻宝石 第十四届蓝桥杯青少年创意编程大赛C++选拔赛真题 一、题目要求 1、编程实现 有N(1<N<100)个盒子排成一排,每个盒子都放…...

Git 从入门到精通
一、环境配置 下载地址:https://git-scm.com/downloads/ 二、用户配置 找到git bash git --version 查看当前版本 git config --global user.name szhipeng625 设置用户名 git config --global user.email szhipeng625gmail.com 设置邮箱 git config --global …...

vue3使用vue3-video-play播放m3u8视频
1.安装vue3-video-play npm install vue3-video-play --save2.在组件中使用 import vue3-video-play/dist/style.css; import VideoPlay from vue3-video-play;// 视频配置项 const options reactive({src: https://test-streams.mux.dev/x36xhzz/x36xhzz.m3u8, //视频源mute…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...
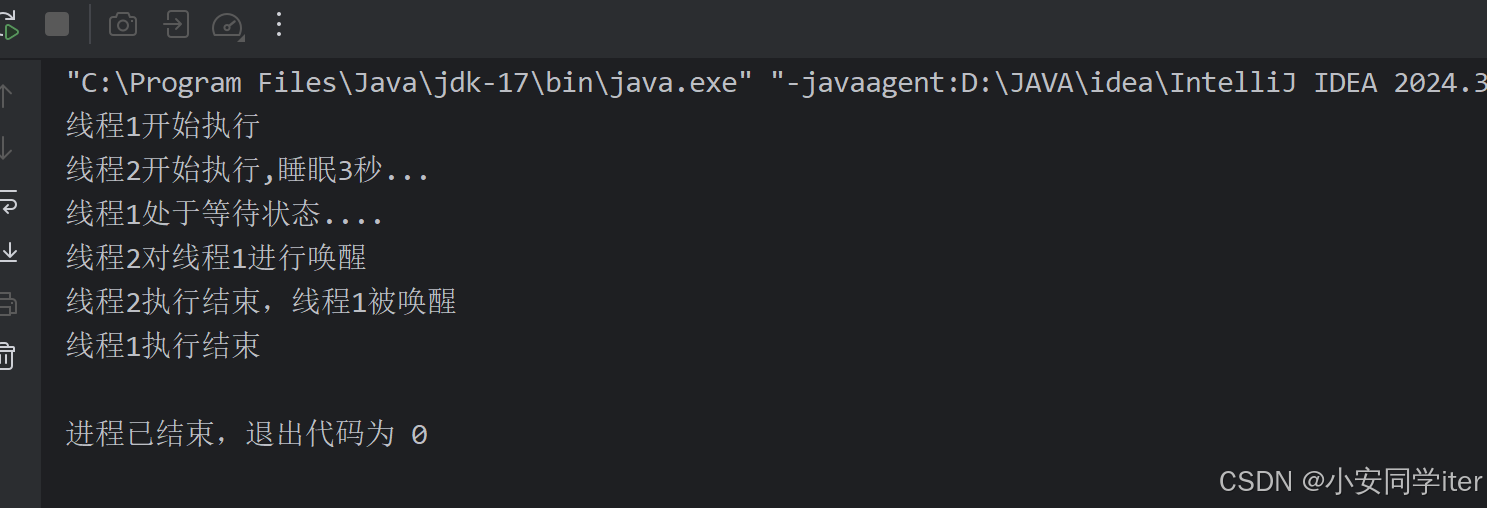
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...

十二、【ESP32全栈开发指南: IDF开发环境下cJSON使用】
一、JSON简介 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,具有以下核心特性: 完全独立于编程语言的文本格式易于人阅读和编写易于机器解析和生成基于ECMAScript标准子集 1.1 JSON语法规则 {"name"…...
