数据结构二叉树-C语言
数据结构二叉树-C语言
- 1.树
- 1.1树的概念与结构
- 1.2树的相关术语
- 1.3树的表示
- 1.4树形结构实际运用场景
- 2.二叉树
- 2.1概念与结构
- 2.2特殊的二叉树
- 2.2.1满二叉树
- 2.2.2完全二叉树
- 2.3二叉树存储结构
- 2.3.1顺序结构
- 2.3.2链式结构
- 3.实现顺序结构的二叉树
- 4.实现链式结构二叉树
- 4.1前中后序遍历
- 4.1.1遍历规则
- 4.1.2代码实现
- 4.2结点个数以及高度等
1.树
1.1树的概念与结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树,也就是说它是根朝上,而叶朝下的。
•有一个特殊的结点,称为根结点,根结点没有前驱结点。
•除根结点外,其余结点被分为M(M>0)个互不相交的集合T1、T2、…Tm,其中每一个集合Ti(1<=i<=m)又是一颗结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。因此,树是递归定义的。
如图1所示:

树形结构中,子树之间不能有交集,否则就不是树形结构
非树形结构:

•子树是不相交的(如果存在相交就是图了)
•除了根结点外,每个结点有且仅有一个父结点
•一颗N个结点的树有N-1条边
1.2树的相关术语
根据图1:
夫结点/双亲结点:若一个结点含有子结点,则这个结点称为其子结点的夫结点;如图1A是B的夫结点。
子结点/孩子结点:一个结点含有子树的根节点称为该结点的子结点;如图1B是A的孩子结点。
结点的度:一个结点有几个孩子,他的度就是多少;比如A的度为2,D的度为1.
树的度:一棵树中,最大的结点的度称为树的度;如图1,最大的度为2
叶子结点/终端结点:度为0的结点称为叶节点;如图1,H、E、F、G为叶子结点。
分支结点/非终端结点:度不为0的结点;如图1中的D、B、C为分支结点。
兄弟结点:具有相同父结点的结点互称为兄弟结点(亲兄弟);如图1中的B和C是兄弟结点。
结点的层次:从根开始定义起,根为第一层,根的子结点为第二层,依次类推。
树的高度或深度:树中结点的最大层次;如图1:树的高度为4.
结点的祖先:从根到该结点所经分支上的所有结点;如图1:A是所有结点的祖先。
路径:一条从树中任意结点出发,沿父节点-子结点连接,达到任意结点的序列;比如A到H的路径为A-B-D-H,从A到F的路径为A-C-F。
子孙:以某结点为根的子树中任一结点的子孙。如图1:所有结点都是A的子孙。
森林:由m(m>0)课互不相交的树称为森林。
1.3树的表示
既要保存值域,也要保存结点和结点之间的关系。
使用孩子兄弟表示法。
1.4树形结构实际运用场景
文件系统是计算机存储和管理文件的一种方式,它利用树形结构来组织和管理文件和文件夹。在文件系统中,树结构被广泛应用,它通过夫结点和子结点之间的关系来表示不同层级的文件和文件夹之间的关联。
2.二叉树
2.1概念与结构
在树结构中,我们最常用的就是二叉树,一颗二叉树是结点的一个有限集合,该集合由一个根结点加上两课别称为左子树和右子树的二叉树组成或者为空。

从图上可以看出二叉树具有以下特点:
1.二叉树不存在度大于2的结点
2.二叉树的子树有左右之分,依序不能颠倒,因此二叉树是有序树。
注意:对于任意的二叉树都是由以下几种情况复合而成的。

2.2特殊的二叉树
2.2.1满二叉树
一个二叉树,如果每一个层的结点树都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为k,且结点总数是2^k-1,则它就是满二叉树。

2.2.2完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

二叉树性质:
根据满二叉树的特点可知:
1)若规定根结点的层数为1,则一颗非空二叉树的第i层上最多有2^(i-1)
2)若规定根结点的层数为1,则深度为h的二叉树的最大结点数是2^h-1.
3)若规定根结点的层数为1,具有n个结点的满二叉树的深度h=log2(n+1)(log以2为底,n+1为对数)
2.3二叉树存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
2.3.1顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费,完全二叉树更适合使用顺序结构存储。


现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
2.3.2链式结构
二叉树的链式存储结构是值,用链表来表示一颗二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链。


3.实现顺序结构的二叉树
一般使用顺序结构的数组来存储数据,堆是一种特殊的二叉树,具有二叉树的特性的同时,还具备其他的特性。(通过堆来实现)下一期内容写堆
4.实现链式结构二叉树
用链表来表示一颗二叉树,即 用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出结点左孩子和右孩子所在的链结点的存储地址,其结构如下:
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;//当前结点的数据域struct BinaryTreeNode* _left;//指向当前结点左孩子struct BinaryTreeNode* _right;//指向当前结点的右孩子
}BTNode;
二叉树的创建方式比较复杂,为了更好的步入到二叉树内容中,手动创造一课链式二叉树
//手动构造树
BTNode* CreateTree()
{BTNode* nodeA = buyNode('A');BTNode* nodeB = buyNode('B');BTNode* nodeC = buyNode('C');BTNode* nodeD = buyNode('D');BTNode* nodeE = buyNode('E');BTNode* nodeF = buyNode('F');nodeA->_left = nodeB;nodeA->_right = nodeC;nodeB->_left = nodeD;nodeC->_left = nodeE;nodeC->_right = nodeF;return nodeA;
}
二叉树分为空树和非空二叉树由根结点、根结点的左孩子、根结点的右孩子组成的。

根结点的左子树和右子树分别又是由子树结点、子树结点的左孩子、子树结点的右孩子组成的,因此二叉树定义是递归式的,后序链式二叉树的操作中基本都是按照该概念实现的。
4.1前中后序遍历
二叉树的操作离不开树的遍历,我们先来看看二叉树的遍历有哪些方式

4.1.1遍历规则
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1)前序遍历:访问根结点的操作发生在遍历其左右子树之前
访问顺序为:根结点、左子树、右子树
2)中序遍历:访问根结点的操作发生在遍历其左右子树之中(间)
访问顺序为:左子树、根结点、右子树
3)后序遍历:访问根结点的操作发生在遍历其左右子树之后
访问顺序为:左子树、右子树、根结点
4.1.2代码实现
//先序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}//中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}BinaryTreeInOrder(root->_left);printf("%c ", root->_data);BinaryTreeInOrder(root->_right);
}//后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c ", root->_data);
}
图解遍历:
以前序遍历为例:

4.2结点个数以及高度等
头文件:
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
.c文件
//先序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
先序遍历遵循根左右的原则,使用递归的方法,先将根结点打印出来,在访问结点的左孩子,直到访问到为空,在回到结点,访问结点的右孩子。
//中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}BinaryTreeInOrder(root->_left);printf("%c ", root->_data);BinaryTreeInOrder(root->_right);
}中序遍历遵循左根右的原则,在进行递归的方式进行遍历左孩子,并将根结点打印访问,再遍历结点的右孩子。
//后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c ", root->_data);
}
如上规律。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;//return直接跳出,return 0是返回的是0.}return 1 + BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right);
}
二叉树结点的个数等=根结点+左孩子的个数+右孩子的个数
通过递归访问将每个结点的左孩子和右孩子加起来,最后就能算出二叉树节点的个数。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;//左节点和右节点都必须满足为空的情况下,直接返回1,说明二叉树中只有根结点,没有其他子结点。}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
二叉树中的叶子结点=左孩子的叶子节点+右孩子的叶子结点。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)//当k等于0的时候就不会进函数了。
{if (root == NULL){return 0;}if (k == 1){return 1;//如果k=1的时候,就只有根结点,第一层也就只有一个结点。}return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
给该函数传入两个参数,一个是根结点,一个是第k层,从根结点开始向下遍历,每遍历一次k就-1,直到k为0时,就不再进函数,直接返回。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->_data = x){return root;}BTNode* leftFind = BinaryTreeFind(root->_left, x);if (leftFind){return root;}BTNode* rightFind = BinaryTreeFind(root->_right, x);if (rightFind){return rightFind;}return NULL;//如果到这里了,就是没找到。
}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)//因为需要改变原本的值,所以需要传二级指针
{if (*root == NULL){return;}BinaryTreeDestory(&((*root)->_left));BinaryTreeDestory(&((*root)->_right));free(*root);*root == NULL;
}
相关文章:

数据结构二叉树-C语言
数据结构二叉树-C语言 1.树1.1树的概念与结构1.2树的相关术语1.3树的表示1.4树形结构实际运用场景 2.二叉树2.1概念与结构2.2特殊的二叉树2.2.1满二叉树2.2.2完全二叉树 2.3二叉树存储结构2.3.1顺序结构2.3.2链式结构 3.实现顺序结构的二叉树4.实现链式结构二叉树4.1前中后序遍…...

Python基于YOLOv8和OpenCV实现车道线和车辆检测
使用YOLOv8(You Only Look Once)和OpenCV实现车道线和车辆检测,目标是创建一个可以检测道路上的车道并识别车辆的系统,并估计它们与摄像头的距离。该项目结合了计算机视觉技术和深度学习物体检测。 1、系统主要功能 车道检测&am…...

代码随想录算法训练营第六十天|KM94.城市间货物运输Ⅰ|KM95.城市间货物运输Ⅱ|KM96.城市间货物运输Ⅲ
94. 城市间货物运输 I 2、Bellman_ford队列优化算法(又名SPFA) SPFA是对Bellman_ford算法的优化,由于Bellman_ford 算法 每次都是对所有边进行松弛,其实是多做了一些无用功。其实只需要对 上一次松弛的时候更新过的节点作为出发节…...

人工智能学习路线全链路解析
一、基础准备阶段(预计 2-3 个月) (一)数学知识巩固与深化 线性代数(约 1 个月): 矩阵基础:回顾矩阵的定义、表示方法、矩阵的基本运算(加法、减法、乘法)&…...

C++语言的学习路线
C语言的学习路线 C是一种强大的高级编程语言,广泛应用于系统软件、游戏开发、嵌入式系统和高性能应用等多个领域。由于其丰富的功能和灵活性,C是一门值得深入学习的语言。本文旨在为初学者制定一条系统的学习路线,帮助他们循序渐进地掌握C语…...
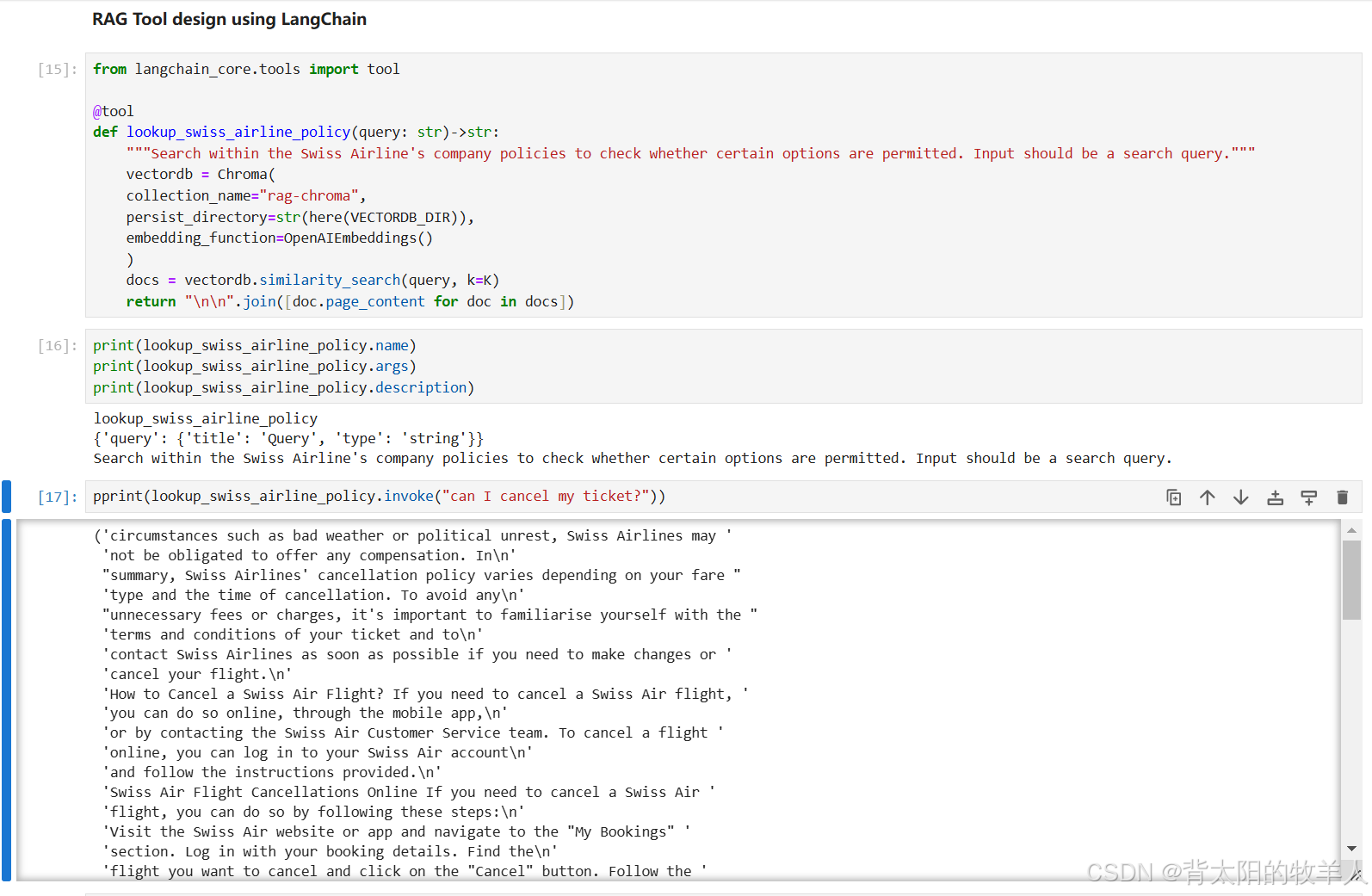
用于与多个数据库聊天的智能 SQL 代理问答和 RAG 系统(3) —— 基于 LangChain 框架的文档检索与问答功能以及RAG Tool的使用
介绍基于 LangChain 框架的文档检索与问答功能,目标是通过查询存储的向量数据库(VectorDB),为用户的问题检索相关内容,并生成自然语言的答案。以下是代码逻辑的详细解析: 代码结构与功能 初始化环境与加载…...
20250110doker学习记录
1.本机创建tts环境。用conda. 0.1安装。我都用的默认,你也可以。我安装过一次,如果修复,后面加 -u bash Anaconda3-2024.10-1-Linux-x86_64.sh等待一会。 (base) ktkt4028:~/Downloads$ conda -V conda 24.9.2学习资源 Conda 常用命令大…...

MPU6050: 卡尔曼滤波, 低通滤波
对于MPU6050(一种集成了三轴加速度计和三轴陀螺仪的惯性测量单元),对加速度值进行卡尔曼滤波,而对角速度进行低通滤波的选择是基于这两种传感器数据的不同特性和应用需求。以下是详细解释: 加速度值与卡尔曼滤波 为什么使用卡尔曼滤波? 噪声抑制: 加速度计信号通常包含…...

C++的标准和C++的编译版本
C的标准和C的编译版本:原理和概念 理解 C标准 和 C编译版本 的关系是学习 C 的一个重要部分。这两者虽然看似相关,但实际上分别涉及了不同的概念和技术。下面将通过层次清晰的解释,帮助新手理解这两个概念的差异、特点及其相互关系。 一、C标…...
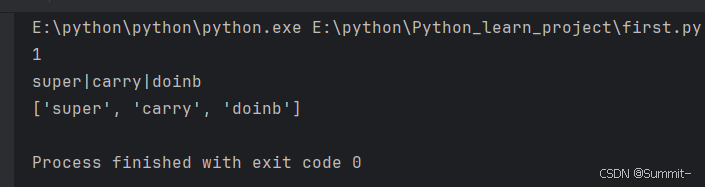
python学习笔记—17—数据容器之字符串
1. 字符串 (1) 字符串能通过下标索引来获取其中的元素 (2) 旧字符串无法修改特定下标的元素 (3) index——查找字符串中任意元素在整个字符串中的起始位置(单个字符或字符串都可以) tmp_str "supercarrydoinb" tmp_position1 tmp_str.index("s") tmp_p…...
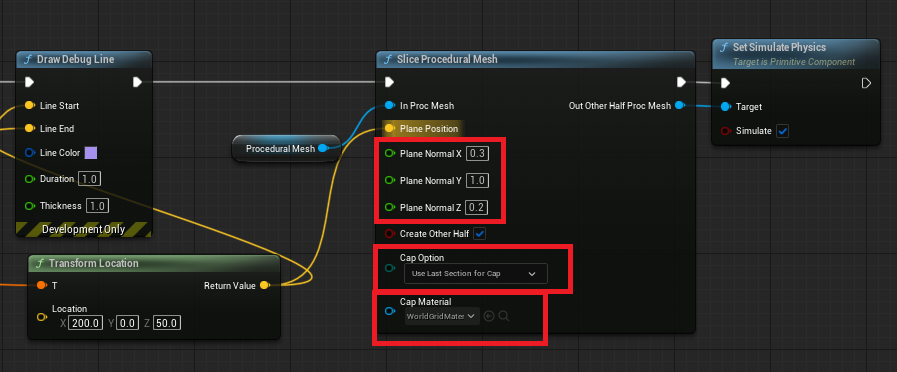
UE5 使用内置组件进行网格切割
UE引擎非常强大,直接内置了网格切割功能并封装为蓝图节点,这项功能在UE4中就存在,并且无需使用Chaos等模块。那么就来学习下如何使用内置组件实现网格切割。 1.配置测试用StaticMesh 对于被切割的模型,需要配置一些参数。以UE5…...
51单片机——串口通信(重点)
1、通信 通信的方式可以分为多种,按照数据传送方式可分为串行通信和并行通信; 按照通信的数据同步方式,可分为异步通信和同步通信; 按照数据的传输方向又可分为单工、半双工和全双工通信 1.1 通信速率 衡量通信性能的一个非常…...

Taro+Vue实现图片裁剪组件
cropper-image-taro-vue3 组件库 介绍 cropper-image-taro-vue3 是一个基于 Vue 3 和 Taro 开发的裁剪工具组件,支持图片裁剪、裁剪框拖动、缩放和输出裁剪后的图片。该组件适用于 Vue 3 和 Taro 环境,可以在网页、小程序等平台中使用。 源码 https:…...
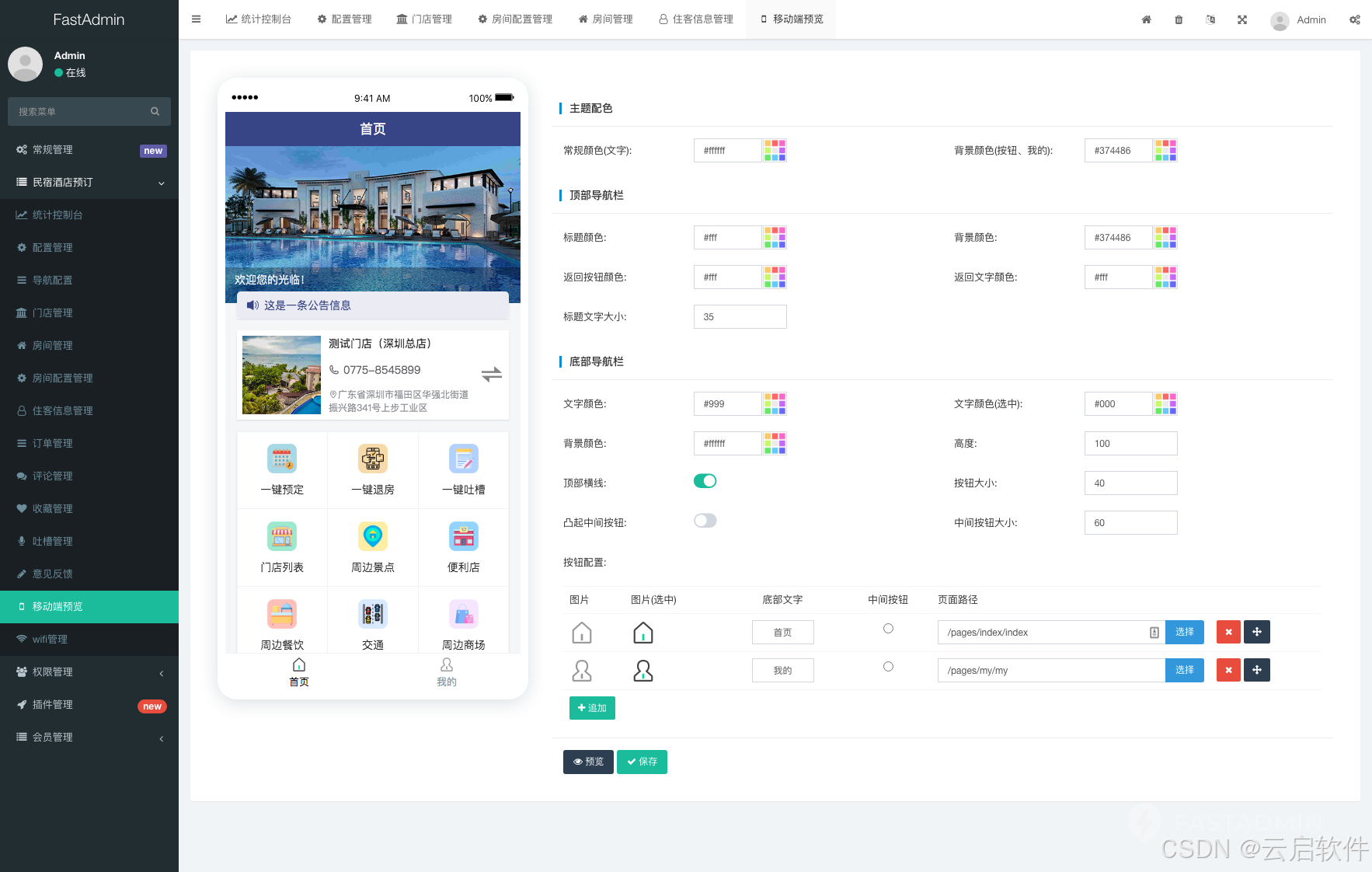
PHP民宿酒店预订系统小程序源码
🏡民宿酒店预订系统 基于ThinkPHPuniappuView框架精心构建的多门店民宿酒店预订管理系统,能够迅速为您搭建起专属的、功能全面且操作便捷的民宿酒店预订小程序。 该系统不仅涵盖了预订、退房、WIFI连接、用户反馈、周边信息展示等核心功能,更…...
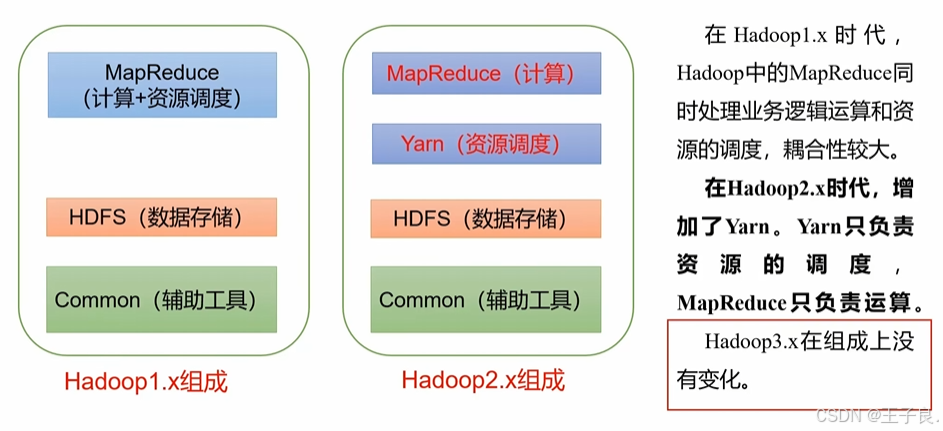
Hadoop3.x 万字解析,从入门到剖析源码
💖 欢迎来到我的博客! 非常高兴能在这里与您相遇。在这里,您不仅能获得有趣的技术分享,还能感受到轻松愉快的氛围。无论您是编程新手,还是资深开发者,都能在这里找到属于您的知识宝藏,学习和成长…...

VUE3 常用的组件介绍
Vue 组件简介 Vue 组件是构建 Vue 应用程序的核心部分,组件帮助我们将 UI 分解为独立的、可复用的块,每个组件都有自己的状态和行为。Vue 组件通常由模板、脚本和样式组成。组件的脚本部分包含了各种配置选项,用于定义组件的逻辑和功能。 组…...

deepin-Wine 运行器合并打包器和添加从镜像提取 DLL 的功能
Wine 运行器是一个图形化工具,旨在简化 Wine 环境的管理和使用。它不仅提供了运行和管理 Wine 容器的功能,还增加了打包器和从镜像提取 DLL 的功能。以下是该工具的详细介绍和使用方法。 一、工具概述 Wine 运行器是一个使用 Python3 的 tkinter 构建的图…...

[大模型]本地离线运行openwebui+ollama容器化部署
本地离线运行Openweb-ui ollama容器化部署 说明安装internet操作内网操作问题线程启动错误最终命令总结说明 最近公司有一个在内网部署一个离线大模型的需求,网络是离线状态,服务器有A100GPU,一开始是想折腾开源chatGML4大模型,因为使用过gml3,所以想着部署gml4应该不难。…...
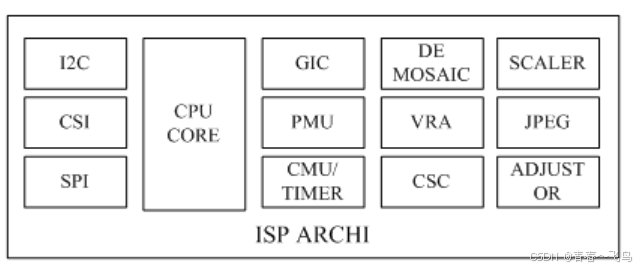
再次梳理ISP的大致流程
前言: 随着智能手机的普及,相机与我们的生活越来越紧密相关。在日常生活中,我们只需要轻轻按下手机上的拍照按钮,就能记录下美好时刻。那么问题来了:从我们指尖按下拍照按钮到一张色彩丰富的照片呈现在我们面前&#x…...
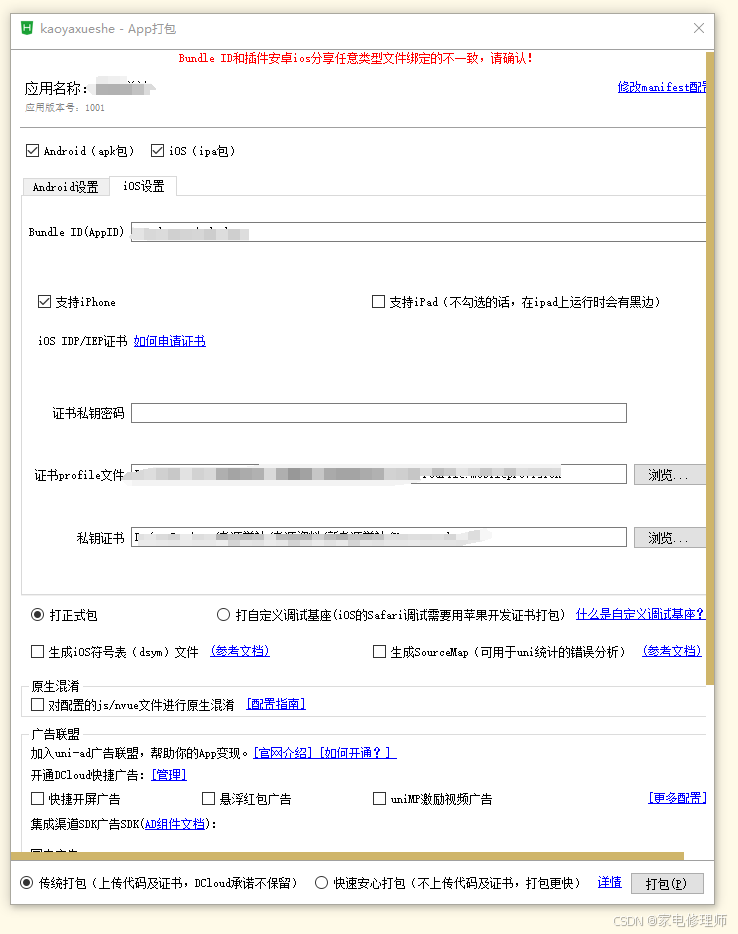
HBuilderX打包ios保姆式教程
1、登录苹果开发者后台并登录已认证开发者账号ID Sign In - Apple 2、创建标识符(App ID)、证书,描述文件 3、首先创建标识符,用于新建App应用 3-1、App的话直接选择第一个App IDs,点击右上角继续 3-2、选择App&#x…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
