机器学习(1):线性回归概念
1 线性回归基础
1.1 什么是线性
例如:汽车每小时60KM,3小时可以行使多长距离?已知汽车的速度,则汽车的行使距离只与时间唯一相关。在二元的直角坐标系中,描出这一关系的图是一条直线,所以称为线性关系。
线性特点是一个事物唯一由另一个事物决定。
1.2 什么是回归
那么,这个回归究竟是什么意思呢?其实回归算法是相对分类算法而言的,与我们想要预测的目标变量y的值类型有关。如果目标变量y是分类型变量,如预测用户的性别(男、女),预测月季花的颜色(红、白、黄……),预测是否患有肺癌(是、否),那我们就需要用分类算法去拟合训练数据并做出预测;如果y是连续型变量,如预测用户的收入(4千,2万,10万……),预测员工的通勤距离(500m,1km,2万里……),预测患肺癌的概率(1%,50%,99%……),我们则需要用回归模型。
有时分类问题也可以转化为回归问题,例如刚刚举例的肺癌预测,我们可以用回归模型先预测出患肺癌的概率,然后再给定一个阈值,例如50%,概率值在50%以下的人划为没有肺癌,50%以上则认为患有肺癌。这种分类型问题的回归算法预测,最常用的就是逻辑回归,后面我们会讲到。
2 一元线性回归
线性回归可以说是用法非常简单、用处非常广泛、含义也非常容易理解的一类算法,作为机器学习的入门算法非常合适。我们上中学的时候,都学过二元一次方程,我们将y作为因变量,x作为自变量,得到方程:
y=β0+β1x
当给定参数β0和β1的时候,画在坐标图内是一条直线(这就是“线性”的含义)。当我们只用一个x来预测y,就是一元线性回归,也就是在找一个直线来拟合数据。比如,我有一组数据画出来的散点图,横坐标代表广告投入金额,纵坐标代表销售量,线性回归就是要找一条直线,并且让这条直线尽可能地拟合图中的数据点。

这里我们得到的拟合方程是y = 0.0512x + 7.1884,此时当我们获得一个新的广告投入金额后,我们就可以用这个方程预测出大概的销售量。
数学理论的世界是精确的,譬如你代入x=0就能得到唯一的 y^ ,y^=7.1884(y上面加一个小帽子hat,表示这个y^不是我们真实观测到的,而是估计值)。但现实世界中的数据就像这个散点图,我们只能尽可能地在杂乱中寻找规律。用数学的模型去拟合现实的数据,这就是统计。统计不像数学那么精确,统计的世界不是非黑即白的,它有“灰色地带”,但是统计会将理论与实际间的差别表示出来,也就是“误差”。因此,统计世界中的公式会有一个小尾巴 μ ,用来代表误差,即:
y=β0+β1x+μ
3.损失函数
那既然是用直线拟合散点,为什么最终得到的直线是y = 0.0512x + 7.1884,而不是下图中的y = 0.0624x + 5呢?这两条线看起来都可以拟合这些数据啊?毕竟数据不是真的落在一条直线上,而是分布在直线周围,所以我们要找到一个评判标准,用于评价哪条直线才是最“合适”的。

我们先从残差说起。残差说白了就是真实值和预测值间的差值(也可以理解为差距、距离),用公式表示是:
e=y−y^

对于某个广告投入 xi ,我们有对应的实际销售量 yi ,和预测出来的销售量yi^(音:yihat)(通过将xi代入公式y=β0+β1x计算得到),计算 ei=yi−y^i 的值,再将其平方(为了消除负号),对于我们数据中的每个点如此计算一遍,再将所有的 ei2相加,就能量化出拟合的直线和实际之间的误差。用公式表示就是:
Q=∑1n(yi−y^i)2=∑1n(yi−(β^0+β^1xi))2
这个公式是残差平方和,即SSE(Sum of Squares for Error),在机器学习中它是回归问题中最常用的损失函数。
现在我们知道了损失函数是衡量回归模型误差的函数,也就是我们要的“直线”的评价标准。这个函数的值越小,说明直线越能拟合我们的数据。如果还是觉得难理解,我下面就举个具体的例子。
假设我们有一组样本,建立了一个线性回归模型f(x),
- 样本A:公司投入了x=1000元做广告,销售量为y=60,f(x=1000)算出来是50,有-10的偏差。
- 样本B:x=2000,销售量为y=95,f(x=2000)=100,偏差为5。
- 样本C:x=3000,销售量为y=150,f(x=2000)=150,偏差为0哦,没有偏差
要计算A、B、C的整体偏差,因为有正有负,所以做个平方,都弄成正的,然后再相加,得到总偏差,也就是平方损失,是125。
4 最小二乘法与梯度下降法
4.1 最小二乘法
我们不禁会问,这个β0和β1的具体值究竟是怎么算出来的呢?我们知道,两点确定一线,有两组x,y的值,就能算出来β0和β1。但是现在我们有很多点,且并不正好落在一条直线上,这么多点每两点都能确定一条直线,这到底要怎么确定选哪条直线呢?
当给出两条确定的线,如y = 0.0512x + 7.1884,y = 0.0624x + 5时,我们知道怎么评价这两个中哪一个更好,即用损失函数评价。那么我们试试倒推一下?
给定一组样本观测值xi,yi(i=1,2,…n),要求回归函数尽可能拟合这组值。普通最小二乘法给出的判断标准是:残差平方和的值达到最小。我们再来看一下残差平方和的公式:
Q=∑1n(yi−y^i)2=∑1n(yi−(β^0+β^1xi))2
这个公式是一个二次方程,我们知道一元二次方程差不多长下图这样:

上面公式中 β^0 和 β^1 未知,有两个未知参数的二次方程,画出来是一个三维空间中的图像,类似下面:

还记得微积分知识的话,就知道导数为0时,Q取最小值,因此我们分别对β^0和β^1求偏导并令其为0:
∂Q∂β0=2∑1n(yi−β0^−β1^xi)=0
∂Q∂β1=2∑1n(yi−β0^−β1^xi)xi=0
xi,yi(i=1,2,…n)都是已知的,全部代入上面两个式子,就可求得β^0和β^1的值啦。这就是最小二乘法,“二乘”是平方的意思。
线性回归是对一个或多个自变量之间关系进行建模的方法。以上举的例子是一维的例子(x只有一个),如果有两个特征,就是二元线性回归,要拟合的就是二维空间中的一个平面。如果有多个特征,那就是多元线性回归:
y=β0+β1x1+β2x2+⋯+βpxp
最后再提醒一点,做线性回归,不要忘了前提假设是y和x呈线性关系,如果两者不是线性关系,就要选用其他的模型啦。
4.2 梯度下降法
梯度下降法的基本思想可以类比为一个下山的过程,如下图所示函数看似为一片山林,红色的是山林的高点,蓝色的为山林的低点,蓝色的颜色越深,地理位置越低,则图中有一个低点,一个最低点。

假设这样一个场景:一个人被困在山上(图中红圈的位置),需要从山上下来(找到山的最低点,也就是山谷),但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的方向走,然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。

假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的工具。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率(多久测量一次),来确保下山的方向不错误,同时又不至于耗时太多,在算法中我们成为步长。
按照梯度下降算法的思想,它将按如下操作达到最低点:
- 明确自己现在所处的位置
- 找到相对于该位置而言下降最快的方向
- 沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置肯定比原来低
- 回到第一步
- 终止于最低点
按照以上5步,最终达到最低点,这就是梯度下降的完整流程。当然你可能会说,上图不是有不同的路径吗?是的,因为上图并不是标准的凸函数,往往不能找到最小值,只能找到局部极小值。所以你可以用不同的初始位置进行梯度下降,来寻找更小的极小值点。
4.3 总结
最小二乘法和梯度下降法都是经典的学习算法,在给定已知数据的前提下利用求导算出一个模型(函数),使得损失函数值最小,后对给定的新数据进行估算预测。两者的区别:
- 损失函数不同:梯度下降可以选取其它损失函数;而最小二乘法一定是平方损失函数。
- 实现方法不同:最小二乘法是直接求导找出全局最小;而梯度下降是一种迭代法。
- 效果不同:最小二乘法一定是全局最小,但计算繁琐,且复杂情况下未必有解;梯度下降迭代计算简单,但找到的一般是局部最小,只有在目标函数是凸函数时才是全局最小,到最小点附近收敛速度会变慢,且对初始点的选择极为敏感。
相关文章:

机器学习(1):线性回归概念
1 线性回归基础 1.1 什么是线性 例如:汽车每小时60KM,3小时可以行使多长距离?已知汽车的速度,则汽车的行使距离只与时间唯一相关。在二元的直角坐标系中,描出这一关系的图是一条直线,所以称为线性关系。 线…...

关于编写测试用例的细枝末节
这里写目录标题 故障判别类-边界考虑示例1.0:若A>20.3且持续时间≥15ms时(判故周期为1000Hz),输出B为1,否则输出B为0。 故障判别类-不可恢复测试示例1.1:若A>20.3且持续时间≥15ms时…...

《计算机网络》课后探研题书面报告_了解PPPoE协议
PPPoE协议的工作原理与应用分析 摘 要 PPPoE(Point-to-Point Protocol over Ethernet)是一种广泛应用于宽带接入的网络协议,特别是在DSL(数字用户线路)和光纤网络中具有重要的应用价值。PPPoE结合了PPP协议的认证、加…...

Linux Centos 安装Jenkins到服务
一、前言 假设你已经下载了jenkins.war 安装了对应的jdk,下面我们来安装jenkins,以服务的形式安装。 二、安装 1)将jenkins.war拷贝到合适的位置,我的位置 /u01/jenkins/ ,位置你自己选。 2)创建系统用户…...

解决“无法定位程序输入点 av_buffer_create 于动态链接库 XXX\Obsidian.exe 上”问题
解决“无法定位程序输入点 av_buffer_create 于动态链接库 XXX\Obsidian.exe 上”问题 问题描述 本人在使用zotero中的zotero one(青柠学术插件)的时候,使用插件跳转obsidian中的对应笔记,出现上图情况。(错误中提到的…...

基于考研概率论知识解读 Transformer:为何自注意力机制要除以根号 dk
Transformer自注意力机制中除以 d k \sqrt{d_k} dk 深度剖析 【 Transformer 系列,故事从 d k \sqrt{d_k} dk 说起】 LLM这么火,Transformer厥功甚伟,某天心血来潮~,再去看看! 它长这个样子: 深入…...

网络安全学习81天(记录)
前言: 小迪安全,81天,开始了php代码审计 思路: 内容: #知识点: 1、审计漏洞-SQL 数据库注入挖掘 1、审计思路-正则搜索&功能追踪&辅助工具 3、审计类型-常规架构&MVC 架构&三方框架 #章…...
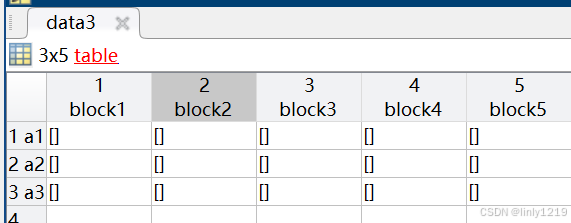
MATLAB学习笔记-table
1.在table中叠加table table 的每一列具有固定的数据类型。如果要让表的所有单元格都可以任意填充,就得让每一列都是 cell 类型,这样表中每个单元格都是“一个元胞”。创建时可以先构造一个 空 cell 数组(大小为行数列数)&#x…...

mybatisPlus(条件构造器API)
文章目录 目录一、mybatisPlus的介绍二、mybatisPlus的基础使用配置BaseMapper的基本CURD(增删改查) 三、wrapper(条件构造器)条件构造器(wrapper)通用API基础条件判断:进阶条件判断(…...

5G+工业互联网迈入规模化发展新阶段
百度安全验证 https://blog.csdn.net/qq_25467441/article/details/145036191?sharetypeblogdetail&sharerId145036191&sharereferPC&sharesourceqq_25467441&spm1011.2480.3001.8118 好看视频-轻松有收获 产业供给加速提升。国内主流模组厂商引领全球5G模组…...

【CI/CD构建】关于不小心将springMVC注解写在service层
背景 之前写一个接口的时候没有察觉到将RequestBody这个注解带到service层了。 今天提交代码的时候,插件没有检测到这个低级错误,导致试飞构建连maven编译都过不了,maven找不到程序包org.springframework.web.bind.annotation这个包 结果…...

《鸿蒙Next ArkTS:开启人工智能应用开发高效新旅程》
在当今科技飞速发展的时代,人工智能与鸿蒙Next的结合正成为开发者们关注的焦点。利用鸿蒙Next的ArkTS语言开发高效的人工智能驱动的应用程序,为我们带来了前所未有的机遇和创新空间。 了解ArkTS语言与鸿蒙Next ArkTS是一种基于TypeScript的静态类型脚本…...

Unity 3D游戏开发从入门进阶到高级
本文精心整理了Unity3D游戏开发相关的学习资料,涵盖入门、进阶、性能优化、面试和书籍等多个维度,旨在为Unity开发者提供全方位、高含金量的学习指南.欢迎收藏。 学习社区 Unity3D开发者 这是一个专注于Unity引擎的开发者社区,汇聚了众多Un…...

什么是SSH登录?SSH客户端软件有哪些?
一、SSH解释 SSH(Secure Shell)登录是一种用于计算机之间加密登录的网络协议。SSH登录允许用户通过互联网访问、控制和修改远程服务器。它提供了加密的通信通道,以保护敏感数据的机密性和完整性。SSH协议支持多种应用,包括SSH&…...

Ubuntu服务器提示:检测到存在恶意文件,补救思路
1. 确定文件类型 可以使用file命令来检查该文件的类型,这有助于判断它是否真的是一个恶意文件 file /path/to/the/file 2. 检查文件内容 使用strings命令查看文件内容,看是否有可疑的命令或脚本: strings /path/to/the/file 3. 扫描系统…...

【学习计算机视觉算法的基础及基本编码-基于Python语言--实例教程】
Python视觉算法实际从0-1实例编码 一、学习基础二、学习计算机视觉基础知识三、深度学习在计算机视觉中的应用四、实例项目五、实践与拓展 一、学习基础 数学基础 线性代数: 学习矩阵、向量的基本概念,包括矩阵的加法、乘法、转置等运算。理解矩阵的秩、…...

从零搭建一个Vue3 + Typescript的脚手架——day1
1.开发环境搭建 (1).配置vite vite简介 Vite 是一个由尤雨溪开发的现代化前端构建工具,它利用了浏览器对 ES 模块的原生支持,极大地提升了开发服务器的启动速度和热更新效率。Vite 不仅适用于 Vue.js,还支持 React、Svelte 等多种框架&…...

Pgsql存储占用分析
基础命令 -- 查询表大小 SELECT pg_total_relation_size(table_name);-- 查询表大小(不带索引) SELECT pg_table_size(table_name);-- 查询表索引大小 SELECT pg_indexes_size(table_name);-- 查询表具体大小 SELECT pg_relation_size(table_name); SEL…...

51c自动驾驶~合集46
我自己的原文哦~ https://blog.51cto.com/whaosoft/13050104 #世界模型会是L3自动驾驶的唯一解吗 三维空间占有率(3D Occupancy)预测的目的是预测三维空间中的每个体素是否被占有,如果被占有,则对应的体素将被标记。3D Semant…...

Elasticsearch:使用全文搜索在 ES|QL 中进行过滤 - 8.17
8.17 在 ES|QL 中引入了 match 和 qstr 函数,可用于执行全文过滤。本文介绍了它们的作用、使用方法、与现有文本过滤方法的区别、当前的限制以及未来的改进。 ES|QL 现在包含全文函数,可用于使用文本查询过滤数据。我们将回顾可用的文本过滤方法…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
