uniapp区域滚动——上划进行分页加载数据(详细教程)
##标题
用来总结和学习,便于自己查找
文章目录
一、为什么scroll-view?
1.1 区域滚动页面滚动?
1.2 代码?
二、分页功能?
2.1 如何实现?
2.2 代码?
一、为什么scroll-view?
解释:因为我要实现区域滚动以及分页加载,刚开始使用css的overflow 样式但是实现分页的时候检测不到,
就先只能用scroll-view来实现、但是文档写到会影响性能,暂时数据少感觉不出来先用着,查到还有实现区
域滚动的方法虚拟滚动、<u-list> 和 u-pagination这几种方法、后续可以试一试要是能试通会写在后续文章
里面


1.1 区域滚动页面滚动
就是不是再整个页面进行滚动,而是上面有一部分东西,底下有一部分进行滚动就如底下图片所示
1.2 代码
<scroll-view style="height: 70vh;" :scroll-top="scrollTop" scroll-y="true" @scroll="onScroll"@scrolltolower="onScrollToLower" lower-threshold="50"><!-- <view class="alalmlist" bindscroll="onScroll"> --><view class="care" v-show="careShow" v-for="(item, index) in notification" :key="index"><view class="careText"></view></view><!-- </view> --></scroll-view>
scroll-view把你遍历的东西包裹起来就行style="height: 70vh;"这个要设置高度@scrolltolower=“onScrollToLower” lower-threshold="50"这个就是触底50的时候检测到就触发了onScrollToLower这个函数写分页逻辑即可
二、分页功能?
后台的分页见过哈,一样的不过是竖着的
2.1 如何实现?
思路就是用到触底函数scrolltolower就是上面我说的,触底的时候加载分页,(这个说明一下,后端给你同一个接口里面有两个参数pages,和pagesize,第一个参数pages就是一页的意思,pagesize就是每页有多少条,然后后段会给你返回一个总条数加载完停止加载用的)
2.2 代码?
async searchFoods() {try {const res = await list({action: "list",page_index: this.page,page_size: "5"});if (res.Status) {const data = res.Result;if (res.end<= this.notification.length) {return}this.notification.push(...data)}} catch (err) {console.log(err);}}
解释一下:这个就是触底触发的函数, page_index: this.page,触底之后 this.page要加一,请求下一页的数据page_size这个就是每页显示的条数,res.end这个就是总条数,要是达到总条数就不加载了
相关文章:

uniapp区域滚动——上划进行分页加载数据(详细教程)
##标题 用来总结和学习,便于自己查找 文章目录 一、为什么scroll-view? 1.1 区域滚动页面滚动? 1.2 代码? 二、分页功能? 2.1 如何实现ÿ…...

机器学习(1):线性回归概念
1 线性回归基础 1.1 什么是线性 例如:汽车每小时60KM,3小时可以行使多长距离?已知汽车的速度,则汽车的行使距离只与时间唯一相关。在二元的直角坐标系中,描出这一关系的图是一条直线,所以称为线性关系。 线…...

关于编写测试用例的细枝末节
这里写目录标题 故障判别类-边界考虑示例1.0:若A>20.3且持续时间≥15ms时(判故周期为1000Hz),输出B为1,否则输出B为0。 故障判别类-不可恢复测试示例1.1:若A>20.3且持续时间≥15ms时…...

《计算机网络》课后探研题书面报告_了解PPPoE协议
PPPoE协议的工作原理与应用分析 摘 要 PPPoE(Point-to-Point Protocol over Ethernet)是一种广泛应用于宽带接入的网络协议,特别是在DSL(数字用户线路)和光纤网络中具有重要的应用价值。PPPoE结合了PPP协议的认证、加…...

Linux Centos 安装Jenkins到服务
一、前言 假设你已经下载了jenkins.war 安装了对应的jdk,下面我们来安装jenkins,以服务的形式安装。 二、安装 1)将jenkins.war拷贝到合适的位置,我的位置 /u01/jenkins/ ,位置你自己选。 2)创建系统用户…...

解决“无法定位程序输入点 av_buffer_create 于动态链接库 XXX\Obsidian.exe 上”问题
解决“无法定位程序输入点 av_buffer_create 于动态链接库 XXX\Obsidian.exe 上”问题 问题描述 本人在使用zotero中的zotero one(青柠学术插件)的时候,使用插件跳转obsidian中的对应笔记,出现上图情况。(错误中提到的…...

基于考研概率论知识解读 Transformer:为何自注意力机制要除以根号 dk
Transformer自注意力机制中除以 d k \sqrt{d_k} dk 深度剖析 【 Transformer 系列,故事从 d k \sqrt{d_k} dk 说起】 LLM这么火,Transformer厥功甚伟,某天心血来潮~,再去看看! 它长这个样子: 深入…...

网络安全学习81天(记录)
前言: 小迪安全,81天,开始了php代码审计 思路: 内容: #知识点: 1、审计漏洞-SQL 数据库注入挖掘 1、审计思路-正则搜索&功能追踪&辅助工具 3、审计类型-常规架构&MVC 架构&三方框架 #章…...
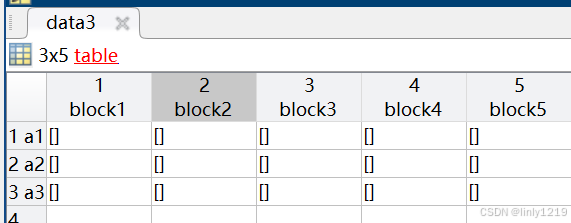
MATLAB学习笔记-table
1.在table中叠加table table 的每一列具有固定的数据类型。如果要让表的所有单元格都可以任意填充,就得让每一列都是 cell 类型,这样表中每个单元格都是“一个元胞”。创建时可以先构造一个 空 cell 数组(大小为行数列数)&#x…...

mybatisPlus(条件构造器API)
文章目录 目录一、mybatisPlus的介绍二、mybatisPlus的基础使用配置BaseMapper的基本CURD(增删改查) 三、wrapper(条件构造器)条件构造器(wrapper)通用API基础条件判断:进阶条件判断(…...

5G+工业互联网迈入规模化发展新阶段
百度安全验证 https://blog.csdn.net/qq_25467441/article/details/145036191?sharetypeblogdetail&sharerId145036191&sharereferPC&sharesourceqq_25467441&spm1011.2480.3001.8118 好看视频-轻松有收获 产业供给加速提升。国内主流模组厂商引领全球5G模组…...

【CI/CD构建】关于不小心将springMVC注解写在service层
背景 之前写一个接口的时候没有察觉到将RequestBody这个注解带到service层了。 今天提交代码的时候,插件没有检测到这个低级错误,导致试飞构建连maven编译都过不了,maven找不到程序包org.springframework.web.bind.annotation这个包 结果…...

《鸿蒙Next ArkTS:开启人工智能应用开发高效新旅程》
在当今科技飞速发展的时代,人工智能与鸿蒙Next的结合正成为开发者们关注的焦点。利用鸿蒙Next的ArkTS语言开发高效的人工智能驱动的应用程序,为我们带来了前所未有的机遇和创新空间。 了解ArkTS语言与鸿蒙Next ArkTS是一种基于TypeScript的静态类型脚本…...

Unity 3D游戏开发从入门进阶到高级
本文精心整理了Unity3D游戏开发相关的学习资料,涵盖入门、进阶、性能优化、面试和书籍等多个维度,旨在为Unity开发者提供全方位、高含金量的学习指南.欢迎收藏。 学习社区 Unity3D开发者 这是一个专注于Unity引擎的开发者社区,汇聚了众多Un…...

什么是SSH登录?SSH客户端软件有哪些?
一、SSH解释 SSH(Secure Shell)登录是一种用于计算机之间加密登录的网络协议。SSH登录允许用户通过互联网访问、控制和修改远程服务器。它提供了加密的通信通道,以保护敏感数据的机密性和完整性。SSH协议支持多种应用,包括SSH&…...

Ubuntu服务器提示:检测到存在恶意文件,补救思路
1. 确定文件类型 可以使用file命令来检查该文件的类型,这有助于判断它是否真的是一个恶意文件 file /path/to/the/file 2. 检查文件内容 使用strings命令查看文件内容,看是否有可疑的命令或脚本: strings /path/to/the/file 3. 扫描系统…...

【学习计算机视觉算法的基础及基本编码-基于Python语言--实例教程】
Python视觉算法实际从0-1实例编码 一、学习基础二、学习计算机视觉基础知识三、深度学习在计算机视觉中的应用四、实例项目五、实践与拓展 一、学习基础 数学基础 线性代数: 学习矩阵、向量的基本概念,包括矩阵的加法、乘法、转置等运算。理解矩阵的秩、…...

从零搭建一个Vue3 + Typescript的脚手架——day1
1.开发环境搭建 (1).配置vite vite简介 Vite 是一个由尤雨溪开发的现代化前端构建工具,它利用了浏览器对 ES 模块的原生支持,极大地提升了开发服务器的启动速度和热更新效率。Vite 不仅适用于 Vue.js,还支持 React、Svelte 等多种框架&…...

Pgsql存储占用分析
基础命令 -- 查询表大小 SELECT pg_total_relation_size(table_name);-- 查询表大小(不带索引) SELECT pg_table_size(table_name);-- 查询表索引大小 SELECT pg_indexes_size(table_name);-- 查询表具体大小 SELECT pg_relation_size(table_name); SEL…...

51c自动驾驶~合集46
我自己的原文哦~ https://blog.51cto.com/whaosoft/13050104 #世界模型会是L3自动驾驶的唯一解吗 三维空间占有率(3D Occupancy)预测的目的是预测三维空间中的每个体素是否被占有,如果被占有,则对应的体素将被标记。3D Semant…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
