【线性代数】行列式的概念
d e t ( A ) = ∑ i 1 , i 2 , ⋯ , i n ( − 1 ) σ ( i 1 , ⋯ , i n ) a 1 , i 1 a 2 , i 2 , ⋯ , a n , i n det(A) =\sum_{i_1,i_2,\cdots,i_n } (-1)^{\sigma(i_1,\cdots,i_n)} a_{1,i_1}a_{2,i_2},\cdots, a_{n,i_n} det(A)=i1,i2,⋯,in∑(−1)σ(i1,⋯,in)a1,i1a2,i2,⋯,an,in
i 1 , ⋯ , i n i_1,\cdots,i_n i1,⋯,in 是 1 , ⋯ , n 1,\cdots,n 1,⋯,n 的排列.
计算复杂度
O ( n ⋅ n ! ) O(n\cdot n!) O(n⋅n!)
{ 1 , 2 } \{1,2\} {1,2} 的全排列如下
| 排列 | 逆序数 | 奇偶性 |
|---|---|---|
| 1 , 2 1,2 1,2 | 0 | 偶 |
| 2 , 1 2,1 2,1 | 1 | 奇 |
[ a 1 , 1 a 1 , 2 a 2 , 1 a 2 , 2 ] \left[\begin{matrix}a_{1,1} &a_{1,2}\\ a_{2,1} & a_{2,2}\end{matrix}\right] [a1,1a2,1a1,2a2,2]
{ 1 , 2 , 3 } \{1,2,3\} {1,2,3} 的全排列如下
| 排列 | 逆序数 | 奇偶性 |
|---|---|---|
| 1 , 2 , 3 1,2,3 1,2,3 | 0 | 偶 |
| 1 , 3 , 2 1,3,2 1,3,2 | 1 | 奇 |
| 2 , 1 , 3 2,1,3 2,1,3 | 1 | 奇 |
| 2 , 3 , 1 2,3,1 2,3,1 | 2 | 偶 |
| 3 , 1 , 2 3,1,2 3,1,2 | 2 | 偶 |
| 3 , 2 , 1 3,2,1 3,2,1 | 3 | 奇 |
[ a 1 , 1 a 1 , 2 a 1 , 3 a 2 , 1 a 2 , 2 a 2 , 3 a 3 , 1 a 3 , 2 a 3 , 3 ] \left[\begin{matrix}a_{1,1} &a_{1,2} & a_{1,3}\\ a_{2,1} & a_{2,2}& a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3}\end{matrix}\right] a1,1a2,1a3,1a1,2a2,2a3,2a1,3a2,3a3,3
递归法生成全排列
using CSV, DataFrames, Tables
function OE(sigma) # 判断奇偶置换n=length(sigma); out=1for i=1:nfor j=1:n-1if sigma[j] > sigma[j+1]out=-out; sigma[j],sigma[j+1]=sigma[j+1], sigma[j]endendendreturn(out)
end
function remove_last(seq) # 删除序列最后一个元素
lth=length(seq)
z=copy(seq[1:lth-1])
return(z)
end
function rankfull(seq,n,cpl) # 递归全排列生成器lth=length(seq)if lth==1m=[cpl; seq]open("rankfull_sol.txt","a") do iofor i=1:ns=m[i]; write(io, "$s,")endwrite(io,"\n");endelsefor i=1:lths=seq[i]; idx=0;list=zeros(Int,lth-1)for j=1:lthif !(seq[j]==s)idx=idx+1; list[idx]=seq[j]endendcpl=[cpl; s];rankfull(list,n,cpl)cpl=remove_last(cpl)endend
end
function det_defn(A) # 定义法求行列式lth=size(A,1)seq=1:lthglobal ranksol=[seq];lth=length(seq); cpl=[]; iters=factorial(lth)tryrankfull(seq,lth,cpl)catch nothingendio=open("rankfull_sol.txt","r")data=read(io,String)file = CSV.File(IOBuffer(data), header=false)CSV.write("fullrank.csv", file)close(io)sigma=zeros(Int64,iters,lth);for i=1:factorial(lth)for j=1:lthsigma[i,j]=file[i][j]endendDETs=0*A[1,1]for i=1:itersPrs=1for j=1:lthPrs=Prs*M[j,sigma[i,j]]endDETs=DETs+ OE(sigma[i,:])*Prsendreturn(DETs)
end
M=[4//1 3 2 1;3 2 1 4;2 1 4 3;1 4 3 2]
a= det_defn(M)
println("\n")
println("defn=",a)
-160//1
邻近对换算法生成全排列
function ranking(lth) # 邻近对换全排列生成器prd=1; arr=zeros(Int64,lth);for i=1:lth arr[i]=i endfor i=1:lth prd=prd*i endjx=lth ; dr=-1; s=0;for j=1:prdif dr<0if jx>1arr[jx],arr[jx+dr] = arr[jx+dr],arr[jx]jx=jx+drelsearr[lth],arr[lth-1] = arr[lth-1],arr[lth]dr=-drendelseif jx<ltharr[jx],arr[jx+dr] = arr[jx+dr],arr[jx];jx=jx+drelsearr[1],arr[2] = arr[2],arr[1]; dr=-drendendopen("ranking_sol.txt","a") do iofor i=1:lths=arr[i]; write(io, "$s,")endwrite(io,"\n");end end
end
function det_defn2(A) # 定义法求行列式lth=size(A,1)seq=1:lthglobal ranksol=[seq];lth=length(seq); cpl=[]; iters=factorial(lth)try rm("ranking_sol.txt")catchnothingendranking(lth)io=open("ranking_sol.txt","r")data=read(io,String)file = CSV.File(IOBuffer(data), header=false)CSV.write("fullrank.csv", file)close(io)sigma=zeros(Int64,iters,lth);for i=1:factorial(lth)for j=1:lthsigma[i,j]=file[i][j]endendDETs=0*A[1,1]for i=1:itersPrs=1for j=1:lthPrs=Prs*M[j,sigma[i,j]]endDETs=DETs+ OE(sigma[i,:])*Prsendreturn(DETs)
end
M=[4//1 3 2 ;3 2 1 ;2 1 4]
a= det_defn2(M)
-160//1
相关文章:

【线性代数】行列式的概念
d e t ( A ) ∑ i 1 , i 2 , ⋯ , i n ( − 1 ) σ ( i 1 , ⋯ , i n ) a 1 , i 1 a 2 , i 2 , ⋯ , a n , i n det(A) \sum_{i_1,i_2,\cdots,i_n } (-1)^{\sigma(i_1,\cdots,i_n)} a_{1,i_1}a_{2,i_2},\cdots, a_{n,i_n} det(A)i1,i2,⋯,in∑(−1)σ(i1,⋯,in)a1…...
)
Android SystemUI——StatusBar视图创建(六)
上一篇文章我们介绍了 StatusBar 的构建过程,在 makeStatusBarView() 中获得 FragmentHostManager,用来管理 StatusBar 的窗口。 一、状态栏视图 在得到 FragmentHostManager 实例对象之后,还会继续调用 addTagListener() 方法设置监听对象,然后获取 FragmentManager 并开…...

Picocli 命令行框架
官方文档 https://picocli.info/ 官方提供的快速入门教程 https://picocli.info/quick-guide.html 使用 Picocli 创建命令行应用程序 Picocli 是一个用于构建 Java 命令行应用的强大框架,它简化了参数解析和帮助消息生成的过程。 下面是如何使用 Picocli 构建简单命…...

spring-cloud-starter-gateway 使用中 KafkaAppender的问题
公司需要将应用日志上报到kafka,以供分析与查看。 结合logback可以完成此功能,大致配置如下: <appender name"KafkaAppender" class"com.github.danielwegener.logback.kafka.KafkaAppender"><encoder class&…...

【全套】基于分类算法的学业警示预测信息管理系统
【全套】基于分类算法的学业警示预测信息管理系统 【摘 要】 随着网络技术的发展基于分类算法的学业警示预测信息管理系统是一种新的管理方式,同时也是现代学业预测信息管理的基础,利用互联网的时代与实际情况相结合来改变过去传统的学业预测信息管理中…...

Elasticsearch Python 客户端是否与自由线程 Python 兼容?
作者:来自 Elastic Quentin_Pradet 在这篇文章中,我们将进行一些实验,看看 Python Elasticsearch 客户端是否与新的 Python 3.13 自由线程(free-threading)版本兼容,其中 GIL 已被删除。 介绍 但首先&…...

基于大语言模型的组合优化
摘要:组合优化(Combinatorial Optimization, CO)对于提高工程应用的效率和性能至关重要。随着问题规模的增大和依赖关系的复杂化,找到最优解变得极具挑战性。在处理现实世界的工程问题时,基于纯数学推理的算法存在局限…...

#CSS混合模式:解决渐变背景下的文字可见性问题
在现代网页设计中,渐变背景的使用越来越普遍。然而,当我们在渐变背景上放置文字时,常常会遇到一个问题:文字在某些背景颜色下可能变得难以阅读。今天,我们将探讨一个优雅的解决方案:使用CSS混合模式。 问题…...

Vue2+OpenLayers给标点Feature添加信息窗体(提供Gitee源码)
目录 一、案例截图 二、安装OpenLayers库 三、代码实现 3.1、信息窗体DOM元素 3.2、创建Overlay 3.3、创建一个点 3.4、给点初始化点击事件 3.5、完整代码 四、Gitee源码 一、案例截图 二、安装OpenLayers库 npm install ol 三、代码实现 初始化变量: d…...

实战threeJS数字孪生开源 数字工厂
threeJS数字孪生 数字工厂 设备定位 基于three.js的数字工厂开源项目介绍 一、项目概述 本项目是一款基于three.js的数字工厂项目,旨在通过3D可视化技术,为工业制造领域提供一个直观、高效、智能的生产监控与管理平台。该项目结合了现代前端技术栈&…...

【Python基础篇】——第3篇:从入门到精通:掌握Python数据类型与数据结构
第3篇:数据类型与数据结构 目录 Python中的数据类型概述列表(List) 创建列表列表的基本操作列表方法列表推导式 元组(Tuple) 创建元组元组的基本操作元组的不可变性 字典(Dictionary) 创建字典…...

算法3(力扣83)-删除链表中的重复元素
1、题目:给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。 2、实现( 因为已排序,所以元素若重复,必然在其下一位)(这里为在vscod…...

HarmonyOS 鸿蒙 ArkTs(5.0.1 13)实现Scroll下拉到顶刷新/上拉触底加载,Scroll滚动到顶部
HarmonyOS 鸿蒙 ArkTs(5.0.1 13)实现Scroll下拉到顶刷新/上拉触底加载 效果展示 使用方法 import LoadingText from "../components/LoadingText" import PageToRefresh from "../components/PageToRefresh" import FooterBar from "../components/…...

.NET8.0多线程编码结合异步编码示例
1、创建一个.NET8.0控制台项目来演示多线程的应用 2、快速创建一个线程 3、多次运行程序,可以得到输出结果 这就是多线程的特点 - 当多个线程并行执行时,它们的具体执行顺序是不确定的,除非我们使用同步机制(如 lock、信号量等&am…...

SpringBoot项目中解决CORS跨域资源共享问题
在Spring Boot项目中解决CORS(跨域资源共享)问题,可以通过以下几种方法: 1. 使用CrossOrigin注解 这是最简单的方法,适用于单个控制器或控制器方法级别的跨域配置。你可以在控制器类或具体的方法上使用CrossOrigin注…...

Android string.xml中特殊字符转义
项目中要在string.xml 中显示特殊符号 空格: (普通的英文半角空格但不换行) 窄空格: (中文全角空格 (一个中文宽度)) (半个中文宽度,但两个空格比一个中文…...

解析传统Workflow、AI Workflow与AI Agent概念,并通过Coze案例探讨利用AI工作流构建应用的实践流程
传统工作流 工作流入门这篇就够了 BPMN.JS中文教程 BPMN 工作流引擎解析 定义:工作流是在计算机支持下业务流程的自动或半自动化,其通过对流程进行描述以及按一定规则执行以完成相应工作。 应用:随着计算机技术的发展以及工业生产、办公自动…...

光谱相机的光谱分辨率可以达到多少?
多光谱相机 多光谱相机的光谱分辨率相对较低,波段数一般在 10 到 20 个左右,光谱分辨率通常在几十纳米到几百纳米之间,如常见的多光谱相机光谱分辨率为 100nm 左右。 高光谱相机 一般的高光谱相机光谱分辨率可达 2.5nm 到 10nm 左右&#x…...

android Recyclerview viewholder统一封装
Recyclerview holder 统一封装 ViewHolder类 import android.annotation.SuppressLint import android.content.Context import android.graphics.Color import android.graphics.drawable.GradientDrawable import android.os.Build import android.os.CountDownTimer import…...
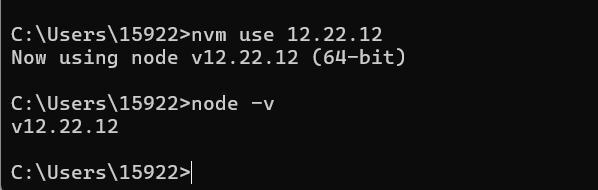
Windows部署NVM并下载多版本Node.js的方法(含删除原有Node的方法)
本文介绍在Windows电脑中,下载、部署NVM(node.js version management)环境,并基于其安装不同版本的Node.js的方法。 在之前的文章Windows系统下载、部署Node.js与npm环境的方法(https://blog.csdn.net/zhebushibiaoshi…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
