深度解析统计学四大分布:Z、卡方、t 与 F 的关联与应用
统计学关键分布:Z、卡方、t、F 的关系探秘与应用指南
A/B实验系列相关文章(置顶)
1. A/B实验之置信检验(一):如何避免误判和漏报
2. A/B实验之置信检验(二):置信检验精要
3. A/B实验之置信检验(三):序贯检验
4. 卡方分布:理论、应用与实例解析
5. 深入理解P值与置信度检验:概念、方法及实例解析
6. 深度解析统计学四大分布:Z、卡方、t 与 F 的关联与应用
7. 中心极限定理:以番茄为引串联 Z、卡方、t 、F 分布
一、引言
在统计学领域,Z分布、卡方分布、t分布与F分布是极为重要的概率分布,它们在数据的分析与推断中发挥着关键作用。无论是科学研究、质量控制,还是工业界 AB Test 等场景,这些分布都为理解和解读数据提供了有力工具。本文将深入探讨t分布与F分布的产生背景、构造思路、特点及适用场景,并与Z分布、卡方分布进行对比,辅以具体例子,助力读者全面掌握这些重要概念。
二、四种分布的对比
为更清晰地理解这四种分布,以下从常见数学角度进行对比:
| 分布名称 | 定义与公式 | 分布形状 | 参数特点 | 均值与方差 | 常见应用场景 | 与其他分布关系 |
|---|---|---|---|---|---|---|
| Z分布(标准正态分布) | 若随机变量 Z Z Z的概率密度函数为 f ( z ) = 1 2 π e − z 2 2 f(z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{z^{2}}{2}} f(z)=2π1e−2z2, − ∞ < z < + ∞ -\infty < z < +\infty −∞<z<+∞,则 Z Z Z服从标准正态分布,记作 Z ∼ N ( 0 , 1 ) Z \sim N(0, 1) Z∼N(0,1) | 钟形对称,关于 z = 0 z = 0 z=0对称 | 无额外参数,固定为均值 μ = 0 \mu = 0 μ=0,标准差 σ = 1 \sigma = 1 σ=1 | 均值 E ( Z ) = 0 E(Z)=0 E(Z)=0,方差 D ( Z ) = 1 D(Z)=1 D(Z)=1 | 1. 总体标准差已知时,对总体均值的假设检验,如 Z = X ˉ − μ σ n Z=\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}} Z=nσXˉ−μ用于单样本均值检验 2. 大样本情况下,对比例的假设检验 | 是正态分布的标准化形式,许多其他分布在一定条件下可近似为正态分布进而与Z分布关联 |
| 卡方分布 | 设 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn是相互独立且都服从标准正态分布 N ( 0 , 1 ) N(0, 1) N(0,1)的随机变量,则 Y = ∑ i = 1 n X i 2 Y = \sum_{i=1}^{n}X_{i}^{2} Y=∑i=1nXi2服从自由度为 n n n的卡方分布,记作 Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n) | 当自由度 n n n较小时,分布呈右偏态;随着 n n n增大,逐渐趋近于正态分布 | 自由度 n n n, n n n决定分布形状 | 均值 E ( χ 2 ( n ) ) = n E(\chi^{2}(n)) = n E(χ2(n))=n,方差 D ( χ 2 ( n ) ) = 2 n D(\chi^{2}(n)) = 2n D(χ2(n))=2n | 1. 总体方差的区间估计与假设检验 2. 拟合优度检验,判断样本数据是否符合某种理论分布 3. 独立性检验,判断两个分类变量是否相互独立 | 1. 若 Z ∼ N ( 0 , 1 ) Z \sim N(0, 1) Z∼N(0,1),则 Z 2 ∼ χ 2 ( 1 ) Z^{2} \sim \chi^{2}(1) Z2∼χ2(1) 2. 是 t t t分布和 F F F分布构造的基础之一 |
| t分布 | 设随机变量 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1), Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n),且 X X X与 Y Y Y相互独立,则 T = X Y n T = \frac{X}{\sqrt{\frac{Y}{n}}} T=nYX服从自由度为 n n n的 t t t分布,记作 T ∼ t ( n ) T \sim t(n) T∼t(n) | 与标准正态分布类似,关于 t = 0 t = 0 t=0对称,但在小样本时尾部比标准正态分布更厚,极端值出现概率更大 | 自由度 n n n, n n n影响分布形状 | 当 n > 1 n > 1 n>1时,均值 E ( t ( n ) ) = 0 E(t(n)) = 0 E(t(n))=0;当 n > 2 n > 2 n>2时,方差 D ( t ( n ) ) = n n − 2 D(t(n))=\frac{n}{n - 2} D(t(n))=n−2n | 1. 总体标准差未知时,对总体均值的假设检验,如单样本 t t t检验、独立样本 t t t检验、配对样本 t t t检验 2. 小样本情况下的区间估计 | 1. 当自由度 n n n较大( n ≥ 30 n \geq 30 n≥30)时, t t t分布近似于标准正态分布 2. 若 T ∼ t ( n ) T \sim t(n) T∼t(n),则 T 2 ∼ F ( 1 , n ) T^{2} \sim F(1, n) T2∼F(1,n) |
| F分布 | 设随机变量 U ∼ χ 2 ( n 1 ) U \sim \chi^{2}(n_1) U∼χ2(n1), V ∼ χ 2 ( n 2 ) V \sim \chi^{2}(n_2) V∼χ2(n2),且 U U U与 V V V相互独立,则 F = U n 1 V n 2 F=\frac{\frac{U}{n_1}}{\frac{V}{n_2}} F=n2Vn1U服从自由度为 ( n 1 , n 2 ) (n_1, n_2) (n1,n2)的 F F F分布,记作 F ∼ F ( n 1 , n 2 ) F \sim F(n_1, n_2) F∼F(n1,n2),其中 n 1 n_1 n1为分子自由度, n 2 n_2 n2为分母自由度 | 形状取决于自由度 ( n 1 , n 2 ) (n_1, n_2) (n1,n2),通常为右偏态,随着 n 1 n_1 n1和 n 2 n_2 n2增大,逐渐趋近于正态分布 | 两个自由度 n 1 n_1 n1和 n 2 n_2 n2,共同决定分布形状 | 均值 E ( F ( n 1 , n 2 ) ) = n 2 n 2 − 2 E(F(n_1,n_2))=\frac{n_2}{n_2 - 2} E(F(n1,n2))=n2−2n2( n 2 > 2 n_2 > 2 n2>2),方差 D ( F ( n 1 , n 2 ) ) = 2 n 2 2 ( n 1 + n 2 − 2 ) n 1 ( n 2 − 2 ) 2 ( n 2 − 4 ) D(F(n_1,n_2))=\frac{2n_2^{2}(n_1 + n_2 - 2)}{n_1(n_2 - 2)^2(n_2 - 4)} D(F(n1,n2))=n1(n2−2)2(n2−4)2n22(n1+n2−2)( n 2 > 4 n_2 > 4 n2>4) | 1. 方差齐性检验,判断两个总体方差是否相等 2. 单因素方差分析,检验多个总体均值是否相等 3. 回归方程的显著性检验 | 若 F ∼ F ( n 1 , n 2 ) F \sim F(n_1, n_2) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \frac{1}{F} \sim F(n_2, n_1) F1∼F(n2,n1) |
三、四种分布的关系
- Z分布与其他分布的关系
- 与卡方分布:
若随机变量 Z Z Z 服从标准正态分布,即 Z ∼ N ( 0 , 1 ) Z \sim N(0, 1) Z∼N(0,1),则 Z 2 Z^2 Z2 服从自由度为 1 1 1 的卡方分布,可表示为:
Z 2 ∼ χ 2 ( 1 ) Z^2 \sim \chi^{2}(1) Z2∼χ2(1)
这是因为卡方分布定义为相互独立且服从标准正态分布 N ( 0 , 1 ) N(0, 1) N(0,1) 的随机变量的平方和。在此情形下,仅有一个标准正态分布随机变量 Z Z Z,其平方 Z 2 Z^2 Z2 便构成了自由度为 1 1 1 的卡方分布。 - 与t分布:
t分布基于标准正态分布(Z分布)与卡方分布构造。当总体标准差 σ \sigma σ 已知时,对于样本均值 X ˉ \bar{X} Xˉ,其标准化后的统计量服从Z分布,常用于总体均值的假设检验,如单样本情形下的检验统计量为:
Z = X ˉ − μ σ n Z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} Z=nσXˉ−μ
然而,当总体标准差 σ \sigma σ 未知,需通过样本标准差 s s s 进行估计时,构造的检验统计量服从t分布。设 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1), Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n),且 X X X 与 Y Y Y 相互独立,则 T = X Y n T = \frac{X}{\sqrt{\frac{Y}{n}}} T=nYX 服从自由度为 n n n 的t分布,记作 T ∼ t ( n ) T \sim t(n) T∼t(n)。
在大样本情况下(通常 n ≥ 30 n \geq 30 n≥30),t分布逐渐趋近于标准正态分布。这是由于随着样本量 n n n 的增大,样本标准差 s s s 对总体标准差 σ \sigma σ 的估计愈发精确,使得t分布的不确定性逐渐减小,从而趋近于Z分布。 - 与F分布:
通过t分布与F分布的关系,可间接建立Z分布与F分布的联系。已知若 T ∼ t ( n ) T \sim t(n) T∼t(n),则有:
T 2 ∼ F ( 1 , n ) T^{2} \sim F(1, n) T2∼F(1,n)
在大样本时, T T T 近似服从Z分布,由此在一定条件下,借助t分布实现了Z分布与F分布的关联。此外,在涉及F分布的方差分析等检验中,若满足正态分布假设,Z分布的性质会在推导过程中间接体现。例如,在方差分析的理论推导中,样本均值的抽样分布在一定程度上与正态分布相关,进而与Z分布产生联系,而这种联系又通过F分布的构造与性质在分析过程中得以体现。
- 与卡方分布:
- 卡方分布与其他分布的关系
- 与t分布:
t分布由一个服从标准正态分布的随机变量 X X X 和一个服从卡方分布的随机变量 Y Y Y 构造而成。设 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1), Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n),且 X X X 与 Y Y Y 相互独立,则:
T = X Y n T = \frac{X}{\sqrt{\frac{Y}{n}}} T=nYX
T T T 服从自由度为 n n n 的t分布。在此构造中,卡方分布的自由度 n n n 直接决定了t分布的自由度。卡方分布随机变量 Y Y Y 反映了样本方差的相关信息,与标准正态分布随机变量 X X X 相结合,使得t分布适用于总体标准差未知时的统计推断。例如,在单样本t检验中,通过样本数据计算出的 T T T 值,依据t分布进行总体均值的假设检验,而其中样本方差的信息通过 Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n) 得以体现。 - 与F分布:
F分布由两个独立的卡方分布随机变量构造。设 U ∼ χ 2 ( n 1 ) U \sim \chi^{2}(n_1) U∼χ2(n1), V ∼ χ 2 ( n 2 ) V \sim \chi^{2}(n_2) V∼χ2(n2),且 U U U 与 V V V 相互独立,则:
F = U n 1 V n 2 F = \frac{\frac{U}{n_1}}{\frac{V}{n_2}} F=n2Vn1U
F F F 服从自由度为 ( n 1 , n 2 ) (n_1, n_2) (n1,n2) 的F分布。卡方分布的自由度 n 1 n_1 n1 和 n 2 n_2 n2 分别作为分子自由度和分母自由度,直接决定了F分布的自由度,进而影响F分布的形状与性质。在方差分析中,通过对不同组样本方差基于卡方分布性质的分析,构建F统计量进行多个总体均值是否相等的检验。例如,组间方差和组内方差分别与卡方分布相关,通过两者的比值构造出F统计量,依据F分布判断不同总体均值是否存在显著差异。
- 与t分布:
- t分布与F分布的关系:
若 T ∼ t ( n ) T \sim t(n) T∼t(n),则:
T 2 ∼ F ( 1 , n ) T^{2} \sim F(1, n) T2∼F(1,n)
这一关系在统计检验转换及理论推导中具有重要意义。例如,在某些假设检验中,原本基于t分布的检验可通过此关系转化为基于F分布的检验,为数据分析提供了更多的方法选择与灵活性。在回归分析中,对回归系数的显著性检验有时会利用该关系,将基于t分布的检验与基于F分布的检验相联系,从不同角度验证模型的有效性。例如,在一元线性回归中,对回归系数的t检验与对回归方程整体显著性的F检验之间存在内在联系,通过 T 2 ∼ F ( 1 , n ) T^{2} \sim F(1, n) T2∼F(1,n) 的关系,可在不同检验方法之间进行转换和验证。
四、t分布
(一)定义
设随机变量 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1),即 X X X 服从标准正态分布。
设随机变量 Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n),即 Y Y Y 服从自由度为 n n n 的卡方分布。
且 X X X 与 Y Y Y 相互独立。
则随机变量 T T T 定义为:
T = X Y n T = \frac{X}{\sqrt{\frac{Y}{n}}} T=nYX
T T T 服从自由度为 n n n 的 t t t 分布,记作 T ∼ t ( n ) T \sim t(n) T∼t(n)。
(二)“t”的由来
t分布由威廉·戈塞特(William Sealy Gosset)发现并提出。当时,戈塞特在爱尔兰都柏林的吉尼斯啤酒厂工作,受公司规定限制,他只能以笔名“Student”发表研究成果。在其早期关于小样本统计的研究中,使用字母“t”来表示基于小样本的新统计量。后续为纪念他的贡献,该分布被命名为t分布,“t”也就成为此分布的特定标识。
(三)产生背景
在统计学发展早期,常假定总体服从正态分布且总体标准差已知,基于此发展出如Z检验等统计方法。然而在现实中,总体标准差往往未知。例如,研究某工厂生产的零件长度,虽可假设其服从正态分布,但因生产过程中原材料细微差异、机器磨损等因素,确切的总体标准差难以获取。在这种情况下,传统基于已知总体标准差的方法不再适用,t分布便应运而生。
(四)构造思路
t分布基于标准正态分布和卡方分布构造。
已知 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1),它可衡量数据与均值的偏离程度。
同时,引入 Y ∼ χ 2 ( n ) Y \sim \chi^{2}(n) Y∼χ2(n),卡方分布与样本方差紧密相关,能反映样本数据的离散程度。例如,从一批产品中抽取 n n n 个样本,通过计算样本与样本均值差的平方和等运算,可得到符合卡方分布的量。
让 X X X 和 Y Y Y 相互独立,构造 T T T 如下:
T = X Y n T = \frac{X}{\sqrt{\frac{Y}{n}}} T=nYX
分子 X X X 衡量样本均值与总体均值的标准化差异,分母 Y n \sqrt{\frac{Y}{n}} nY 是对样本标准差估计的一种标准化度量。通过这种构造,将样本均值与总体均值的差异,与样本标准差的估计联系起来,以适应总体标准差未知的情况。
(五)特点
- 对称性:t分布的概率密度函数关于 t = 0 t = 0 t=0 对称,与标准正态分布类似,即t分布在 t t t 轴两侧形状相同。
- 与正态分布的关系:当自由度 n n n 逐渐增大时,t分布逐渐趋近于标准正态分布 N ( 0 , 1 ) N(0, 1) N(0,1)。一般而言,当 n ≥ 30 n \geq 30 n≥30 时,t分布与标准正态分布已非常接近,实际应用中可近似使用标准正态分布。但在小样本情况( n < 30 n < 30 n<30)下,t分布的尾部比标准正态分布更厚,极端值出现的概率相对较大。
- 均值与方差:对于 T ∼ t ( n ) T \sim t(n) T∼t(n),当 n > 1 n > 1 n>1 时:
E ( T ) = 0 E(T) = 0 E(T)=0
当 n > 2 n > 2 n>2 时:
D ( T ) = n n − 2 D(T)=\frac{n}{n - 2} D(T)=n−2n
(六)适用场景与示例
- 单样本t检验:用于检验单个样本的均值是否等于某个已知值。
例如,已知某种植物在常规环境下平均高度为 μ 0 \mu_0 μ0,现改变种植环境,抽取 n n n 株植物测量高度。假设抽取 n = 20 n = 20 n=20 株,测量后计算样本均值 x ˉ \bar{x} xˉ,样本标准差 s s s。
原假设 H 0 : μ = μ 0 H_0: \mu = \mu_0 H0:μ=μ0,备择假设 H 1 : μ ≠ μ 0 H_1: \mu \neq \mu_0 H1:μ=μ0。
计算t统计量:
t = x ˉ − μ 0 s n t = \frac{\bar{x} - \mu_0}{\frac{s}{\sqrt{n}}} t=nsxˉ−μ0
若计算出的t值对应的P值小于预先设定的显著性水平(如 α = 0.05 \alpha = 0.05 α=0.05),则拒绝原假设,认为新环境下植物平均高度与 μ 0 \mu_0 μ0 有显著差异。 - 独立样本t检验:用于比较两个独立样本的均值是否来自同一总体。
例如,在药物临床试验中,将患者随机分为两组,一组服用新药,一组服用安慰剂。假设新药组有 n 1 = 30 n_1 = 30 n1=30 人,安慰剂组有 n 2 = 35 n_2 = 35 n2=35 人,治疗后测量某项指标。
原假设 H 0 : μ 1 = μ 2 H_0: \mu_1 = \mu_2 H0:μ1=μ2( μ 1 \mu_1 μ1 为新药组指标均值, μ 2 \mu_2 μ2 为安慰剂组指标均值),备择假设 H 1 : μ 1 ≠ μ 2 H_1: \mu_1 \neq \mu_2 H1:μ1=μ2。
计算t统计量:
t = x ˉ 1 − x ˉ 2 s 1 2 n 1 + s 2 2 n 2 t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} t=n1s12+n2s22xˉ1−xˉ2
其中, x ˉ 1 \bar{x}_1 xˉ1, x ˉ 2 \bar{x}_2 xˉ2 为两组样本均值, s 1 2 s_1^2 s12, s 2 2 s_2^2 s22 为两组样本方差。根据t分布判断新药是否对治疗疾病有显著效果。 - 配对样本t检验:用于检验配对数据的均值差异。
例如,对同一批学生在培训前后进行成绩测试,假设抽取 n = 50 n = 50 n=50 名学生。
原假设 H 0 : μ d = 0 H_0: \mu_d = 0 H0:μd=0( μ d \mu_d μd 为培训前后成绩差值的均值),备择假设 H 1 : μ d ≠ 0 H_1: \mu_d \neq 0 H1:μd=0。
计算t统计量:
t = d ˉ s d n t = \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}} t=nsddˉ
其中, d ˉ \bar{d} dˉ 为成绩差值的样本均值, s d s_d sd 为成绩差值的样本标准差。通过t分布判断培训是否有效。
五、F分布
(一)定义
设随机变量 U ∼ χ 2 ( n 1 ) U \sim \chi^{2}(n_1) U∼χ2(n1),即 U U U 服从自由度为 n 1 n_1 n1 的卡方分布。
设随机变量 V ∼ χ 2 ( n 2 ) V \sim \chi^{2}(n_2) V∼χ2(n2),即 V V V 服从自由度为 n 2 n_2 n2 的卡方分布。
且 U U U 与 V V V 相互独立。
则随机变量 F F F 定义为:
F = U n 1 V n 2 F=\frac{\frac{U}{n_1}}{\frac{V}{n_2}} F=n2Vn1U
F F F 服从自由度为 ( n 1 , n 2 ) (n_1, n_2) (n1,n2) 的 F F F 分布,记作 F ∼ F ( n 1 , n 2 ) F \sim F(n_1, n_2) F∼F(n1,n2),其中 n 1 n_1 n1 称为分子自由度, n 2 n_2 n2 称为分母自由度。
(二)“F”的由来
F分布由著名统计学家罗纳德·艾尔默·费希尔(Ronald Aylmer Fisher)提出。为纪念费希尔在方差分析等统计学领域的卓越贡献,乔治·W·斯内德克(George W. Snedecor)将这种用于方差分析和比较的分布命名为F分布,“F”取自费希尔(Fisher)的首字母。费希尔在统计学发展中地位举足轻重,提出了诸多重要统计方法与理论,F分布便是其中之一,在方差分析、回归分析等方面应用广泛。
(三)产生背景
在实际研究中,常需比较多个总体的方差或均值,如比较不同肥料对农作物产量的影响,或不同教学方法对学生成绩的影响等。为有效解决这类问题,F分布被引入统计学。它主要用于分析不同组数据的离散程度,帮助判断不同组数据之间的差异是由随机因素造成,还是确实存在显著差异。
(四)构造思路
F分布基于两个独立的卡方分布构造。
已知两个独立随机变量 U ∼ χ 2 ( n 1 ) U \sim \chi^{2}(n_1) U∼χ2(n1) 和 V ∼ χ 2 ( n 2 ) V \sim \chi^{2}(n_2) V∼χ2(n2),其中 n 1 n_1 n1 和 n 2 n_2 n2 分别是它们的自由度。
构造 F F F 如下:
F = U n 1 V n 2 F=\frac{\frac{U}{n_1}}{\frac{V}{n_2}} F=n2Vn1U
分子 U n 1 \frac{U}{n_1} n1U 是对自由度为 n 1 n_1 n1 的卡方分布变量 U U U 的平均化处理,反映一种平均离散程度;分母 V n 2 \frac{V}{n_2} n2V 是对自由度为 n 2 n_2 n2 的卡方分布变量 V V V 的平均化处理,反映另一种平均离散程度。通过两者的比值,可比较这两种离散程度之间的关系。
(五)特点
- 非负性:F分布的取值范围是 ( 0 , + ∞ ) (0, +\infty) (0,+∞),因为它由两个卡方分布随机变量的比值构成,而卡方分布本身是非负的。
- 形状依赖自由度:F分布的形状取决于分子自由度 n 1 n_1 n1 和分母自由度 n 2 n_2 n2。不同的自由度组合会导致F分布的形状差异较大。一般来说,当 n 1 n_1 n1 和 n 2 n_2 n2 都较小时,F分布呈右偏态;随着 n 1 n_1 n1 和 n 2 n_2 n2 的增大,F分布逐渐趋近于正态分布。
- 倒数性质:若 F ∼ F ( n 1 , n 2 ) F \sim F(n_1, n_2) F∼F(n1,n2),则:
1 F ∼ F ( n 2 , n 1 ) \frac{1}{F} \sim F(n_2, n_1) F1∼F(n2,n1)
这一性质在一些统计计算和检验中非常有用,例如在双侧F检验中,可利用此性质简化计算。
(六)适用场景与示例
- 方差齐性检验:用于判断两个总体的方差是否相等。
例如,在比较两个班级学生的考试成绩稳定性时,假设班级A有 n 1 = 40 n_1 = 40 n1=40 名学生,班级B有 n 2 = 45 n_2 = 45 n2=45 名学生。
计算两个班级成绩的样本方差 s 1 2 s_1^2 s12 和 s 2 2 s_2^2 s22,构造F统计量:
F = s 1 2 s 2 2 F = \frac{s_1^2}{s_2^2} F=s22s12(假设 s 1 2 ≥ s 2 2 s_1^2 \geq s_2^2 s12≥s22)
原假设 H 0 : σ 1 2 = σ 2 2 H_0: \sigma_1^2 = \sigma_2^2 H0:σ12=σ22( σ 1 2 \sigma_1^2 σ12, σ 2 2 \sigma_2^2 σ22 为两个班级成绩的总体方差),备择假设 H 1 : σ 1 2 ≠ σ 2 2 H_1: \sigma_1^2 \neq \sigma_2^2 H1:σ12=σ22。根据F分布判断两个班级成绩的方差是否相同,以决定后续使用何种统计方法进行均值比较。 - 单因素方差分析:用于检验多个总体均值是否相等。
例如,研究三种不同品种的小麦在相同种植条件下的产量是否有显著差异。假设每种品种种植 n = 25 n = 25 n=25 块地,分别计算每个品种小麦产量的均值和组内方差。
原假设 H 0 : μ 1 = μ 2 = μ 3 H_0: \mu_1 = \mu_2 = \mu_3 H0:μ1=μ2=μ3( μ 1 \mu_1 μ1, μ 2 \mu_2 μ2, μ 3 \mu_3 μ3 为三种品种小麦产量的总体均值),备择假设 H 1 H_1 H1:至少有两个总体均值不相等。通过计算组间方差和组内方差构造F统计量:
F = 组间方差 组内方差 F = \frac{组间方差}{组内方差} F=组内方差组间方差
依据F分布判断这些总体均值是否来自同一个总体。 - 回归方程的显著性检验:在回归分析中,检验自变量对因变量的解释能力是否显著。
例如,建立一个关于销售额与广告投入、价格等自变量的回归方程。
原假设 H 0 H_0 H0:所有自变量的系数都为0,即自变量对因变量无显著影响。
通过计算回归平方和与残差平方和构造F统计量:
F = 回归平方和 / 自变量个数 残差平方和 / ( n − 自变量个数 − 1 ) F = \frac{回归平方和 / 自变量个数}{残差平方和 / (n - 自变量个数 - 1)} F=残差平方和/(n−自变量个数−1)回归平方和/自变量个数
其中, n n n 为样本数量。根据F分布判断回归方程整体是否显著,即所有自变量作为一个整体对因变量是否有显著影响。
六、结论
Z分布、卡方分布、t分布与F分布在统计学中各具重要作用且相互关联。t分布解决了总体标准差未知时样本推断总体的难题,尤其在小样本情况下表现出色;F分布则主要用于方差比较和多总体均值检验等场景。深入理解这些分布的定义、特点、应用场景以及它们之间的关系,对科研工作者、数据分析人员以及各领域决策者至关重要,有助于从数据中挖掘有价值的信息,做出科学合理的决策。
相关文章:

深度解析统计学四大分布:Z、卡方、t 与 F 的关联与应用
统计学关键分布:Z、卡方、t、F 的关系探秘与应用指南 A/B实验系列相关文章(置顶) 1. A/B实验之置信检验(一):如何避免误判和漏报 2. A/B实验之置信检验(二):置信检验精要…...

zkServer.sh脚本
Apache ZooKeeper 几种常见的方法: 一、使用 zkServer.sh 脚本: 最常见的启动 ZooKeeper 的方式是使用提供的 zkServer.sh 脚本。此脚本可用于管理 ZooKeeper 进程。以下是一些示例命令: 1. 在前台启动 ZooKeeper: ./zkServer.s…...

CV(10)--目标检测
前言 仅记录学习过程,有问题欢迎讨论 目标检测 object detection,就是在给定的图片中精确找到物体所在位置,并标注出物体的类别;输出的是分类类别label物体的外框(x, y, width, height)。 目标检测算法:…...
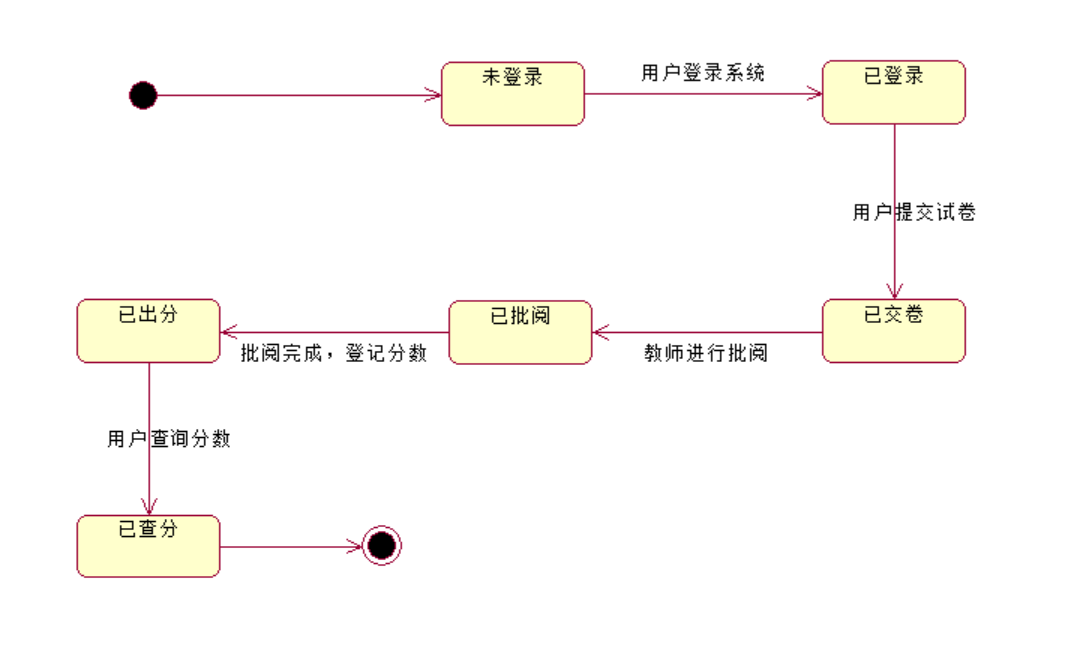
UML系列之Rational Rose笔记七:状态图
一、新建状态图 依旧是新建statechart diagram; 二、工作台介绍 接着就是一个状态的开始:开始黑点依旧可以从左边进行拖动放置: 这就是状态的开始,和活动图泳道图是一样的;只能有一个开始,但是可以有多个…...

C++单例模式的设计
单例模式(Singleton Pattern)是一种设计模式,用于确保一个类只有一个实例,并提供一个全局访问点来访问该实例。在C中,单例模式通常用于管理全局资源或共享状态。 以下是C中实现单例模式的几种常见方式: 懒…...

基于springboot的自习室预订系统
作者:学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等 文末获取“源码数据库万字文档PPT”,支持远程部署调试、运行安装。 项目包含: 完整源码数据库功能演示视频万字文档PPT 项目编码࿱…...

shell笔记
1.使用 ls -l 及 find 查找某个或者多个目录文件数量时 单个目录: find 目录 -type f|wc -l与 ls -l 目录|grep -v total|wc -l 一致 多个目录:如上结果不一致,因为 ls -l 在算多目录时,会将多目录及空格打出算作额外行 find 更精…...

《鸿蒙Next微内核:解锁人工智能决策树并行计算的加速密码》
在当今人工智能飞速发展的时代,提升运算速度是推动其进步的关键。鸿蒙Next以其独特的微内核特性,为设计决策树的并行计算框架提供了新的思路和契机。 鸿蒙Next微内核特性概述 鸿蒙Next的微内核架构将核心功能模块化,仅保留进程管理、内存管…...

AI刷题-最大矩形面积问题、小M的数组变换
目录 一、最大矩形面积问题 问题描述 输入格式 输出格式 输入样例 输出样例 数据范围 解题思路: 问题理解 数据结构选择 算法步骤 最终代码: 运行结果: 二、小M的数组变换 问题描述 测试样例 解题思路: 问题…...

Redis集群部署详解:主从复制、Sentinel哨兵模式与Cluster集群的工作原理与配置
集群部署形式 1、主从复制1.1 工作机制1.2 配置实现1.3 优缺点1.4 部署形式1.5 主从复制优化 2、Sentinel 哨兵模式2.1 工作机制2.2 配置实现2.3 优缺点2.4 哨兵机制选举流程2.5 脑裂问题解决方案 3、Redis Cluster3.1 工作机制3.2 配置实现3.3 优缺点3.4 故障转移3.5 哈希槽为…...
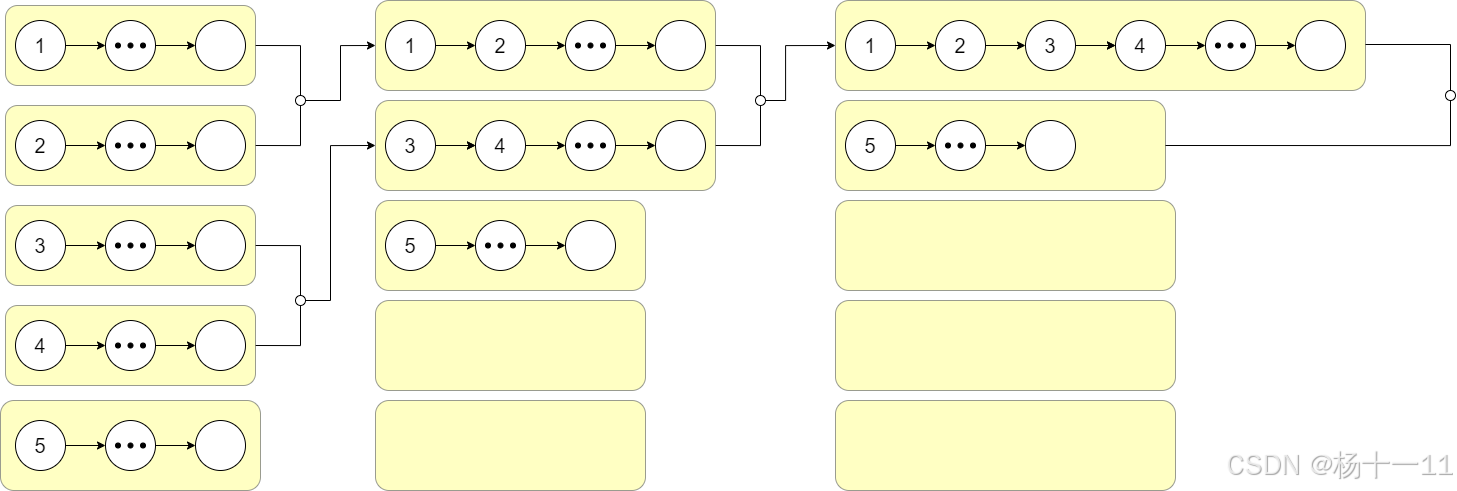
LeetCode热题100(三十四) —— 23.合并K个升序链表
LeetCode热题100(三十四) —— 23.合并K个升序链表 题目描述代码实现思路一:选择排序(199ms)思路二:归并排序(2ms) 思路解析 你好,我是杨十一,一名热爱健身的程序员在Coding的征程中,不断探索与…...

kalilinux - 目录扫描之dirsearch
情景导入 先简单介绍一下dirsearch有啥用。 假如你现在访问一个网站,例如https://www.example.com/ 它是一个电商平台或者其他功能性质的平台。 站在开发者的角度上思考,我们只指导https://www.example.com/ 但不知道它下面有什么文件,文…...

浅谈云计算04 | 云基础设施机制
探秘云基础设施机制:云计算的基石 一、云基础设施 —— 云计算的根基二、核心机制之网络:连接云的桥梁(一)虚拟网络边界ÿ…...

文件上传 分片上传
分片上传则是将一个大文件分割成多个小块分别上传,最后再由服务器合并成完整的文件。这种做法的好处是可以并行处理多个小文件,提高上传效率;同时,如果某一部分上传失败,只需要重传这一部分,不影响其他部分…...

【0391】Postgres内核 checkpointer process ① 启动初始化
相关文章: 【0108】checkpointer运行原理(概念篇)(1) 【0278】checkpointer 共享内存(CheckpointerShmem)初始化(3) 文章目录 1. 启动 checkpointer process1.1 初始化 checkpointer PID1.2 注册 signal1.3 初始化 last checkpoint time2. 确认 config 的 shared memo…...

链路追踪SkyWalking
链路追踪 链路追踪作用链路追踪的关键概念链路追踪的工作原理常用链路追踪工具链路追踪的实现步骤链路追踪的典型场景 SkyWalkingSkyWalking 的主要功能SkyWalking 的架构安装 SkyWalking从 SkyWalking 的官方 GitHub 仓库 下载最新版本。配置后端存储SkyWalking使用࿰…...

Uniapp判断设备是安卓还是 iOS,并调用不同的方法
在 UniApp 中,可以通过 uni.getSystemInfoSync() 方法来获取设备信息,然后根据系统类型判断当前设备是安卓还是 iOS,并调用不同的方法。 示例代码 export default {onLoad() {this.checkPlatform();},methods: {checkPlatform() {// 获取系…...

计算机网络 (42)远程终端协议TELNET
前言 Telnet(Telecommunication Network Protocol)是一种网络协议,属于TCP/IP协议族,主要用于提供远程登录服务。 一、概述 Telnet协议是一种远程终端协议,它允许用户通过终端仿真器连接到远程主机,并在远程…...

rtthread学习笔记系列-- 23 环形缓冲块 ringblock
文章目录 23 环形缓冲块 ringblock23.1 初始化23.2 PUT & GET 块23.3 块释放23.4 rt_rbb_blk_queue_get23.5 rt_rbb_blk_alloc https://github.com/wdfk-prog/RT-Thread-Study 23 环形缓冲块 ringblock 环形块状缓冲区简称为:rbb。与传统的环形缓冲区不同的是&…...

HunyuanVideo 文生视频模型实践
HunyuanVideo 文生视频模型实践 flyfish 运行 HunyuanVideo 模型使用文本生成视频的推荐配置(batch size 1): 模型分辨率(height/width/frame)峰值显存HunyuanVideo720px1280px129f60GHunyuanVideo544px960px129f45G 本项目适用于使用 N…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
