CF986 div2 ABCD补题

//***不知道在不在进步

A

注意点：其实这个暴力就行，但有个限制，就是最多走100遍如果不到那就一定到不了。其实我感觉10遍就可以了，但WA了。不管怎么说，100遍不超时而且稳对。

代码：

#include<bits/stdc++.h>
using namespace std;int t;
int n,a,b;
string s;int main()
{cin>>t;while(t--){cin>>n>>a>>b;int x=0,y=0,flag=0,g=0;cin>>s;for(int i=0;i<s.size();i++){if(g>n*100)break;if(s[i]=='N')y++;else if(s[i]=='E')x++;else if(s[i]=='S')y--;else x--;
//			cout<<x<<" "<<y<<" "<<g<<endl;if(x==a&&y==b){flag=1;break;}if(i==(s.size()-1))i=-1;g++;}if(flag==1){cout<<"YES\n";}else{cout<<"NO\n";}}return 0;
}

B

题目大意：n个数的等差数列，通过将其最大值不断取MEX，变成0 1 ... n-1的排列。

大体思路：这题其实不难想到通解，但是就是不成立的地方的特判有些细节要注意。先说通解的情况。如果b>0，那么这个排列本身就是递增的。那么只要我们每一次都变最后一位，那么一定可以将后面>n-1的全变为0~n-1范围内。接下来再考虑b=0的情况。一开始我以为只有bc都=0时才不行，但事实上b=0时c和n是有条件的。只有b==0&&n>c+2时才是不行的。

代码详解：

#include<iostream>
using namespace std;
#define int long long int t;
int n,b,c;//b:d   c:初始值signed main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>t;while(t--){cin>>n>>b>>c;if(b==0&&n>c+2){cout<<-1<<endl;continue;}else if(b==0){if(c<=n-1){cout<<n-1<<endl;}else{cout<<n<<endl;}}else{if(c>n-1){cout<<n<<endl;}else{cout<<n-((n-1-c)/b)-1<<endl;}}		}return 0;
}

C

代码：

#include<iostream>
using namespace std;
#define int long long int t,ans;
int n,m,v;
int a[1000010],pre[1000010],las[1000010],presum[1000010];int ef(int l,int r,int t){int mid,aa=-1;while(l<=r){mid=l+r>>1;if(las[mid]>=t){aa=mid;l=mid+1;}else{r=mid-1;}}return aa;
}signed main()
{cin>>t;while(t--){ans=0;cin>>n>>m>>v;for(int i=1;i<=n;i++){cin>>a[i];presum[i]=presum[i-1]+a[i];}int g=0;for(int i=1;i<=n;i++){g+=a[i];if(g>=v){pre[i]=pre[i-1]+1;g=0;}else{pre[i]=pre[i-1];}}g=0;for(int i=n;i>=1;i--){g+=a[i];if(g>=v){las[i]=las[i+1]+1;g=0;}else{las[i]=las[i+1];}}int flag=0;for(int i=1;i<=n;i++){int g=m-pre[i-1];int q=ef(i,n+1,g);
//			cout<<q<<endl;if(q==-1)continue;flag=1;ans=max(ans,presum[q-1]-presum[i-1]);}if(flag==0){cout<<-1<<endl;}else{cout<<ans<<endl;}}return 0;
}

D 

题目思路：首先，Alice只能从小的一步步往大的跳。我们可以考虑一种递推思路（也有点像dp?）画个图说明：

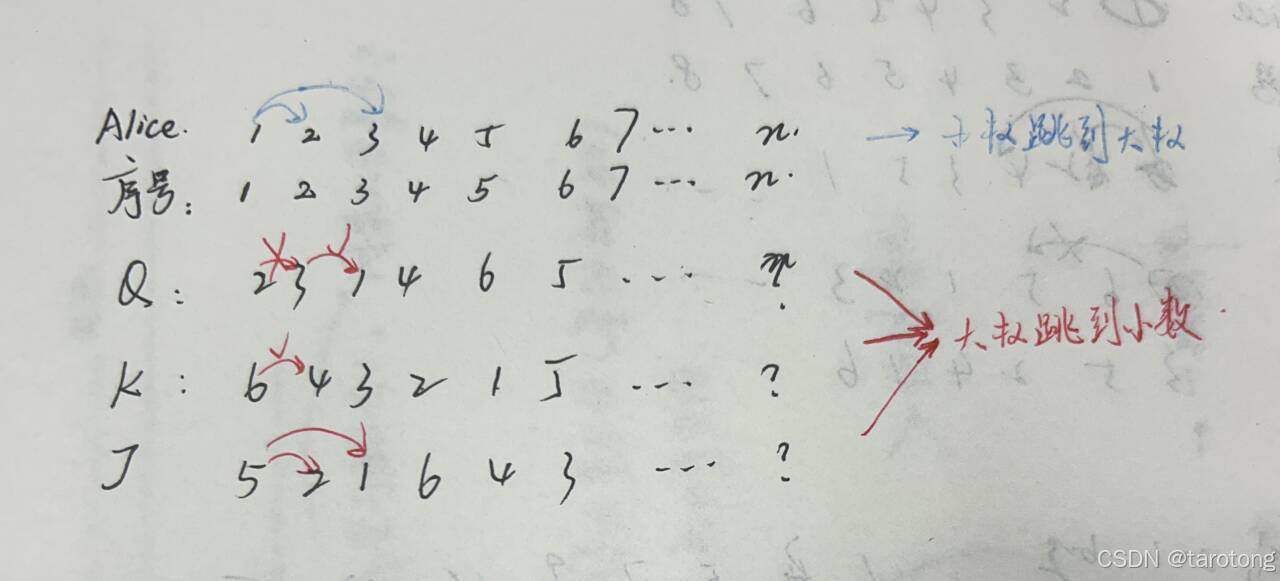
大概就是说，从1~n递推，每一位可以从其前面比它大的数得到。其实理解这个点之后题目就迎刃而解了。当然，记录输出的话，每一位记录一下其前面一个的字母和编号即可。用个递归输出。

代码：

#include<iostream>
using namespace std;
typedef pair<char,int>PII;int t,cnt;
int n;
int q[1000010],k[1000010],j[1000010];
PII ds[1000010];
pair<int,int>qm,km,jm;//qkj最大值的位置和大小;void print(int i){cnt++;if(ds[i].second==1){cout<<cnt<<endl;cout<<ds[i].first<<" "<<i<<endl;return ;}print(ds[i].second);cout<<ds[i].first<<" "<<i<<endl;
}int main()
{cin>>t;while(t--){cnt=0;cin>>n;ds[n].second=0;for(int i=1;i<=n;i++){cin>>q[i];}for(int i=1;i<=n;i++){cin>>k[i];}for(int i=1;i<=n;i++){cin>>j[i];}qm={1,q[1]};km={1,k[1]};jm={1,j[1]};for(int i=2;i<=n;i++){if(q[i]<qm.second){ds[i]={'q',qm.first};if(k[i]>km.second)km={i,k[i]};if(j[i]>jm.second)jm={i,j[i]};}else if(k[i]<km.second){ds[i]={'k',km.first};if(q[i]>qm.second)qm={i,q[i]};if(j[i]>jm.second)jm={i,j[i]};}else if(j[i]<jm.second){ds[i]={'j',jm.first};if(q[i]>qm.second)qm={i,q[i]};if(k[i]>km.second)km={i,k[i]};}}if(ds[n].second==0){cout<<"NO\n";}else{cout<<"YES\n";print(n);}}return 0;
}/*
3
1 2 3
1 3 2
1 2 3
*/

//同志仍需努力*****