动态规划(路径问题)
62. 不同路径
62. 不同路径 - 力扣(LeetCode)

动态规划思想第一步:描述状态~
dp[i][j]:表示走到i,j位置时,一共有多少种方法~
动态规划思想第二步:状态转移方程~

动态规划思想第三步:初始化(考虑边界情况)~


我们通过扩充数组大小可以节省初始化步骤,不过需要注意下标映射关系~
动态规划思想第四步:返回值~
return dp[m][n]
代码
//62 不同路径
class Solution
{
public:int uniquePaths(int m, int n){//创建dp表(注意扩充)vector<vector<int>> dp(m + 1, vector<int>(n + 1));//细节处理dp[0][1] = 1;//从起点开始填表for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){//状态转移方程dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}//返回值return dp[m][n];}
};其实动态规划核心就在于初始化和状态转移方程,之所以初始化主要考虑的就是填表边界情况,把特殊情况考虑了才方便让dp表一次到位。而状态转移方程尤其需要注意最近一步,一定得分析是如何到这一步的~
63. 不同路径 II
63. 不同路径 II - 力扣(LeetCode)

其实本道题跟上一道一样,唯一要注意的就是判定有无障碍物挡路~

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m+1,vector<int> (n+1));dp[0][1] = 1;for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){//小细节:dp表与原数组是对应不上的 if(obstacleGrid[i-1][j-1]==0){dp[i][j] = dp[i-1][j]+dp[i][j-1];}}}return dp[m][n];}
};代码就是在上一道题的基础上多了一步判断,由于我们的dp表与原数组不是同等大小了,所以要记得对应位置的映射。
LCR 166. 珠宝的最高价值
LCR 166. 珠宝的最高价值 - 力扣(LeetCode)

也练习挺多道的了,这道题甚至感觉不用画图,就照着前面的套路添加一个判断大小即可~
class Solution {
public:int jewelleryValue(vector<vector<int>>& nums) {//小case,直接秒杀int m = nums.size();int n = nums[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){dp[i][j] = nums[i-1][j-1]+max(dp[i-1][j],dp[i][j-1]);}}return dp[m][n];}
};931. 下降路径最小和
931. 下降路径最小和 - 力扣(LeetCode)



class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m = matrix.size();vector<vector<int>> dp(m+1,vector<int>(m+2,INT_MAX));for(int i = 0;i<=m+1;i++){dp[0][i] = 0;}for(int i = 1;i<=m;i++){for(int j = 1;j<=m;j++){dp[i][j] = min(dp[i-1][j],min(dp[i-1][j-1],dp[i-1][j+1]))+matrix[i-1][j-1];}}int ret = INT_MAX;for(int i = 1;i<=m;i++){ret = min(ret,dp[m][i]);}return ret;}
};64. 最小路径和
64. 最小路径和 - 力扣(LeetCode)


class Solution {
public:int minPathSum(vector<vector<int>>& grid) {//秒杀,分析越来越快了~int m = grid.size();int n = grid[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));dp[0][1] = 0;for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){dp[i][j] = min(dp[i][j-1],dp[i-1][j])+grid[i-1][j-1];}}return dp[m][n];}
};
174. 地下城游戏
174. 地下城游戏 - 力扣(LeetCode)


class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m = dungeon.size();int n = dungeon[0].size();vector<vector<int>> dp(m+1,vector(n+1,INT_MAX));dp[m][n-1] = dp[m-1][n] = 1;for(int i = m-1;i>=0;i--){for(int j = n-1;j>=0;j--){dp[i][j] = min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];dp[i][j] = max(1,dp[i][j]);}}return dp[0][0];}
};感觉讲得还不够好,不够详细,后面再作改善~
相关文章:

动态规划(路径问题)
62. 不同路径 62. 不同路径 - 力扣(LeetCode) 动态规划思想第一步:描述状态~ dp[i][j]:表示走到i,j位置时,一共有多少种方法~ 动态规划思想第二步:状态转移方程~ 动态规划思想第三步…...

python http调用视觉模型moondream
目录 一、什么是moondream 二、资源地址 三、封装了http进行接口请求 四、代码解析 解释 可能的改进 一、什么是moondream Moondream 是一个针对视觉生成任务的深度学习模型,专注于图像理解和生成,包括图像标注(captioning)、问题回答(Visual Question Answering,…...

Spark Streaming编程基础
文章目录 1. 流式词频统计1.1 Spark Streaming编程步骤1.2 流式词频统计项目1.2.1 创建项目1.2.2 添加项目依赖1.2.3 修改源目录1.2.4 添加scala-sdk库1.2.5 创建日志属性文件 1.3 创建词频统计对象1.4 利用nc发送数据1.5 启动应用,查看结果 2. 编程模型的基本概念3…...

深入 Flutter 和 Compose 的 PlatformView 实现对比,它们是如何接入平台控件
在上一篇《深入 Flutter 和 Compose 在 UI 渲染刷新时 Diff 实现对比》发布之后,收到了大佬的“催稿”,想了解下 Flutter 和 Compose 在 PlatformView 实现上的对比,恰好过去写过不少 Flutter 上对于 PlatformView 的实现,这次恰好…...

C# OpenCV机器视觉:红外体温检测
在一个骄阳似火的夏日,全球却被一场突如其来的疫情阴霾笼罩。阿强所在的小镇,平日里熙熙攘攘的街道变得冷冷清清,人们戴着口罩,行色匆匆,眼神中满是对病毒的恐惧。阿强作为镇上小有名气的科技达人,看着这一…...

FCA-FineDataLink认证
FCA-FineDataLink证书 Part.1:判断题 (总分:18分 得分:16) 第1题 判断题 数据同步只支持写入到已存在表,不支持自动建表(得分:2分 满分:2分) 正确答案:B 你的答案&…...

第19篇:python高级编程进阶:使用Flask进行Web开发
第19篇:python高级编程进阶:使用Flask进行Web开发 内容简介 在第18篇文章中,我们介绍了Web开发的基础知识,并使用Flask框架构建了一个简单的Web应用。本篇文章将深入探讨Flask的高级功能,涵盖模板引擎(Ji…...

js截取video视频某一帧为图片
1.代码如下 <template><div class"box"><div class"video-box"><video controls ref"videoRef" preload"true"src"https://qt-minio.ictshop.com.cn:9000/resource-management/2025/01/08/7b96ac9d957c45a…...

[云讷科技]Kerloud Falcon四旋翼飞车虚拟仿真空间发布
虚拟仿真环境作为一个独立的专有软件包提供给我们的客户,用于帮助用户在实际测试之前验证自身的代码,并通过在仿真引擎中添加新的场景来探索新的飞行驾驶功能。 环境要求 由于环境依赖关系,虚拟仿真只能运行在装有Ubuntu 18.04的Intel-64位…...

Jetson nano 安装 PCL 指南
本指南帮助 ARM64 架构的 Jetson Nano 安装 PCL(点云库)。 安装步骤 第一步:安装依赖 在终端中运行以下命令,安装 PCL 所需的依赖: sudo apt-get update sudo apt-get install git build-essential linux-libc-dev s…...

go-zero框架基本配置和错误码封装
文章目录 加载配置信息配置 env加载.env文件配置servicecontext 查询数据生成model文件执行查询操作 错误码封装配置拦截器错误码封装 接上一篇:《go-zero框架快速入门》 加载配置信息 配置 env 在项目根目录下新增 .env 文件,可以配置当前读取哪个环…...
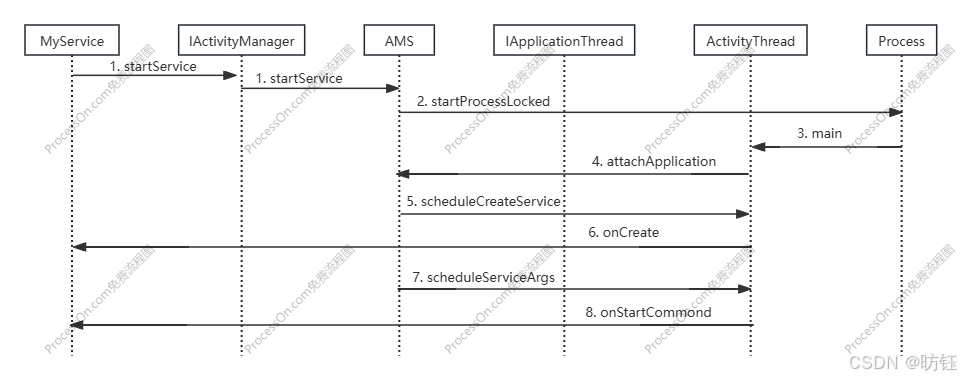
Android中Service在新进程中的启动流程2
目录 1、Service在客户端的启动入口 2、Service启动在AMS的处理 3、Service在新进程中的启动 4、Service与AMS的关系再续 上一篇文章中我们了解了Service在新进程中启动的大致流程,同时认识了与客户端进程交互的接口IApplicationThread以及与AMS交互的接口IActi…...
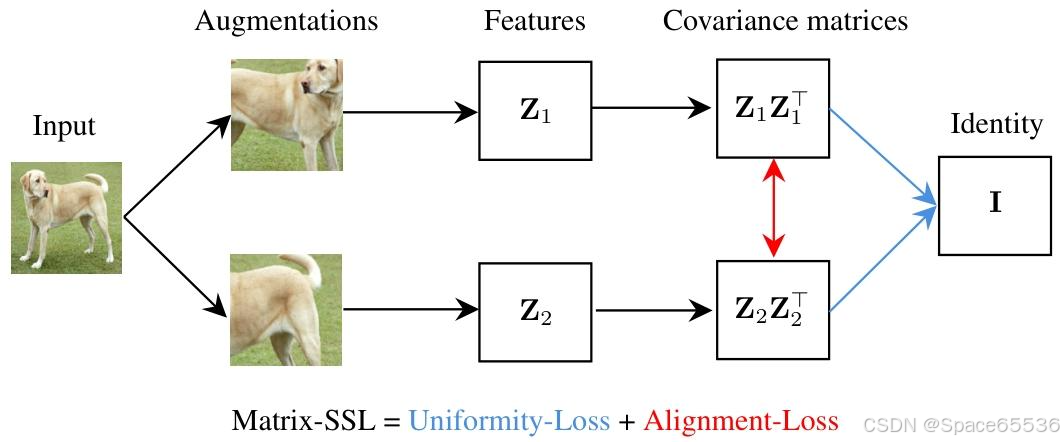
论文速读|Matrix-SSL:Matrix Information Theory for Self-Supervised Learning.ICML24
论文地址:Matrix Information Theory for Self-Supervised Learning 代码地址:https://github.com/yifanzhang-pro/matrix-ssl bib引用: article{zhang2023matrix,title{Matrix Information Theory for Self-Supervised Learning},author{Zh…...
)
ubunut22.04安装docker(基于阿里云 Docker 镜像源安装 Docker)
安装 更新包管理器: sudo apt update 安装 Docker 的依赖包 sudo apt install apt-transport-https ca-certificates curl gnupg lsb-release添加阿里云 Docker 镜像源 GPG 密钥: curl -fsSL https://mirrors.aliyun.com/docker-ce/linux/ubuntu/gp…...

k8s namespace绑定节点
k8s namespace绑定节点 1. apiserver 启用准入控制 PodNodeSelector2. namespace 添加注解 scheduler.alpha.kubernetes.io/node-selector3. label node 1. apiserver 启用准入控制 PodNodeSelector vim /etc/kubernetes/manifests/kube-apiserver.yaml spec:containers:- co…...
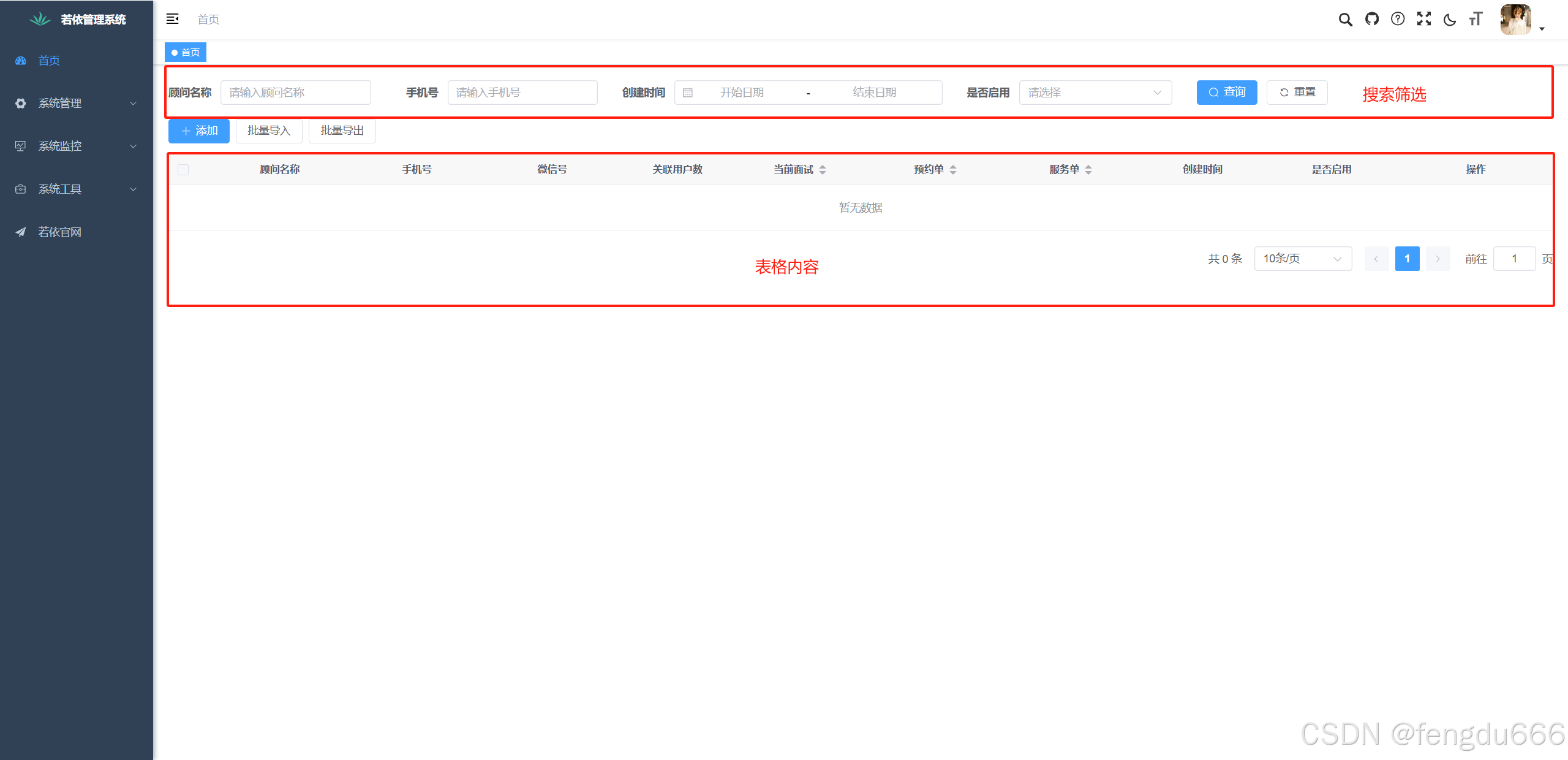
【ElementPlus】在Vue3中实现表格组件封装
预览 搜索筛选组件 <template><div><el-formref"formView":model"formData"label-width"auto"label-position"right":label-col-style"{ min-width: 100px }":inline"true"><el-form-item …...

cursor重构谷粒商城04——vagrant技术快速部署虚拟机
前言:这个系列将使用最前沿的cursor作为辅助编程工具,来快速开发一些基础的编程项目。目的是为了在真实项目中,帮助初级程序员快速进阶,以最快的速度,效率,快速进阶到中高阶程序员。 本项目将基于谷粒商城…...
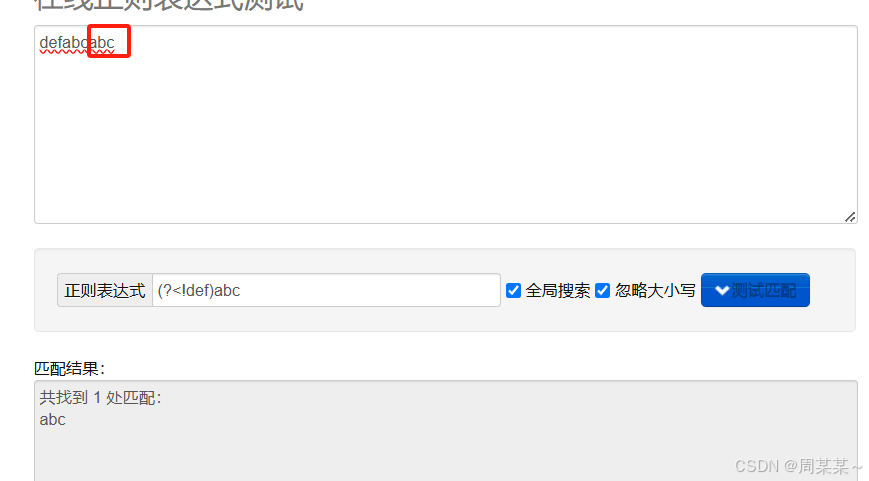
26、正则表达式
目录 一. 匹配字符 .:匹配除换行符外的任意单个字符。 二. 位置锚点 ^:匹配输入字符串的开始位置。 $:匹配输入字符串的结束位置。 \b:匹配单词边界。 \B:匹配非单词边界。 三. 重复限定符 *:匹配…...

SpringBoot使用MockMVC通过http请求controller控制器调用测试
说明 在Spring Boot中编写测试控制器调用是一个常见的需求,通常使用Spring的测试框架来完成。Spring Boot提供了多种方式来测试控制器,包括使用MockMvc进行模拟HTTP请求和响应的测试。 基本示例 1. 创建Spring Boot项目 首先,确保你已经创建了一个Spring Boot项目。如果…...
【Unity3D】Unity混淆工具Obfuscator使用
目录 一、导入工具 二、各种混淆形式介绍 2.1 程序集混淆 2.2 命名空间混淆 2.3 类混淆 2.4 函数混淆 2.5 参数混淆 2.6 字段混淆 2.7 属性混淆 2.8 事件混淆 三、安全混淆 四、兼容性处理 4.1 动画方法兼容 4.2 GUI方法兼容 4.3 协程方法兼容 五、选项 5.1 调…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
