AF3 FourierEmbedding类源码解读
FourierEmbedding 是一个用于扩散条件的傅里叶嵌入类,其核心是将输入的时间步噪声强度或控制参数(timestep)转换为高维的周期性特征。
源代码:
class FourierEmbedding(nn.Module):"""Fourier embedding for diffusion conditioning."""def __init__(self, embed_dim):super(FourierEmbedding, self).__init__()self.embed_dim = embed_dim# Randomly generate weight/bias once before trainingself.weight = nn.Parameter(torch.randn((1, embed_dim)))self.bias = nn.Parameter(torch.randn((1, embed_dim)))def forward(self, t):"""Compute embeddings"""two_pi = torch.tensor(2 * 3.1415, device=t.device, dtype=t.dtype)return torch.cos(two_pi * (t * self.weight + self.bias))类代码解读:
1. 类的功能
该模块的主要目的是通过傅里叶变换,将输入的时间步嵌入到一个周期性的高维特征空间。这种处理方式在扩散模型中尤为重要,因为时间步本身是一个标量(单一数值),通过傅里叶嵌入,模型能够更好地捕获时间的周期性模式。
2. __init__ 方法
def __init__(self, embed_dim):super(FourierEmbedding, self).__init__()self.embed_dim = embed_dim# Randomly generate weight/bias once before trainingself.weight = nn.Parameter(torch.randn((1, embed_dim)))self.bias = nn.Parameter(torch.randn((1, embed_dim)))
功能
- 初始化傅里叶嵌入模块。
- 生成随机初始化的权重和偏置(
weight和bias),用于控制傅里叶变换的频率和相位。
重要参数
embed_dim:- 表示嵌入的维度,即输出特征的大小。
- 在扩散模型中,较大的
e
相关文章:

AF3 FourierEmbedding类源码解读
FourierEmbedding 是一个用于扩散条件的傅里叶嵌入类,其核心是将输入的时间步噪声强度或控制参数(timestep)转换为高维的周期性特征。 源代码: class FourierEmbedding(nn.Module):"""Fourier embedding for diffusion conditioning."""de…...

vsftpd虚拟用户部署
vsftpd虚拟用户部署 案例提供两个用户如下,使用centos7验证可行。 test *AO9ih&7 ftp DTx4zp_shell脚本运行一键安装vsftp #!/bin/bash yum -y install vsftpd ftp >/etc/vsftpd/vsftpd.conf cat <<EOL >> /etc/vsftpd/vsftpd.conf anonymous_enableNO l…...

MySQL 容器已经停止(但仍然存在),但希望重新启动它,并使它的 3306 端口映射到宿主机的 3306 端口是不可行的
重新启动容器并映射端口是不行的 由于你已经有一个名为 mysql-container 的 MySQL 容器,你可以使用 docker start 启动它。想要让3306 端口映射到宿主机是不行的,实际上,端口映射是在容器启动时指定的。你无法在容器已经创建的情况下直接修改…...

汇编实验·顺序程序设计
一、实验目的: 1.能够熟练的进行顺序程序的编写,掌握基本的汇编语言指令的用法 2.通过程序设计理解掌握不同类型的数据混合运算的基本规则 3.熟练掌握各种寻址方式,深入理解逻辑地址和物理地址的相关概念 二、实验内容 有三个长度分别为1、2、4个字节的数据,编写程序求…...

AIGC视频扩散模型新星:Video 版本的SD模型
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文详细介绍慕尼黑大学携手 NVIDIA 等共同推出视频生成模型 Video LDMs。NVIDIA 在 AI 领域的卓越成就家喻户晓,而慕尼黑大学同样不容小觑,…...

HarmonyOS:通过(SQLite)关系型数据库实现数据持久化
一、场景介绍 关系型数据库基于SQLite组件,适用于存储包含复杂关系数据的场景,比如一个班级的学生信息,需要包括姓名、学号、各科成绩等,又或者公司的雇员信息,需要包括姓名、工号、职位等,由于数据之间有较…...

10. SpringCloud Alibaba Sentinel 规则持久化部署详细剖析
10. SpringCloud Alibaba Sentinel 规则持久化部署详细剖析 文章目录 10. SpringCloud Alibaba Sentinel 规则持久化部署详细剖析1. 规则持久化1.1 Nacos Server 配置中心-规则持久化实例 2. 最后: 1. 规则持久化 规则没有持久化的问题 如果 sentinel 流控规则没有…...

STM32更新程序OTA
STM32的OTA(Over-The-Air)更新程序是一种通过无线通信方式,为设备分发新软件、配置甚至更新加密密钥的技术。以下是关于STM32 OTA更新程序的详细介绍: 一、OTA升级流程 STM32的OTA升级流程通常包括以下几个关键步骤:…...
|稀土掘金-147.寻找独一无二的糖葫芦串、119.游戏队友搜索)
MarsCode青训营打卡Day10(2025年1月23日)|稀土掘金-147.寻找独一无二的糖葫芦串、119.游戏队友搜索
资源引用: 147.寻找独一无二的糖葫芦串 119.游戏队友搜索 今日小记: 回乡聚会陪家人,休息一天~ 稀土掘金-147.寻找独一无二的糖葫芦串(147.寻找独一无二的糖葫芦串) 题目分析: 给定n个长度为m的字符串表…...
 : 安装组件出错解决)
vue(33) : 安装组件出错解决
1. request to https://registry.npm.taobao.org/semver/download/semver-6.1.1.tgz?cache0&other_urlshttps%3A%2F%2Fregistry.npm.taobao.org%2Fsemver%2Fdownload%2Fsemver-6.1.1.tgz failed, reason: certificate has expired 这个错误提示表明你在尝试从https://reg…...

ChatGPT结合Excel辅助学术数据分析详细步骤分享!
目录 一.Excel在学术论文中的作用✔ 二.Excel的提示词✔ 三. 编写 Excel 命令 四. 编写宏 五. 执行复杂的任务 六. 将 ChatGPT 变成有用的 Excel 助手 一.Excel在学术论文中的作用✔ Excel作为一种广泛使用的电子表格软件,在学术论文中可以发挥多种重要作用&a…...
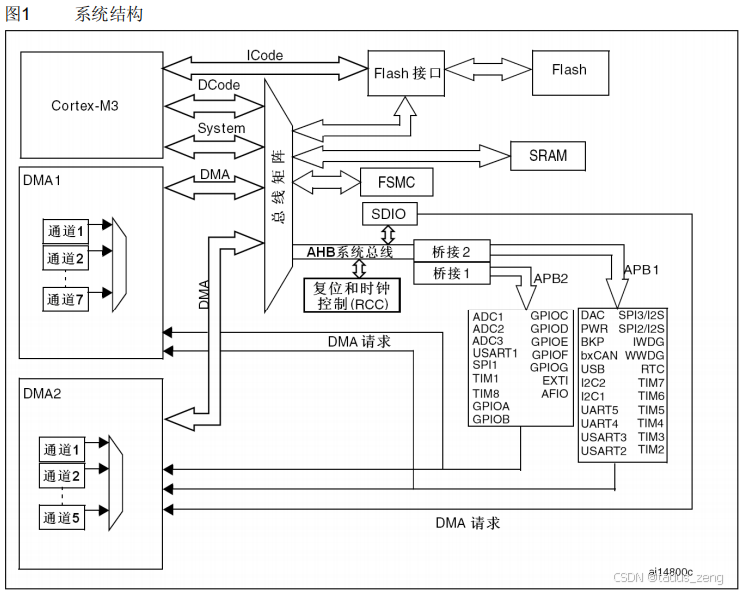
stm32f103 单片机(一)第一个工程
先看一个简单的 系统上已经安装好了keil5 与ARM包,也下载好了STM32固件库 新建一个工程,添加三个组 加入如下文件 在options 里作如下配置 准备在main.c 中写下第一个实验,点亮一个小灯。 像51单片机一样直接对引脚赋值是行不通的 在…...
云计算和服务器
一、云计算概述 ICT是世界电信协会在2001年的全球性会议上提出的综合性概念,ICT分为IT和CT,IT(information technology)信息技术,负责对数据生命周期的管理;CT(communication technology),负责数据的传输管理。 CT技术…...
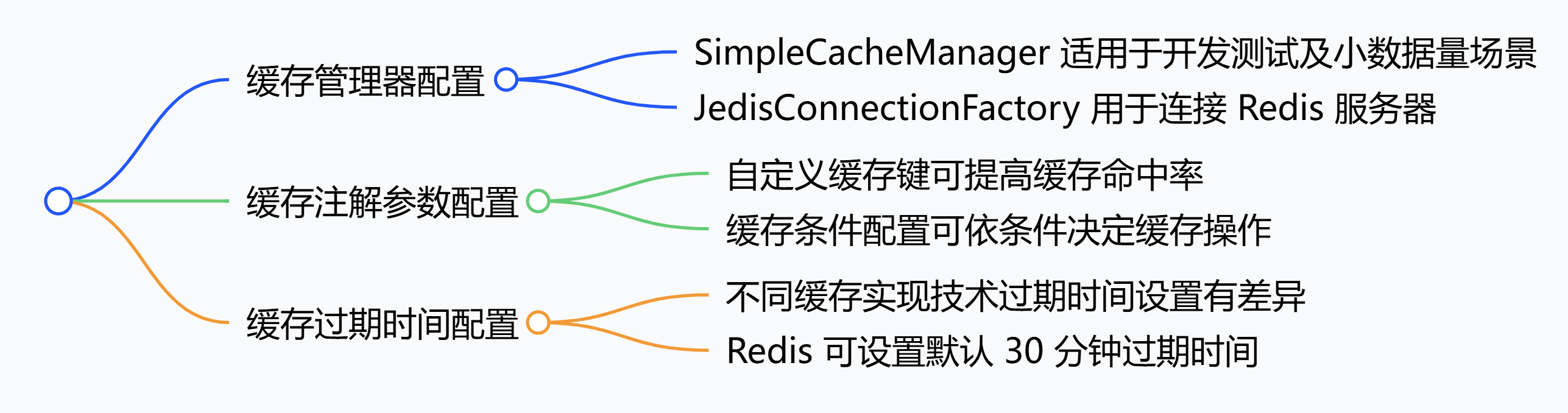
Spring 框架:配置缓存管理器、注解参数与过期时间
在 Spring 框架中,可通过多种方式配置缓存具体行为,常见配置方法如下。 1. 缓存管理器(CacheManager)配置 基于内存的缓存管理器配置(以SimpleCacheManager为例) SimpleCacheManager 是 Spring 提供的简单…...
Linux系统 C/C++编程基础——基于Qt的图形用户界面编程
ℹ️大家好,我是练小杰,今天周四了,距离除夕只有4天了,各位今年卫生都搞完了吗!😆 本文是接着昨天Linux 系统C/C编程的知识继续讲,基于Qt的图形用户界面编程概念及其命令,后续会不断…...

并发编程 - 线程同步(一)
经过前面对线程的尝试使用,我们对线程的了解又进一步加深了。今天我们继续来深入学习线程的新知识 —— 线程同步。 01、什么是线程同步 线程同步是指在多线程环境下,确保多个线程在同时使用共享资源时不会发生冲突或数据不一致问题的技术,保…...

PyTorch入门 - 为什么选择PyTorch?
PyTorch入门 - 为什么选择PyTorch? Entry to PyTorch - Why PyTorch? by JacksonML $ pip install pytorch安装完毕后,可以使用以下命令,导入第三方库。 $ import pytorch...
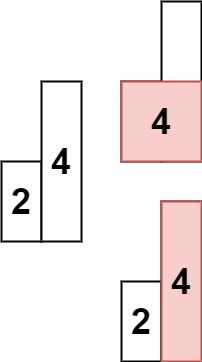
leetcode刷题记录(八十六)——84. 柱状图中最大的矩形
(一)问题描述 84. 柱状图中最大的矩形 - 力扣(LeetCode)84. 柱状图中最大的矩形 - 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾…...

Android GLSurfaceView 覆盖其它控件问题 (RK平台)
平台 涉及主控: RK3566 Android: 11/13 问题 在使用GLSurfaceView播放视频的过程中, 增加了一个播放控制面板, 覆盖在视频上方. 默认隐藏setVisibility(View.INVISIBLE);点击屏幕再显示出来. 然而, 在RK3566上这个简单的功能却无法正常工作. 通过缩小视频窗口可以看到, 实际…...
开源鸿蒙开发者社区记录
lava鸿蒙社区可提问 Laval社区 开源鸿蒙项目 OpenHarmony 开源鸿蒙开发者论坛 OpenHarmony 开源鸿蒙开发者论坛...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
