Ansys Speos | Speos Meshing 网格最佳实践
概述
网格划分是在各种计算应用中处理3D几何的基本步骤:
-
表面和体积:网格允许通过将复杂的表面和体积分解成更简单的几何元素(如三角形、四边形、四面体或六面体)来表示复杂的表面和体积。
-
模拟和渲染:网格是创建离散域的关键。这个领域用于数值模拟,允许模拟物理现象,如应力分布、传热、流体流动,以及光学几何界面上的折射、衍射、散射。
-
计算机辅助设计(CAD):在CAD系统中使用网格来表示三维模型和曲面。在设计过程中,CAD模型经常使用网格来有效地存储、操作和可视化几何信息。下面是一个用网格制作的汽车前部的例子,用简单的元素构建复杂的形状。

总体介绍
在计算机图形学和计算几何中,3D网格是指定义三维对象的形状和结构的节点、边和面的集合,网格划分是创建这种表征的过程,它包括将3D空间划分为离散的元素,以近似目标的几何形状。3D网格的一些关键项:
-
节点(或顶点):在3D空间中定义网格元素角的点。
-
边(或线):连接顶点并形成网格元素的边界。
-
面(或多边形):由边缘闭合环定义的平面,在3D网格中,面通常是三角形或四边形。
网格划分需确定如何分布节点并将它们连接起来以形成近似被建模对象形状的元素。

在Speos中使用网格
Speos使用网格划分来生成几何的离散元素。Speos基于三角形曲面网格划分,该方法在计算机辅助设计(CAD)软件中得到了广泛应用。由于Speos可以嵌入到各种CAD环境中,它依赖于来自CAD的网格算法。这意味着,相同的网格值,网格表现从一个CAD平台到另一个CAD平台是不同的。
Speos使用表面网格而不是体积网格,因为面网格比体积网格算法更容易管理,为大型和复杂的几何图形提供了更好的分析效率。
1.Speos网格参数
有两种方式编辑Speos网格参数。通过模拟(正向,逆向,交互式)选项,或通过局部网格定义。这两个选项依赖于相同的参数,仿真选项中的参数影响在仿真中分配的所有几何形状。局部网格定义中的参数只影响分配给它的几何形状或面。这些参数优先于仿真参数中指定的一般网格参数。

2.参数
参数化网格的方法有三种:
-
SAG:控制表面网格和几何形状。Sag对应于一个表面偏差。它适用于面或边缘弯曲的情况。当面为平面且所有边均为直线时,Sag无作用。

-
Step:控制三角网格段的长度。Step对应于网格最大边缘长度。较小的网格Step值生成的三角形具有较小的边缘长度,这会增加结果的准确性。
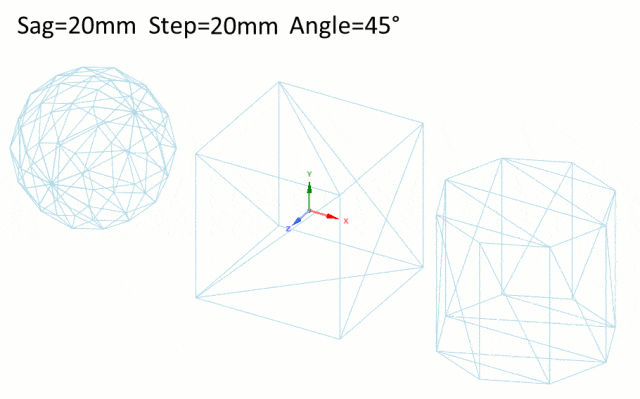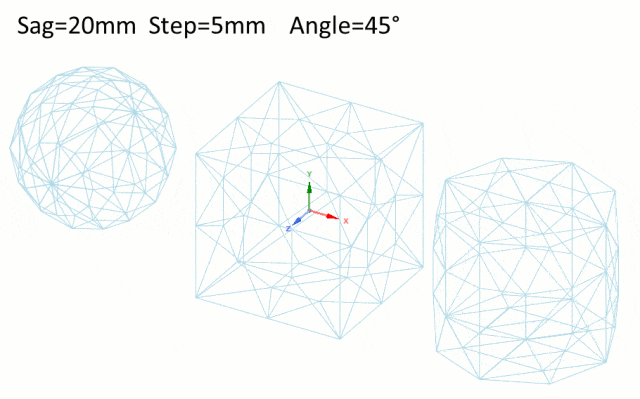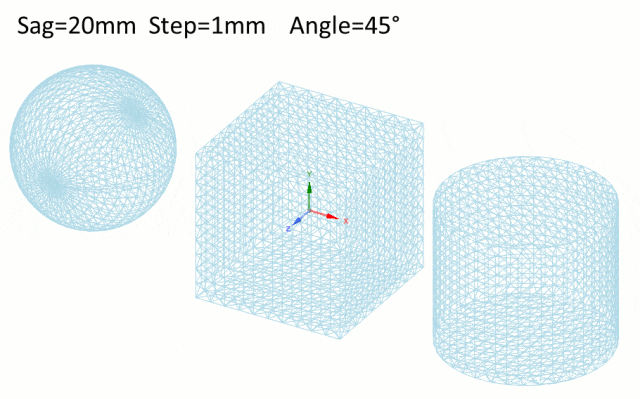
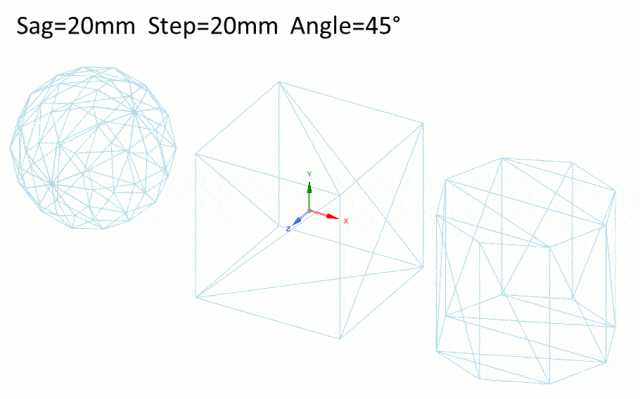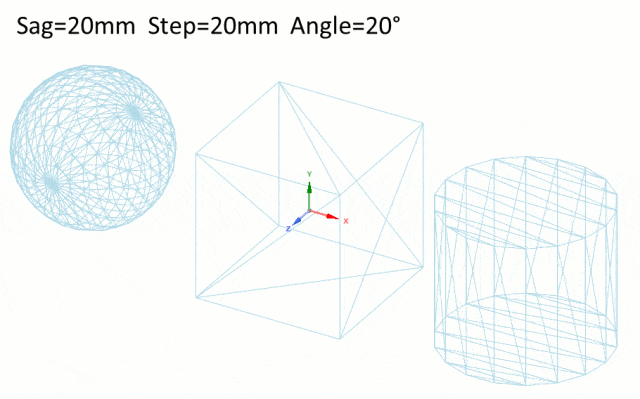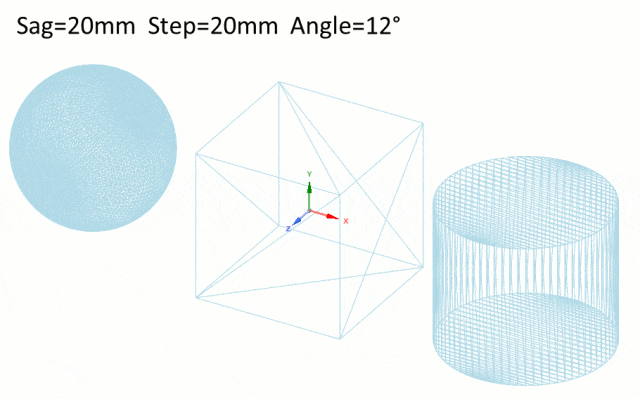
-
Angle角度:角度控制网格三角形所有法线的最大角度公差。从理论上讲,当表面是弯曲的时候,角度越小,三角形就越小。
3.Meshing模式
Speos提供了三种网格模式,它们决定几何图形如何网格化,适用于SAG公差和Step步长。
-
Proportional to face,与face面成比例,调整对象的每个面的大小。

其中,Length长度值对应于面边界框(下图中蓝色突出显示的正方形)的对角线长度。
SAG值是用户作为输入参数提供的值。
![]()
|
| 优点: 多线程 可能在特定区域获得更好的分辨率网格。 与每个面成比例的Sag/Step。 网格需要的面,可用于非流形面/对象(独立面/分割面) 缺点: 网孔不水密(不完全闭合)的风险 |
-
Proportional to body,与body 体成比例,调整到对象体的大小。
![]()
其中,Length长度对应于Body Bounding Box(下图中蓝色突出显示的平行六面体)的对角线长度。
SAG值是用户作为输入参数提供的值。
![]()
|
| 优点: Sag/Step与body体成正比 水密网格 比Fixed模式的点/边更少,性能更好 缺点: 不是多线程 有可能得到一个粗糙的网格警告,需要进一步局部网格划分 |
-
Fixed固定,无论物体的大小或形状如何,网格大小都保持不变。
|
| 优点: 简单的网格 水密网格 缺点: 不是多线程 比Propertional to body 有更多的点/边 需要更多的RAM资源 |
水密性原则
“水密”一词传达的意思是网是完全封闭的,就像一个水密容器。实际上,水密网格可以确保模型中没有开放的表面或缝隙,这对于精确的物理模拟和逼真的渲染非常重要。
当网格元素(面、段和节点)之间没有间隙或重叠时,网格被认为是水密的。下面是快速诊断的可视化:
-
如果是:网格是水密(右图)
-
缩放敏感对象区域(如边缘或角落)的3D视图。
-
激活预览网格(右键单击在模拟或局部网格中选择的物体/面)
-
检查局部三角形是否在面的边缘/角上公共节点。
-
如果没有:网格不水密(左图)
-
| Non-watertight mesh | Watertight mesh |
|
|
|
在Speos中使用非水密网格的常见后果是模拟期间的高错误率。当网格中有孔洞时,射线通过孔洞传播,直接归类为误差射线。可以在模拟运行期间或在模拟完成后生成的HTML报告中看到错误百分比。
常见的网格警告
识别警告信息并了解它们的来源,当speos未能应用用户定义的网格时,在模拟初始化阶段出现网格警告信息。有两种警告类型:
|
| 当某些面用较粗的网格参数进行网格划分时出现。 |
|
| 当某些面根本没有网格化时出现。 |
下面的工作流程解释了这些消息是如何出现的以及出现的原因:

在此基础上分析太小而不能网格化的面,双击警告可以选择受网格影响的所有面,使用以下工具选择定位这些face的位置:
-
复制/粘贴到结构树(Ctrl + C和Ctrl + V)。
-
创建一个群组group,并将其扩展到群组。
-
分析face:
- 使用spaceclaim测量工具。不正确的面可能导致一条线或一个区域具有非正值。
- 使用Check Geometry 选项(仅用于复制/粘贴选项)来查找自相交,拓扑错误,…

网格划分最佳实践
网格划分是模拟模型的关键步骤,花时间在复杂几何形状的模型上,找到好的网格参数是很重要的。如果没有高质量的几何图形作为输入,meshing性能和精度就无法达到最佳。在进行任何网格划分操作之前,请确保按预期导入几何图形。Ansys建议在将其导入Speos之前检查CAD几何形状的质量。一些软件编辑提出了专门用于确保CAD数据质量的工具。
3D表面网格划分指南,考虑以下几点在3D表面上有效的网格划分:
-
三角形质量和宽高比:确保三角形网格元素质量好,并尊重平衡的比例,避免高度扭曲的元素。
-
三角形尺寸渐变:在关键区域逐渐改变网格元素的大小。在复杂的几何形状或高梯度的区域可能需要更细的网格,而在更均匀的区域可以使用更粗的网格,以减少计算成本。
-
网孔密度控制:根据需要控制网格密度。
在复杂的几何形状或复杂大模型情况下,花时间在网格定义上通常可以保证一个好的模型网格,但是这会给剩下的仿真模拟计算部分带来额外的时间。复杂的几何形状(例如球形)中,更精细的网格划分需要更多的三角形;这意味着初始化时间增加了。如果多次迭代模拟以进行扫描参数或初始优化,则使用更粗的网格可能更有效。另一种方法是使用LightBox,将网格体现在lightbox中,在仿真中调用lightbox。
实用的建议
充分利用局部网格,局部网格是一种将特定网格参数“强制”到一组,当一个局部网格应用于一个面,在仿真模拟过程中,Speos将对这组面考虑局部网格属性,而不是全局网格属性(设置在模拟的选项)。局部网格的主要优点是通过提高光路中重要的特定元素的网格精度,为模型带来准确性。
局部网格还能够驱动3D辐照度传感器的分辨率。为了获得均匀一致的分辨率,建议在Fixed模式下使用Step参数。

由于局部网格可能会在网格上产生非水密行为,建议这样设置:
-
在模拟选项中微调全局网格设置-注意创建的每个模拟都有独立的网格参数。如果希望在不同的模拟中使用相同的网格设置,请通过复制和粘贴simulation来复制现有的模拟网格设置。
-
在被光线击中的概率相对较低的几何体上创建一个或几个粗糙的局部网格。
-
为3D传感器创建特定的局部网格。注意一个面不能链接到多个局部网格。
ODX文件导入-应用网格类型
Speos 2024R1版本,针对lens 系统,可以通过Speos ODX工具从OpticStudio导入几何图形。导入的数据有两种元素:
第一是在结构树下的CAD几何图形。
第二是在组件中的网格几何形状。组件中的网格几何必须用于模拟,它们也有自己的网格属性。可以通过右键单击>选项访问它们。
|
|
|
在2024R1中,没有可用的预览网格。如果默认参数不能提供所需的精度,请尝试以下设置:

在2024R2及以后,预览网格是可用的。
相关文章:

Ansys Speos | Speos Meshing 网格最佳实践
概述 网格划分是在各种计算应用中处理3D几何的基本步骤: 表面和体积:网格允许通过将复杂的表面和体积分解成更简单的几何元素(如三角形、四边形、四面体或六面体)来表示复杂的表面和体积。 模拟和渲染:网格是创建离散…...

elasticsearch segment数量对读写性能的影响
index.merge.policy.segments_per_tier 是一个配置选项,用于控制 Elasticsearch 中段(segment)合并策略的行为。它定义了在每一层的段合并过程中,允许存在的最大段数量。调整这个参数可以优化索引性能和资源使用。 假设你有一个索…...

全同态加密理论、生态现状与未来展望(中2)
《全同态加密理论、生态现状与未来展望》系列由lynndell2010gmail.com和mutourend2010gmail.com整理原创发布,分为上中下三个系列: 全同态加密理论、生态现状与未来展望(上):专注于介绍全同态加密理论知识。全同态加密…...
鸿蒙UI(ArkUI-方舟UI框架)-开发布局
返回主章节 → 鸿蒙UI(ArkUI-方舟UI框架) 开发布局 1、布局概述 1)布局结构 2)布局元素组成 3)如何选择布局 声明式UI提供了以下10种常见布局,开发者可根据实际应用场景选择合适的布局进行页面开发。 …...
RPC是什么?和HTTP区别?
RPC 是什么?HTTP 是什么? 作为一个程序员,假设我们需要从A电脑的进程发送一段数据到B电脑的进程,我们一般会在代码中使用 Socket 进行编程。 此时,可选性一般就是 TCP 和 UDP 二选一,由于 TCP 可靠、UDP 不…...

Linux C\C++编程-建立文件和内存映射
【图书推荐】《Linux C与C一线开发实践(第2版)》_linux c与c一线开发实践pdf-CSDN博客 《Linux C与C一线开发实践(第2版)(Linux技术丛书)》(朱文伟,李建英)【摘要 书评 试读】- 京东图书 Linu…...
行政纠错——pycorrector学习
pycorrector是一个开源中文文本纠错工具,它支持对中文文本进行音似、形似和语法错误的纠正。此工具是使用Python3进行开发的,并整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer等多种模型来实现文本纠错功能。pycorrector官方仓库…...

Go的defer原理
Go 的 defer 原理 defer 是 Go 语言中的一个关键字,用于延迟执行一个函数调用。它通常用于处理资源释放、连接关闭等操作,确保这些操作在函数返回之前执行。 1. 什么是 defer? defer 关键字用于延迟执行一个函数调用,直到包含它…...

Windows 下本地 Docker RAGFlow 部署指南
Windows 下本地 Docker RAGFlow 部署指南 环境要求部署步骤1. 克隆代码仓库2. 配置 Docker 镜像加速(可选)3. 修改端口配置(可选)4. 启动服务5. 验证服务状态6. 访问服务7. 登录系统8. 配置模型8.1 使用 Ollama 本地模型8.2 使用在线 API 服务9. 开始使用10. 常见问题处理端…...

专题三_穷举vs暴搜vs深搜vs回溯vs剪枝_全排列
dfs解决 全排列&子集 1.全排列 link:46. 全排列 - 力扣(LeetCode) 全局变量回溯 code class Solution { public:vector<vector<int>> ans;vector<int> cur;vector<bool> used;vector<vector<int>> permute…...

【IEEE Fellow 主讲报告| EI检索稳定】第五届机器学习与智能系统工程国际学术会议(MLISE 2025)
重要信息 会议时间地点:2025年6月13-15日 中国深圳 会议官网:http://mlise.org EI Compendex/Scopus稳定检索 会议简介 第五届机器学习与智能系统工程国际学术会议将于6月13-15日在中国深圳隆重召开。本次会议旨在搭建一个顶尖的学术交流平台…...

华为E9000刀箱服务器监控指标解读
美信监控易内置了数千种常见设备监测器,能够监测超过20万项指标。这些指标涵盖了从硬件设备到软件系统,从网络性能到安全状态等各个方面。如下基于美信监控易——IT基础监控模块,对华为E9000刀箱服务器部分监控指标进行解读。 一、华为E9000…...

【LC】2544. 交替数字和
题目描述: 给你一个正整数 n 。n 中的每一位数字都会按下述规则分配一个符号: 最高有效位 上的数字分配到 正 号。剩余每位上数字的符号都与其相邻数字相反。 返回所有数字及其对应符号的和。 示例 1: 输入:n 521 输出&…...
QT QTreeWidget控件 全面详解
本系列文章全面的介绍了QT中的57种控件的使用方法以及示例,包括 Button(PushButton、toolButton、radioButton、checkBox、commandLinkButton、buttonBox)、Layouts(verticalLayout、horizontalLayout、gridLayout、formLayout)、Spacers(verticalSpacer、horizontalSpacer)、…...
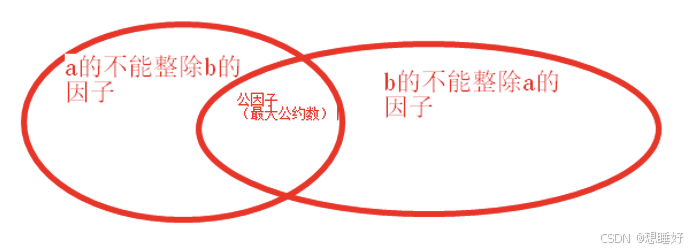
欧几里得算法求最小公倍数和最大公约数
一.最大公约数 gcd(a,b)gcd(b,a%b) 递归式,当且仅当b0,易得0和a的公约数为a.(可作为递归的出口) 证明: int gcd(int a, int b) {if (b 0) return a;else return gcd(b, a % b); } 二.最小公倍数 给定整数a b,求a b的最小公倍数 有图可知…...

Selenium配合Cookies实现网页免登录
文章目录 前言1 方案一:使用Chrome用户数据目录2 方案二:手动获取并保存Cookies,后续使用保存的Cookies3 注意事项 前言 在进行使用Selenium进行爬虫、网页自动化操作时,登录往往是一个必须解决的问题,但是Selenium每次…...
DeepSeek R1模型解读与使用
字节在春节前发布了doubao-1.5,它的官方介绍竟然是这样的: 这次发布了四个型号,doubao-1.5-pro-32k, doubao-1.5-pro-256k, doubao-1.5-lite-32k, doubao-1.5-vision-pro-32k,价格全部与上一个版本doubao模型一致,加量…...

Windows电脑不小心点击了关机,关机过程中如何阻止
如果电脑正在关机的过程中,想要阻止关机,可以尝试以下方法: 如果关机过程较慢,可以按下键盘组合键 Win R 打开运行窗口。输入 shutdown -a 后按回车键,这将中断关机操作(适用于 Windows 系统)…...
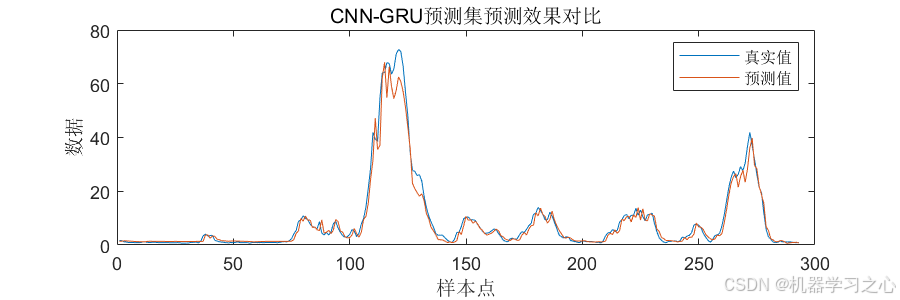
CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据)
CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据) 目录 CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据)预测效果基本介绍CNN-GRU卷积门控循环单元时间序列预测一、引言1.1、研究背景与意义1.2、研究现状1…...

【吉林乡镇界】面图层shp格式arcgis数据乡镇名称和编码wgs84无偏移内容测评
标题中的“吉林省乡镇界面图层shp格式arcgis数据乡镇名称和编码wgs84无偏移”揭示了这是一个地理信息系统(GIS)相关的数据集,主要用于描绘吉林省的乡镇边界。这个数据集包含了一系列的文件,它们是ArcGIS软件能够识别和处理的Shape…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...









