机器学习:支持向量机
支持向量机(Support Vector Machine)是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的广义线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。

假设两类数据可以被 H = x : w T x + b ≥ c H = {x:w^Tx + b \ge c} H=x:wTx+b≥c分离,垂直于法向量 w w w,移动 H H H直到碰到某个训练点,可以得到两个超平面 H 1 H_1 H1和 H 2 H_2 H2,两个平面称为支撑超平面,题目分别支撑两类数据。而位于 H 1 H_1 H1和 H 2 H_2 H2正中间的超平面是分离这两类数据的最好选择。支持向量就是离分隔超平面最近的那些点。
法向量 w w w有很多种选择,超平面 H 1 H_1 H1和 H 2 H_2 H2之间的距离称为间隔,这个间隔是 w w w的函数,**目的就是寻找这样的 w w w使得间隔达到最大。




在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。
-
拉格朗日乘子法
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,可将有 d d d个变量与 k k k个约束条件的最优化问题转化为具有 d + k d+k d+k个变量的无约束优化问题求解。
-
二次规划
二次规划是一类典型的优化问题,包括凸二次优化和非凸二次优化。在此类问题中,目标函数是变量的二次函数,而约束条件是变量的线性不等式。
m i n 1 2 x T Q x + c T x s . t . A ⃗ x ⃗ ≤ b ⃗ min \frac{1} {2} x^T Q x + c^T x \\ s.t. \vec{A} \vec{x} \le \vec{b} min21xTQx+cTxs.t.Ax≤b
具体公式证明:【整理】深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件 - mo_wang - 博客园 (cnblogs.com)
序列最小优化(Sequential Minimal Optimization,SMO)
序列最小优化是将大优化问题分界成多个小优化问题来求解。
SMO算法工作原理:每次循环中选择两个变量进行优化处理。一旦找到一对合适的变量,那么就增大其中一个同时减小另一个。这里的“合适”指的是两个变量必须要符合一定的条件,条件之一就是这两个变量必须要在间隔边界之外,而其第二个条件则是这两个变量还没有进行过区间化处理或者不在边界上。

代码实现
参考《机器学习实战》,代码链接:https://github.com/golitter/Decoding-ML-Top10/tree/master/SVM
这里采用简化的SMO代码,数据集是https://blog.caiyongji.com/assets/mouse_viral_study.csv。
data_processing.py:
import numpy as np
import pandas as pd# https://zhuanlan.zhihu.com/p/350836534
def data_processing():data_csv = pd.read_csv('mouse_viral_study.csv')data_csv = data_csv.dropna()# print(data_csv)X = data_csv.iloc[:-1, 0:2].values# print(X)Y = data_csv.iloc[:-1, 2].map({0: -1, 1: 1}).valuesY = Y.reshape(-1, 1)# print(Y.shape)return X, Y# X, Y = data_processing()
# print(X)
工具模块,smo_assist.py:
import random
def select_Jrandom(i:int, m:int) -> int:"""随机选择一个不等于 i 的整数"""j = iwhile j == i:j = int(random.uniform(0, m))return jdef clip_alpha(alpha_j:float, H:float, L:float) -> float:"""修剪 alpha_j"""if alpha_j > H:alpha_j = Hif alpha_j < L:alpha_j = Lreturn alpha_j
简化SMO的代码实现,smoSimple.py:
from smo_assist import (select_Jrandom, clip_alpha)import numpy as np
import pdbdef smoSimple(data_mat_in:np.ndarray, class_labels:np.ndarray, C:float, toler:float, max_iter:int):"""data_mat_in: 数据集class_labels: 类别标签C: 松弛变量toler: 容错率max_iter: 最大迭代次数"""b = 0; # 初始化bm, n = np.shape(data_mat_in) # m: 样本数, n: 特征数alphas = np.zeros((m, 1)) # 初始化alphaiter = 0 # 迭代次数while iter < max_iter:alphaPairsChanged = 0for i in range(m):fXi = float(np.multiply(alphas, class_labels).T @ (data_mat_in @ data_mat_in[i, :].T)) + b"""(1 , m) * (m, n) * (n, 1) = (1, 1) = 标量再 加上 b 就是 f(x) 的值"""Ei = fXi - float(class_labels[i])"""Ei = f(x) - y 预测误差"""if (# 第一种情况:样本被误分类,且权重可以增加((class_labels[i] * Ei < -toler) # 预测误差与标签方向相反,且误差大于容忍度and (alphas[i] < C)) # 当前权重小于正则化参数 C,可以增加权重or # 第二种情况:样本被误分类,且权重需要调整((class_labels[i] * Ei > toler) # 预测误差与标签方向相同,且误差大于容忍度and (alphas[i] > 0)) # 当前权重大于 0,需要调整权重):j = select_Jrandom(i, m)fxj = float(np.multiply(alphas, class_labels).T @ (data_mat_in @ data_mat_in[j, :].T)) + bEj = fxj - float(class_labels[j])alpha_j_old = alphas[j].copy(); alpha_i_old = alphas[i].copy()if (class_labels[i] != class_labels[j]):L = max(0, alphas[j] - alphas[i]) # 左边界H = min(C, C + alphas[j] - alphas[i]) # 右边界else:L = max(0, alphas[j] + alphas[i] - C)H = min(C, alphas[j] + alphas[i])if L == H: continue # 跳出本次循环eta = 2.0 * data_mat_in[i, :] @ data_mat_in[j, :].T - data_mat_in[i, :] @ data_mat_in[i, :].T - data_mat_in[j, :] @ data_mat_in[j, :].T"""计算 eta = K11 + K22 - 2 * K12 = 2 * x_i * x_j - x_i * x_i - x_j * x_j """ if eta >= 0:continuealphas[j] -= class_labels[j] * (Ei - Ej) / eta # 更新权重alphas[j] = clip_alpha(alphas[j], H, L) # 调整权重if abs(alphas[j] - alpha_j_old) < 0.00001:continue # 跳出本次循环,不更新 ialphas[i] += class_labels[j] * class_labels[i] * (alpha_j_old - alphas[j]) # 更新权重b1 = b - Ei - class_labels[i] * (alphas[i] - alpha_i_old) * data_mat_in[i, :] @ data_mat_in[i, :].T - class_labels[j] *(alphas[j] - alpha_j_old) * data_mat_in[i, :] @ data_mat_in[j, :].Tb2 = b - Ej - class_labels[i] * (alphas[i] - alpha_i_old) * data_mat_in[i, :] @ data_mat_in[j, :].T - class_labels[j] *(alphas[j] - alpha_j_old) * data_mat_in[j, :] @ data_mat_in[j, :].T"""更新 b""" if 0 < alphas[i] < C:b = b1elif 0 < alphas[j] < C:b = b2else:b = (b1 + b2) / 2.0alphaPairsChanged += 1if alphaPairsChanged == 0:iter += 1else:iter = 0return b, alphasif __name__ == '__main__':print( smoSimple(np.array([[1, 2], [3, 4]]), np.array([[-1],[1]]), 0.6, 0.001, 40))
test.py:
from data_processing import *
from smoSimple import *
import numpy as np
import matplotlib.pyplot as plt# 数据处理和 SVM 训练
data_mat_in, class_labels = data_processing()
b, alphas = smoSimple(data_mat_in, class_labels, 0.6, 0.001, 40)# 打印结果
print("Bias (b):", b)
print("Non-zero alphas:", alphas[alphas > 0])# 打印数据形状
print("Shape of data_mat_in:", np.shape(data_mat_in))
print("Shape of class_labels:", np.shape(class_labels))# 将 Y 转换为一维数组(如果它是二维的)
Y = class_labels
# 提取不同类别的索引
class_1_indices = np.where(Y == 1)[0] # 类别为 1 的样本索引
class_2_indices = np.where(Y == -1)[0] # 类别为 -1 的样本索引
X = data_mat_in# 绘制散点图
plt.figure(figsize=(8, 6))
plt.scatter(X[class_1_indices, 0], X[class_1_indices, 1], c='blue', label='Class 1', alpha=0.5)
plt.scatter(X[class_2_indices, 0], X[class_2_indices, 1], c='red', label='Class -1', alpha=0.5)# 计算权重向量 w
w = np.dot((alphas * Y).T, X).flatten()
# print(f"w: {w}")
print("Shape of X:", X.shape) # 应该是 (m, n)
print("Shape of Y:", Y.shape) # 应该是 (m, 1)
print("Shape of alphas:", alphas.shape) # 应该是 (m, 1)# 绘制超平面
# 超平面方程:w[0] * x1 + w[1] * x2 + b = 0
# 解出 x2: x2 = -(w[0] * x1 + b) / w[1]
x1 = np.linspace(np.min(X[:, 0]), np.max(X[:, 0]), 100)
x2 = -(w[0] * x1 + b) / w[1]
print(f"w_shape: {w.shape}")
# 绘制超平面
plt.plot(x1, x2, label='SVM Hyperplane', color='green', linewidth=2)# 标出支持向量
support_vectors_indices = np.where(alphas > 0)[0] # 找到所有支持向量的索引
plt.scatter(X[support_vectors_indices, 0], X[support_vectors_indices, 1], facecolors='none', edgecolors='k', s=50, label='Support Vectors')# 添加图例和标签
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Scatter Plot of Data with SVM Hyperplane')
plt.legend()# 显示图形
plt.show()

ML_AI_SourceCode-/支持向量机 at master · sjyttkl/ML_AI_SourceCode- (github.com)
机器学习:支持向量机(SVM)-CSDN博客
【整理】深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件 - mo_wang - 博客园 (cnblogs.com)
机器学习(四):通俗理解支持向量机SVM及代码实践 - 知乎 (zhihu.com)
相关文章:

机器学习:支持向量机
支持向量机(Support Vector Machine)是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的广义线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。 假设两类数据可以被 H x : w T x…...

人工智能前沿技术进展与应用前景探究
一、引言 1.1 研究背景与意义 人工智能作为一门极具变革性的前沿技术,正深刻地改变着人类社会的各个层面。从其诞生之初,人工智能便承载着人类对智能机器的无限遐想与探索。自 20 世纪中叶起,人工智能踏上了它的发展征程,历经了…...

(一)HTTP协议 :请求与响应
前言 爬虫需要基础知识,HTTP协议只是个开始,除此之外还有很多,我们慢慢来记录。 今天的HTTP协议,会有助于我们更好的了解网络。 一、什么是HTTP协议 (1)定义 HTTP(超文本传输协议ÿ…...

什么是网络爬虫?Python爬虫到底怎么学?
最近我在研究 Python 网络爬虫,发现这玩意儿真是有趣,干脆和大家聊聊我的心得吧!咱们都知道,网络上的信息多得就像大海里的水,而网络爬虫就像一个勤劳的小矿工,能帮我们从这片浩瀚的信息海洋中挖掘出需要的…...

NR_shell运行流程简析
nr_shell 是一套开源 shell 框架,基于框架可创建终端交互功能。 为了记录终端输入指令,以及进行解析处理,nr_shell 提供了一套 cmd 结构体,具体如下:typedef struct static_cmd_function_struct {char cmd[NR_SHELL_CM…...
)
CSS Fonts(字体)
CSS Fonts(字体) 在网页设计中,字体是传达信息情感和风格的关键元素。CSS(层叠样式表)提供了丰富的字体样式和属性,使得网页设计者能够根据需求选择合适的字体,从而提升用户体验。本文将详细介绍CSS字体相关的知识,包括字体的选择、加载、样式设置等。 字体的选择 选…...

基于Django的Boss直聘IT岗位可视化分析系统的设计与实现
【Django】基于Django的Boss直聘IT岗位可视化分析系统的设计与实现(完整系统源码开发笔记详细部署教程)✅ 目录 一、项目简介二、项目界面展示三、项目视频展示 一、项目简介 该系统采用Python作为主要开发语言,利用Django这一高效、安全的W…...

linux系统中的 scp的使用方法
SCP(Secure Copy Protocol)是一种通过加密的方式在本地主机和远程主机之间安全地传输文件的协议。 它是基于SSH协议的扩展,允许用户在不同主机之间进行文件复制和传输,是Linux和Unix系统中常用的工具之一。 在嵌入式Linux软件的…...
)
x5music3.0 admin_index.php 后台权限绕过漏洞复现(附脚本)
免责申明: 本文所描述的漏洞及其复现步骤仅供网络安全研究与教育目的使用。任何人不得将本文提供的信息用于非法目的或未经授权的系统测试。作者不对任何由于使用本文信息而导致的直接或间接损害承担责任。如涉及侵权,请及时与我们联系,我们将尽快处理并删除相关内容。 0x0…...

【单链表算法实战】解锁数据结构核心谜题——相交链表
题目如下: 解题过程如下: 相交链表只可以在中间任意位置/头/尾结点相交,如下图: 一个next指针只能指向一块地址,所以不会出现这种情况: 在返回相交链表的起始结点之前先要判断两个链表是否相交࿰…...

Crewai框架添加日志功能
一开始看官方文档以为要用callback这个注释在一个自定义函数上输出日志,结果弄半天都没有结果,最后发已经有现成的方法了(一开始搜log都没搜到这个方法) 只要添加这个output_log_file配置参数即可,由于我的项目只有一…...

【2025年数学建模美赛E题】(农业生态系统)完整解析+模型代码+论文
生态共生与数值模拟:生态系统模型的物种种群动态研究 摘要1Introduction1.1Problem Background1.2Restatement of the Problem1.3Our Work 2 Assumptions and Justifications3 Notations4 模型的建立与求解4.1 农业生态系统模型的建立与求解4.1.1 模型建立4.1.2求解…...

Linux(Centos、Ubuntu) 系统安装jenkins服务
该文章手把手演示在Linux系统下如何安装jenkins服务、并自定义jenkins数据文件位置、以及jenkins如何设置国内镜像源加速,解决插件下载失败问题 安装方式:war包安装 阿里云提供的war下载源地址:https://mirrors.aliyun.com/jenkins/war/?s…...

2013年蓝桥杯第四届CC++大学B组真题及代码
目录 1A:高斯日记(日期计算) 2B:马虎的算式(暴力模拟) 3C:第39级台阶(dfs或dp) 4D:黄金连分数(递推大数运算) 5E:前缀…...

TDengine 做为 FLINK 数据源技术参考手册
Apache Flink 是一款由 Apache 软件基金会支持的开源分布式流批一体化处理框架,可用于流处理、批处理、复杂事件处理、实时数据仓库构建及为机器学习提供实时数据支持等诸多大数据处理场景。与此同时,Flink 拥有丰富的连接器与各类工具,可对接…...

21.2、网络设备安全机制与实现技术
目录 网络设备安全机制与实现技术 - 认证技术网络设备安全机制与实现技术 - 访问控制网络设备安全机制与实现技术 - 信息加密网络设备安全机制与实现技术 - 安全通信网络设备安全机制与实现技术 - 日志审计网络设备安全机制与实现技术 - 安全增强网络设备安全机制与实现技术 - …...

数据结构:二叉树—面试题(二)
1、二叉树的最近公共祖先 习题链接https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/ 描述: 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点…...

OFD、PDF 电子签章系统处理流程
在C#中实现电子签章系统的处理流程,可以参考以下步骤和技术实现: 1. 电子签章系统的基本流程 电子签章系统的核心流程包括以下几个步骤: 密钥生成:生成公钥和私钥对,私钥由签章人保管,公钥用于验证签名。…...

分布式微服务系统简述
distributed microservice 分布式与微服务的定义及关系;分布式微服务架构里的各组件,如:配置中心、服务注册/发现、服务网关、负载均衡器、限流降级、断路器、服务调用、分布式事务等;spring cloud 介绍及实现案例,如…...

【Linux】列出所有连接的 WiFi 网络的密码
【Linux】列出所有连接的 WiFi 网络的密码 终端输入 sudo grep psk /etc/NetworkManager/system-connections/*会列出所有连接过 Wifi 的信息,格式类似 /etc/NetworkManager/system-connections/AAAAA.nmconnection:pskBBBBBAAAAA 是 SSID,BBBBB 是对…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
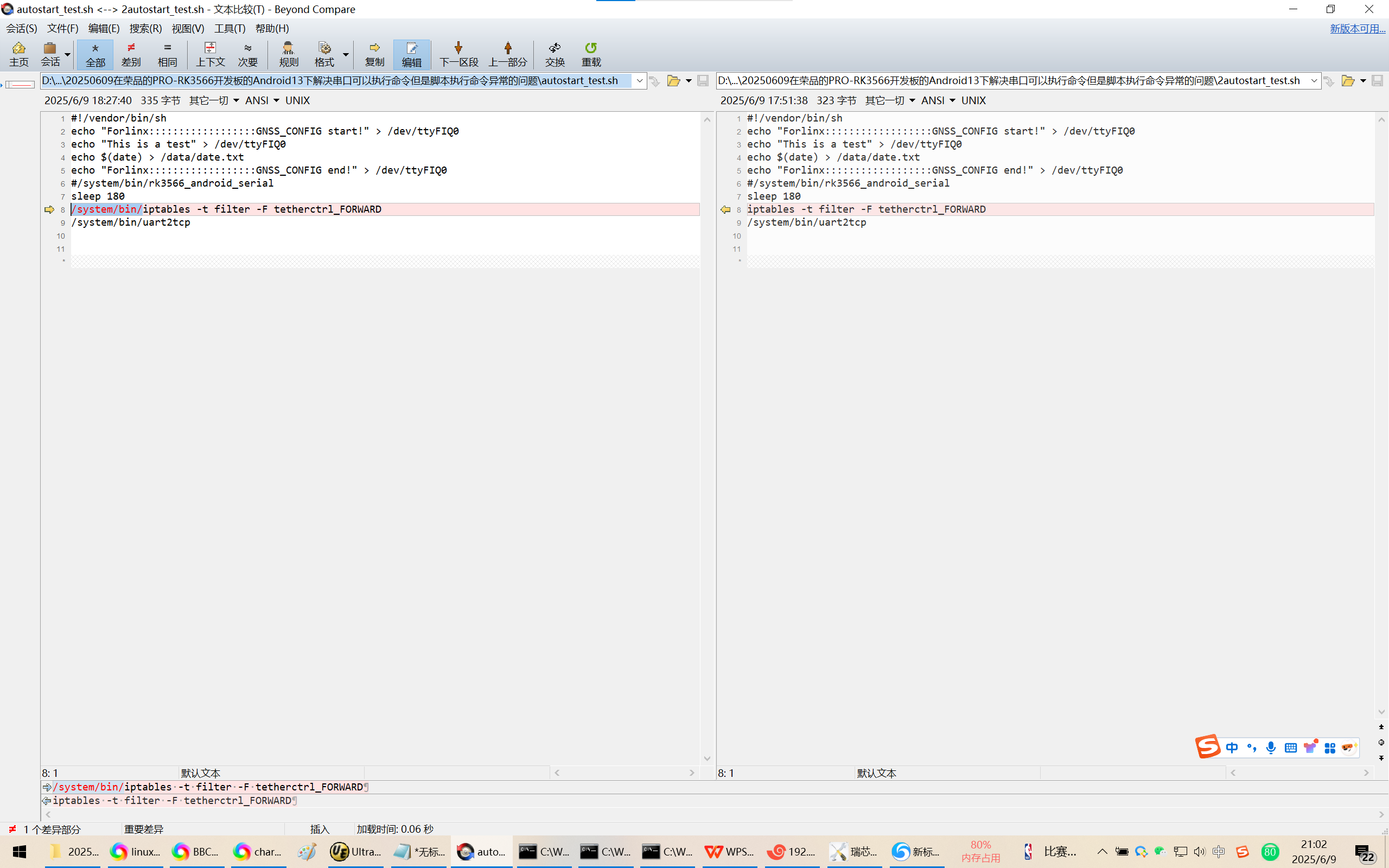
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...
