【二分查找】力扣373. 查找和最小的 K 对数字
给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。
示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数:
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
示例 2:
输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数:
[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

二分
class Solution {
public:vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {int m = nums1.size();int n = nums2.size();auto count = [&](int target){int start = 0;int end = n - 1;long long cnt = 0;while(start < m && end >= 0){if(nums1[start] + nums2[end] > target){end--;}else{cnt += end + 1;start++;}}return cnt;};int left = nums1[0] + nums2[0];int right = nums1[m-1] + nums2[n-1];while(left < right){int mid = (left + right) >> 1;if(count(mid) < k){left = mid + 1;}else{right = mid;}}vector<vector<int>> ans;int pos = n - 1;for(int i = 0; i < m; i++){while(pos >= 0 && nums1[i] + nums2[pos] >= left){pos--;}for(int j = 0; j <= pos && k > 0; k--, j++){ans.push_back({nums1[i], nums2[j]});}}pos = n - 1;for(int i = 0; i < m && k > 0; i++){int start1 = i;while(i < m - 1 && nums1[i] == nums1[i+1]){i++;}while(pos >= 0 && nums1[i] + nums2[pos] > left){pos--;}int start2 = pos;while(pos > 0 && nums2[pos] == nums2[pos-1]){pos--;}if(nums1[i] + nums2[pos] != left){continue;}int count = min((long)k, (long)(i - start1 + 1) * (start2 - pos + 1));for(int j = 0; j < count && k > 0; j++, k--){ans.push_back({nums1[i], nums2[pos]});}}return ans;}
};
使用二分法实际上就是另外一种使用试探的方式。nums1[0] + nums2[0]是两个数组元素和的最小值,组成二分下界,nums1[m-1] + nums2[n-1]组成二分上界。我们使用二分查找,查找出当和为多少的时候,刚好是第k对数字。
我们定义一个count函数,count函数的目的实际上就是计算出小于等于我们传入的mid的组合一共有多少个,以便与k进行比较,从而找出我们最终需要的和是多少。
最终二分查找结束,left便是和第k小的元素对的和。由于我们最终要返回的是前k小的所有的数组对。那么我们在代码中首先先要找出和比left小的数组对是什么。
vector<vector<int>> ans;int pos = n - 1;for(int i = 0; i < m; i++){while(pos >= 0 && nums1[i] + nums2[pos] >= left){pos--;}for(int j = 0; j <= pos && k > 0; k--, j++){ans.push_back({nums1[i], nums2[j]});}}
接下来我们要查找出和等于left的元素对
pos = n - 1;for(int i = 0; i < m && k > 0; i++){int start1 = i;while(i < m - 1 && nums1[i] == nums1[i+1]){i++;}while(pos >= 0 && nums1[i] + nums2[pos] > left){pos--;}int start2 = pos;while(pos > 0 && nums2[pos] == nums2[pos-1]){pos--;}if(nums1[i] + nums2[pos] != left){continue;}int count = min((long)k, (long)(i - start1 + 1) * (start2 - pos + 1));for(int j = 0; j < count && k > 0; j++, k--){ans.push_back({nums1[i], nums2[pos]});}}
最后返回ans即是答案
相关文章:

【二分查找】力扣373. 查找和最小的 K 对数字
给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。 定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。 请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。 示例 1: 输入: nums1 [1,7,11], nums2 …...

池化层Pooling Layer
1. 定义 池化是对特征图进行的一种压缩操作,通过在一个小的局部区域内进行汇总统计,用一个值来代表这个区域的特征信息,常用于卷积神经网络(CNN)中。 2. 作用 提取代表性信息的同时降低特征维度,具有平移…...

力扣算法题——11.盛最多水的容器
目录 💕1.题目 💕2.解析思路 本题思路总览 借助双指针探索规律 从规律到代码实现的转化 双指针的具体实现 代码整体流程 💕3.代码实现 💕4.完结 二十七步也能走完逆流河吗 💕1.题目 💕2.解析思路…...

自由学习记录(32)
文件里找到切换颜色空间 fgui中的 颜色空间是一种总体使用前的设定 颜色空间,和半透明混合产生的效果有差异,这种问题一般可以产生联系 动效就是在fgui里可以编辑好,然后在unity中也准备了对应的调用手段,可以详细的使用每一个具…...
)
VScode+Latex (Recipe terminated with fatal error: spawn xelatex ENOENT)
使用VSCode编辑出现Recipe terminated with fatal error: spawn xelatex ENOENT问题咋办? 很好解决,大概率的原因是因为latex没有添加到系统环境变量中,所有设置的编译工具没有办法找到才出现的这种情况。 解决方法: winR 然后输…...
)
「蓝桥杯题解」蜗牛(Java)
题目链接 这道题我感觉状态定义不太好想,需要一定的经验 import java.util.*; /*** 蜗牛* 状态定义:* dp[i][0]:到达(x[i],0)最小时间* dp[i][1]:到达 xi 上方的传送门最小时间*/public class Main {static Scanner in new Scanner(System.in);static f…...
 详解)
PHP EOF (Heredoc) 详解
PHP EOF (Heredoc) 详解 PHP 中的 EOF(End Of File)是一种非常有用的语法特性,允许开发者创建多行字符串。它特别适合于创建格式化文本,如配置文件、HTML 模板等。本文将详细讲解 PHP EOF 的用法、优势以及注意事项。 什么是 EOF? EOF 是一种特殊的字符串定义方式,它允…...

pyautogui操控Acrobat DC pro万能PDF转Word,不丢任何PDF格式样式
为了将PDF转换脚本改为多进程异步处理,我们需要确保每个进程独立操作不同的Acrobat窗口。以下是实现步骤: 实现代码 import os import pyautogui import time import subprocess import pygetwindow as gw from multiprocessing import Pooldef conver…...

Day32:字符串的复制
在 Python 中,字符串的复制是指创建一个新的字符串,它的内容与原字符串相同。字符串是不可变的对象,这意味着你不能直接修改字符串的内容,但是可以通过复制来创建新的字符串进行操作。字符串的复制在一些情况下非常有用࿰…...

基于Mybatis继承AbstractRoutingDataSource使用自定义注解实现动态数据源
一:实现 方式一:继承AbstractRoutingDataSource使用自定义注解实现 环境:springboot3 MyBatis3 mysql-connector8 DataSourceKeyEnum枚举类 有几个数据源就配置几个枚举类,和数据源数量一一对应 class DataSourceKeyEnum{D…...

ZooKeeper 数据模型
ZooKeeper 数据模型 ZooKeeper 拥有层次化的命名空间,类似分布式文件系统,但每个节点不仅能有子节点,还可关联数据。节点路径为规范的绝对路径,用斜杠分隔,无相对引用。路径命名有如下约束: 路径名不能包…...

【VUE】Vue2中Vue.extend方法
在 Vue.js 2.x 版本中,Vue.extend() 方法被用于创建一个新的 Vue 子类,可以在该子类上扩展一些属性、指令和组件选项等,然后进行实例化。 比如,可以在创建一些类似 loading 式的函数式插件时,使用: 在 Vue…...

MaskGAE论文阅读
What’s Behind the Mask: Understanding Masked Graph Modeling for Graph Autoencoders 碎碎念:一篇论文看四天,效率也没谁了(捂脸) 看一点忘一点,虽然在本子上有记录,但还是忘,下次看一点在博客上记一点启发 本来很…...

Mybatis-plus 更新 Null 的策略踩坑记
一个bug 在一个管理页面,有一个非必填字段被设置成空了并提交更新,再次打开的时候,发现字段还在,并没有被更新成功。 使用的数据库映射框架是 Mybatis-plus ,对于Mybatis 在更新字段的时候会对空进行校验,…...

Oracle迁移DM数据库
Oracle迁移DM数据库 本文记录使用达梦官方数据迁移工具DTS,将Oracle数据库的数据迁移至达梦数据库。 1 数据准备 2 DTS工具操作步骤 2.1 创建工程 打开DTS迁移工具,点击新建工程,填写好工程信息,如图: 2.2 新建迁…...

HTML特殊符号的使用示例
目录 一、基本特殊符号的使用 1、空格符号: 2、小于号 和 大于号: 3、引号: 二、版权、注册商标符号的使用 1、版权符号:© 2、注册商标符号: 三、数学符号的使用 四、箭头符号的使用 五、货币符号的使用…...
—排序算法小结》)
数据结构基础之《(15)—排序算法小结》
一、排序算法的稳定性 1、稳定性是指同样大小的样本再排序之后不会改变相对次序 2、对基础类型来说,稳定性毫无意义 比如:3和3没有区别。《潜伏》里说同样两个一百元大钞,你能告诉我哪一个是高尚的那一个是龌龊的么 3、对非基础类型来说&a…...

Linux系统下速通stm32的clion开发环境配置
陆陆续续搞这个已经很久了。 因为自己新电脑是linux系统无法使用keil,一开始想使用vscode里的eide但感觉不太好用;后面想直接使用cudeide但又不想妥协,想趁着这个机会把linux上的其他单片机开发配置也搞明白;而且非常想搞懂cmake…...

【2024年 CSDN博客之星】我的2024年创作之旅:从C语言到人工智能,个人成长与突破的全景回顾
我的2024年创作之旅:从C语言到人工智能,个人成长与突破的全景回顾 引言 回望2024年,我不仅收获了技术上的成长,更收获了来自CSDN平台上无数粉丝、朋友以及网友们的支持与鼓励。在这条创作之路上,CSDN不仅是我展示技术成…...
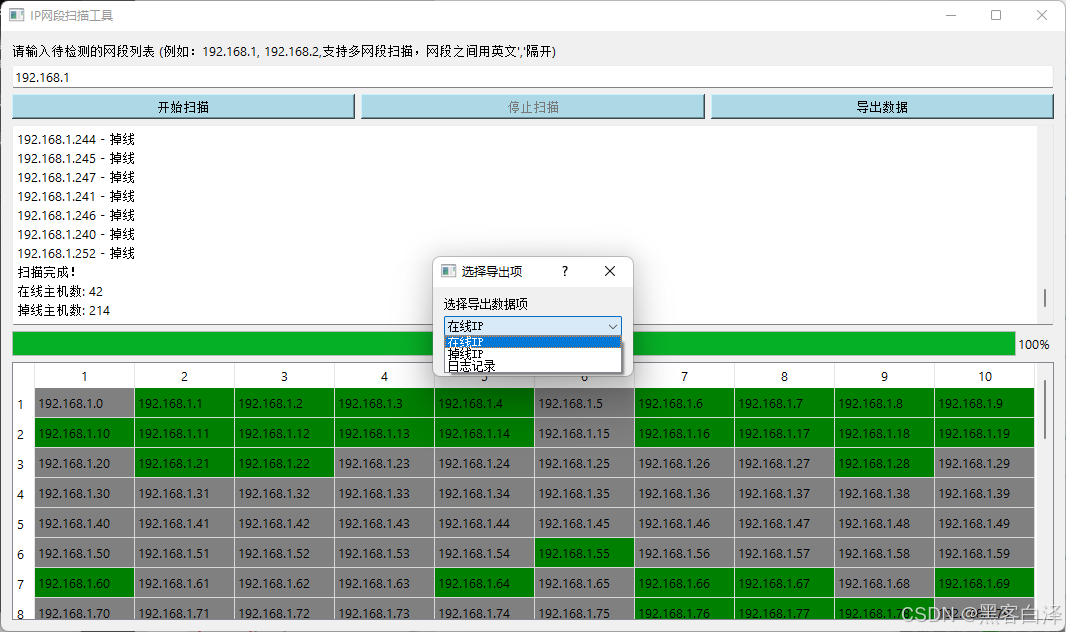
Python 轻松扫描,快速检测:高效IP网段扫描工具全解析
Python 轻松扫描,快速检测:高效IP网段扫描工具全解析 相关资源文件已经打包成EXE文件,可双击直接运行程序,且文章末尾已附上相关源码,以供大家学习交流,博主主页还有更多Python相关程序案例,秉着…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
