吴恩达深度学习——如何实现神经网络
来自吴恩达深度学习,仅为本人学习所用。
文章目录
- 神经网络的表示
- 计算神经网络的输出
- 激活函数
- tanh
- 选择激活函数
- 为什么需要非激活函数
- 双层神经网络的梯度下降法
- 随机初始化
神经网络的表示
对于简单的Logistic回归,使用如下的计算图。

如果是多个神经元组合起来构成一个神经网络,计算图如下
输入特征 x 1 , x 2 , x 3 x1, x2, x3 x1,x2,x3所在的层是输入层;中间的三个圆圈所在的层是隐藏层,在训练集中找不到隐藏层的数据;最后的一个圆圈所在的层是输出层,直接输出 y ^ \hat{y} y^。
使用上标 [ 1 ] [1] [1]、 [ 2 ] [2] [2]表示第一层,第二层的神经网络。之前使用 X \mathbf{X} X表示输入的特征值,也可以使用 a [ 0 ] \mathbf{a}^{[0]} a[0]表示网络中的输入层;中间的隐藏层使用 a [ 1 ] \mathbf{a}^{[1]} a[1]表示,从上往下的圆圈分别为 a 1 [ 1 ] 、 a 2 [ 1 ] 、 a 3 [ 1 ] 、 a 4 [ 1 ] a^{[1]}_1、a^{[1]}_2、a^{[1]}_3、a^{[1]}_4 a1[1]、a2[1]、a3[1]、a4[1],有 a [ 1 ] = [ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] a 4 [ 1 ] ] \mathbf{a}^{[1]}=\begin{bmatrix} a^{[1]}_1\\ a^{[1]}_2\\ a^{[1]}_3\\ a^{[1]}_4 \end{bmatrix} a[1]= a1[1]a2[1]a3[1]a4[1] ;最后产生 a [ 2 ] \mathbf{a}^{[2]} a[2]。
该神经网络是个2层的神经网络(隐藏层+输出层),一般不把输入层看作一个标准的层。隐藏层及最后的输出层是带有参数的。

在上面的计算图中,先计算第一层的Logistic回归,然后将计算出的 a [ 1 ] a^{[1]} a[1]作为下一层的 X X X继续计算第二层的Logistic回归,最后计算到损失函数,完成一次正向传播;接着求导完成反向传播。
计算神经网络的输出

分别计算 a 1 [ 1 ] a^{[1]}_1 a1[1]和 a 2 [ 1 ] a^{[1]}_2 a2[1]

隐藏层的每一个神经元的公式为
有 Z [ 1 ] = [ z 1 [ 1 ] z 2 [ 1 ] z 3 [ 1 ] z 4 [ 1 ] ] = [ — w 1 [ 1 ] T — — w 2 [ 1 ] T — — w 3 [ 1 ] T — — w 4 [ 1 ] T — ] [ x 1 x 2 x 3 ] + [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ] = W [ 1 ] X + b [ 1 ] \mathbf{Z}^{[1]}=\begin{bmatrix} z^{[1]}_1\\ z^{[1]}_2\\ z^{[1]}_3\\ z^{[1]}_4\end{bmatrix}=\begin{bmatrix} —w^{[1]T}_1—\\ —w^{[1]T}_2—\\ —w^{[1]T}_3—\\ —w^{[1]T}_4—\end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\end{bmatrix}+\begin{bmatrix} b^{[1]}_1\\ b^{[1]}_2\\ b^{[1]}_3\\ b^{[1]}_4\end{bmatrix}=\mathbf{W}^{[1]}\mathbf{X}+\mathbf{b}^{[1]} Z[1]= z1[1]z2[1]z3[1]z4[1] = —w1[1]T——w2[1]T——w3[1]T——w4[1]T— x1x2x3 + b1[1]b2[1]b3[1]b4[1] =W[1]X+b[1] a [ 1 ] = [ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] a 4 [ 1 ] ] = σ ( Z [ 1 ] ) \mathbf{a}^{[1]}=\begin{bmatrix} a^{[1]}_1\\ a^{[1]}_2\\ a^{[1]}_3\\ a^{[1]}_4 \end{bmatrix}=\sigma(\mathbf{Z}^{[1]}) a[1]= a1[1]a2[1]a3[1]a4[1] =σ(Z[1])下一层表示为 Z [ 2 ] = W [ 2 ] X + b [ 2 ] \mathbf{Z}^{[2]}=\mathbf{W}^{[2]}\mathbf{X}+\mathbf{b}^{[2]} Z[2]=W[2]X+b[2] a [ 2 ] = [ a 1 [ 2 ] a 2 [ 2 ] a 3 [ 2 ] a 4 [ 2 ] ] = σ ( Z [ 2 ] ) \mathbf{a}^{[2]}=\begin{bmatrix} a^{[2]}_1\\ a^{[2]}_2\\ a^{[2]}_3\\ a^{[2]}_4 \end{bmatrix}=\sigma(\mathbf{Z}^{[2]}) a[2]= a1[2]a2[2]a3[2]a4[2] =σ(Z[2])
激活函数
tanh
tanh 函数,即双曲正切函数,其数学表达式为: tanh ( x ) = e x − e − x e x + e − x \tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} tanh(x)=ex+e−xex−e−x
- 值域: t a n h ( x ) tanh(x) tanh(x) 的值域是 ( − 1 , 1 ) (-1, 1) (−1,1)。当 (x) 趋于正无穷大时, t a n h ( x ) tanh(x) tanh(x)趋近于 1 1 1;当 x x x 趋于负无穷大时, t a n h ( x ) tanh(x) tanh(x) 趋近于 − 1 -1 −1;当 x = 0 x = 0 x=0 时, t a n h ( x ) = 0 tanh(x)=0 tanh(x)=0。
- 形状:它是一个 S 型函数,形状类似于
sigmoid函数,但它的输出范围是(-1, 1),而不是sigmoid函数的(0, 1)。 - 导数: t a n h tanh tanh 函数的导数可以根据其函数形式计算得到, t a n h ′ ( x ) = 1 − tanh 2 ( x ) tanh'(x)=1-\tanh^{2}(x) tanh′(x)=1−tanh2(x),这个性质在反向传播算法中计算梯度时非常有用,因为导数的计算相对简单,并且在x = 0时导数最大,为 1 1 1,随着 x x x 趋于正负无穷,导数趋近于 0 0 0。
好处如下:
- 解决梯度消失问题:相比
sigmoid函数, t a n h tanh tanh函数在一定程度上可以缓解梯度消失问题。因为sigmoid函数在输入绝对值较大时,梯度趋近于 0,导致梯度更新非常缓慢,而 t a n h tanh tanh函数的输出范围更广,其梯度在远离 0 0 0的位置相对sigmoid函数来说更不容易趋近于 0 0 0,在某些情况下可以帮助神经网络更快地收敛。 - 中心化输出: t a n h tanh tanh函数的输出是零均值的,即输出的平均值接近0,这有助于下一层的学习,因为下一层的输入的平均值不会总是正数,避免了
sigmoid函数输出总是正的问题,这可以加快网络的收敛速度。
选择激活函数
到目前为止,如果输出的是0,1之类的二元分类问题,激活函数可以选择sigmoid函数做输出层的激活函数、其他所有单元使用ReLU函数;如果不知道隐藏层使用哪个激活函数,ReLU函数一般默认做隐藏层的激活函数; t a n h tanh tanh函数相对于sigmoid函数更好。
为什么需要非激活函数
如果只是使用线性激活函数,不论一个神经网络有多少层,合并化简后的表达式与单层神经网络的激活函数表达式相同,导致隐藏层没什么作用。

双层神经网络的梯度下降法
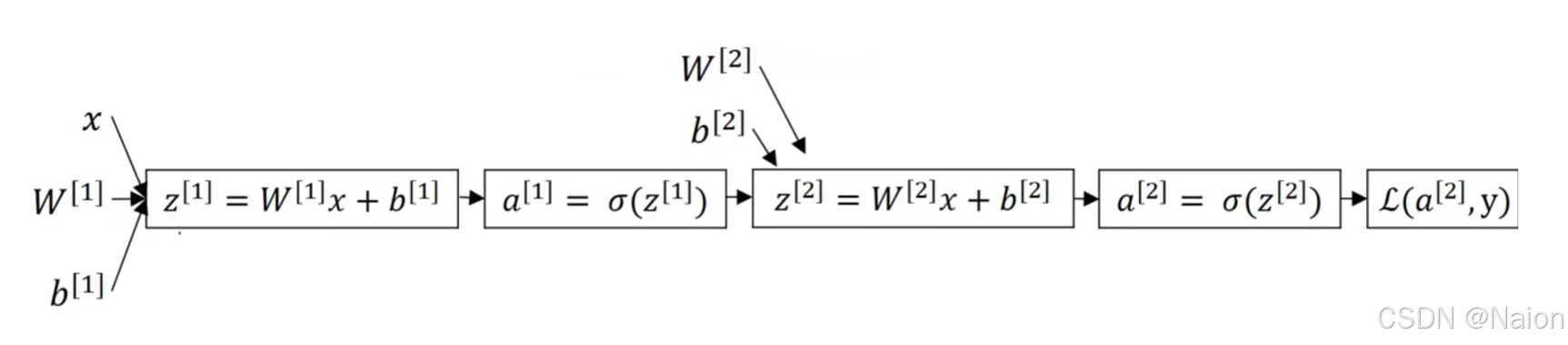
给出上述笔记的双神经网络计算图,反向传播进行计算,有 d a [ 2 ] = d L d a [ 2 ] = − y a [ 2 ] + 1 − y 1 + a [ 2 ] \mathrm{d}a^{[2]}=\frac{\mathrm{d}L}{\mathrm{d}a^{[2]}}=-\frac{y}{a^{[2]}}+\frac{1-y}{1+a^{[2]}} da[2]=da[2]dL=−a[2]y+1+a[2]1−y d a [ 2 ] d z [ 2 ] = e − x ( 1 + e − x ) 2 = a [ 2 ] ( 1 − a [ 2 ] ) \frac{\mathrm{d}a^{[2]}}{\mathrm{d}z^{[2]}}=\frac{e^{-x}}{(1+e^{-x})^2}=a^{[2]}(1-a^{[2]}) dz[2]da[2]=(1+e−x)2e−x=a[2](1−a[2]) d z [ 2 ] = d L d z [ 2 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] = a [ 2 ] − y dz^{[2]}=\frac{\mathrm{d}L}{\mathrm{d}z^{[2]}}=\frac{\mathrm{d}L}{\mathrm{d}a^{[2]}}\frac{\mathrm{d}a^{[2]}}{\mathrm{d}z^{[2]}}=a^{[2]}-y dz[2]=dz[2]dL=da[2]dLdz[2]da[2]=a[2]−y d w [ 2 ] = d L d w [ 2 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d w [ 2 ] = ( a [ 2 ] − y ) ( w [ 2 ] x + b [ 2 ] ) ′ = ( a [ 2 ] − y ) x T = ( a [ 2 ] − y ) ( a [ 1 ] ) T \mathrm{d}w^{[2]}=\frac{\mathrm{d}L}{\mathrm{d}w^{[2]}}=\frac{\mathrm{d}L}{\mathrm{d}a^{[2]}}\frac{\mathrm{d}a^{[2]}}{\mathrm{d}z^{[2]}}\frac{\mathrm{d}z^{[2]}}{\mathrm{d}w^{[2]}} =(a^{[2]}-y)(w^{[2]}x+b^{[2]})'=(a^{[2]}-y)x^T=(a^{[2]}-y)(a^{[1]})^T dw[2]=dw[2]dL=da[2]dLdz[2]da[2]dw[2]dz[2]=(a[2]−y)(w[2]x+b[2])′=(a[2]−y)xT=(a[2]−y)(a[1])T
- 从计算图中可以看出, x x x实际上来自上一层的 a [ 1 ] a^{[1]} a[1]。
- x x x转置是为了满足矩阵运算的维度一致性以及遵循矩阵求导的规则。还记着前面说过,该计算图中, w [ 2 ] w^{[2]} w[2]和 b [ 2 ] b^{[2]} b[2]实际上是一个矩阵,对矩阵求导的时候要满足维度的一致。在单个神经元的场景下, w w w和 b b b实际上是标量,不存在维度一致性的问题。
d b [ 2 ] = d z [ 2 ] \mathrm{d}b^{[2]}=\mathrm{d}z^{[2]} db[2]=dz[2] d a [ 1 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d a [ 1 ] = ( a [ 2 ] − y ) ( w [ 2 ] ) T σ ′ ( z [ 1 ] ) = ( a [ 2 ] − y ) ( w [ 2 ] ) T \mathrm{d}a^{[1]}=\frac{\mathrm{d}L}{\mathrm{d}a^{[2]}}\frac{\mathrm{d}a^{[2]}}{\mathrm{d}z^{[2]}}\frac{\mathrm{d}z^{[2]}}{\mathrm{d}a^{[1]}}=(a^{[2]}-y)(w^{[2]})^{T}\sigma'(z^{[1]})=(a^{[2]}-y)(w^{[2]})^{T} da[1]=da[2]dLdz[2]da[2]da[1]dz[2]=(a[2]−y)(w[2])Tσ′(z[1])=(a[2]−y)(w[2])T
d z [ 1 ] = d L d a [ 1 ] d a [ 1 ] d z [ 1 ] = ( a [ 2 ] − y ) ( w [ 2 ] ) T ⊙ σ ′ ( z [ 1 ] ) \mathrm{d}z^{[1]}=\frac{\mathrm{d}L}{\mathrm{d}a^{[1]}}\frac{\mathrm{d}a^{[1]}}{\mathrm{d}z^{[1]}}=(a^{[2]}-y)(w^{[2]})^{T}\odot\sigma'(z^{[1]}) dz[1]=da[1]dLdz[1]da[1]=(a[2]−y)(w[2])T⊙σ′(z[1])
⊙ \odot ⊙:对于两个维度相同的向量 x = ( x 1 , x 2 , ⋯ , x n ) \mathbf{x}=(x_1,x_2,\cdots,x_n) x=(x1,x2,⋯,xn) 和 y = ( y 1 , y 2 , ⋯ , y n ) \mathbf{y}=(y_1,y_2,\cdots,y_n) y=(y1,y2,⋯,yn) ,它们的逐元素乘积 z = x ⊙ y = ( x 1 y 1 , x 2 y 2 , ⋯ , x n y n ) \mathbf{z}=\mathbf{x}\odot\mathbf{y}=(x_1y_1,x_2y_2,\cdots,x_ny_n) z=x⊙y=(x1y1,x2y2,⋯,xnyn) 。
随机初始化
对称性问题是指如果神经网络中多个神经元的权重初始值相同,就会出现对称性问题。例如,在一个多层神经网络中,若同一层的神经元初始权重都一样,那么在正向传播时,它们对输入的处理完全相同,反向传播时梯度更新也相同,这使得神经元无法学习到不同的特征,网络的表达能力受限。为避免这种情况,通常采用随机初始化权重的方法。
对于Logistic函数,将权重初始化为0是可以的,但是如果将神经网络的各参数全部初始化为0,导致隐藏单元一直在做同样的计算,对输出单元的影响一样大,多次迭代后两个隐藏单元一直在做重复的计算,也就是对称性问题。这个时候,多个隐藏单元是没有意义的,在使用梯度下降将会无效。
对于该问题,解决方案的随机初始化所有的参数。
w = np.random.randn((2,2)) * 0.01
相关文章:

吴恩达深度学习——如何实现神经网络
来自吴恩达深度学习,仅为本人学习所用。 文章目录 神经网络的表示计算神经网络的输出激活函数tanh选择激活函数为什么需要非激活函数双层神经网络的梯度下降法 随机初始化 神经网络的表示 对于简单的Logistic回归,使用如下的计算图。 如果是多个神经元…...

《STL基础之vector、list、deque》
【vector、list、deque导读】vector、list、deque这三种序列式的容器,算是比较的基础容器,也是大家在日常开发中常用到的容器,因为底层用到的数据结构比较简单,笔者就将他们三者放到一起做下对比分析,介绍下基本用法&a…...

LockSupport概述、阻塞方法park、唤醒方法unpark(thread)、解决的痛点、带来的面试题
目录 ①. 什么是LockSupport? ②. 阻塞方法 ③. 唤醒方法(注意这个permit最多只能为1) ④. LockSupport它的解决的痛点 ⑤. LockSupport 面试题目 ①. 什么是LockSupport? ①. 通过park()和unpark(thread)方法来实现阻塞和唤醒线程的操作 ②. LockSupport是一个线程阻塞…...
Android开发基础知识
1 什么是Android? Android(读音:英:[ndrɔɪd],美:[ˈnˌdrɔɪd]),常见的非官方中文名称为安卓,是一个基于Linux内核的开放源代码移动操作系统,由Google成立…...

C++ Lambda 表达式的本质及原理分析
目录 1.引言 2.Lambda 的本质 3.Lambda 的捕获机制的本质 4.捕获方式的实现与底层原理 5.默认捕获的实现原理 6.捕获 this 的机制 7.捕获的限制与注意事项 8.总结 1.引言 C 中的 Lambda 表达式是一种匿名函数,最早在 C11 引入,用于简化函数对象的…...
《多线程基础之条件变量》
【条件变量导读】条件变量是多线程中比较灵活而且容易出错的线程同步手段,比如:虚假唤醒、为啥条件变量要和互斥锁结合使用?windows和linux双平台下,初始化、等待条件变量的api一样吗? 本文将分别为您介绍条件变量在w…...
21款炫酷烟花合集
系列专栏 《Python趣味编程》《C/C趣味编程》《HTML趣味编程》《Java趣味编程》 写在前面 Python、C/C、HTML、Java等4种语言实现18款炫酷烟花的代码。 Python Python烟花① 完整代码:Python动漫烟花(完整代码) Python烟花② 完整…...

智能风控 数据分析 groupby、apply、reset_index组合拳
目录 groupby——分组 本例 apply——对每个分组应用一个函数 等价用法 reset_index——重置索引 使用前编辑 注意事项 groupby必须配合聚合函数、 关于agglist 一些groupby试验 1. groupby对象之后。sum(一个列名) 2. groupby对象…...

Python网络自动化运维---用户交互模块
文章目录 目录 文章目录 前言 实验环境准备 一.input函数 代码分段解析 二.getpass模块 前言 在前面的SSH模块章节中,我们都是将提供SSH服务的设备的账户/密码直接写入到python代码中,这样很容易导致账户/密码泄露,而使用Python中的用户交…...

【JVM】调优
目的: 减少minor gc、full gc的次数,也就是减少STW的时间,因为java虚拟机在做后台垃圾收集线程的时候,会停掉其他线程,专门做垃圾收集,这样会影响网站的性能,以及用户的体验。 调优位置&#x…...
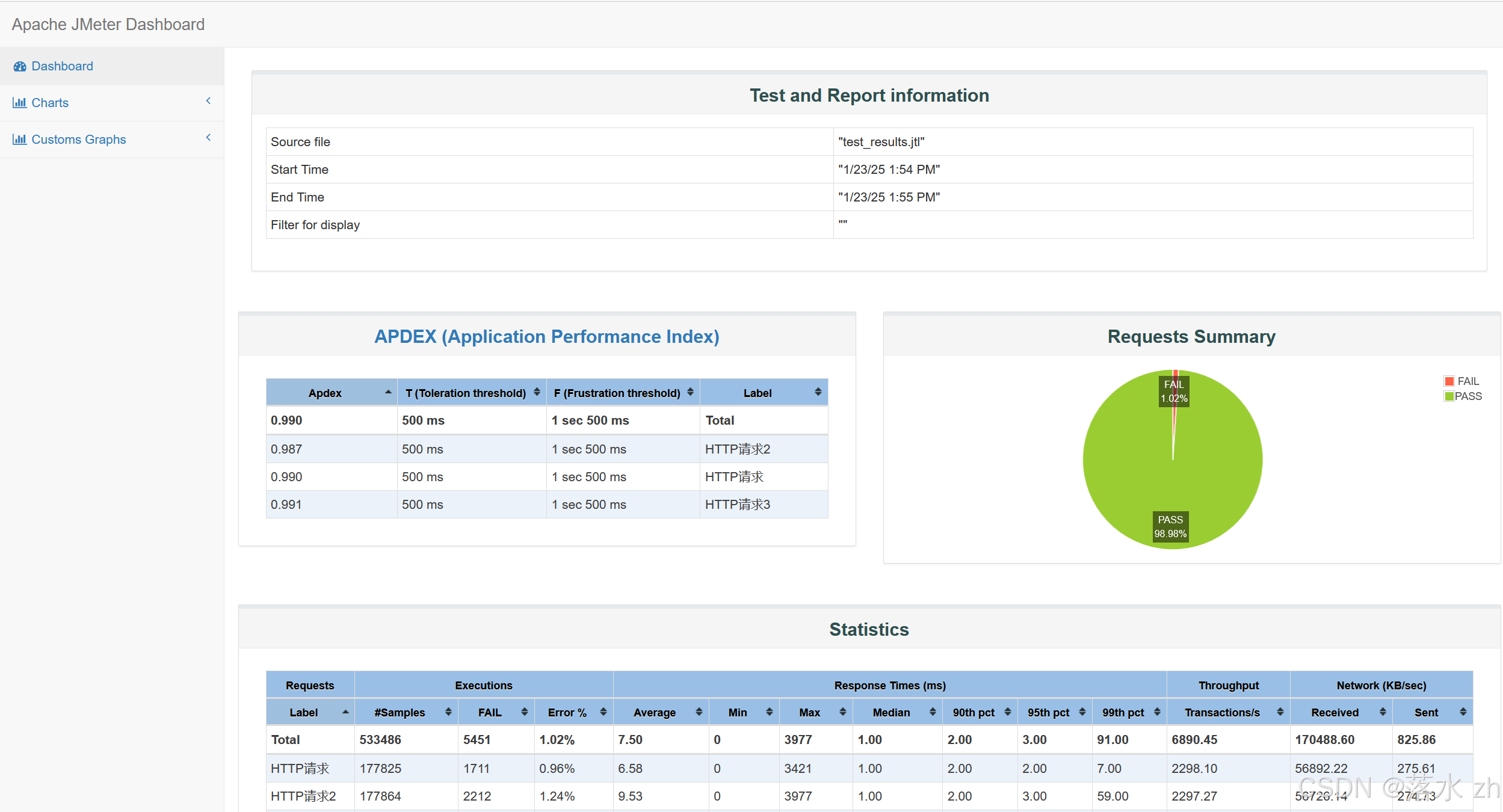
软件测试 —— jmeter(2)
软件测试 —— jmeter(2) HTTP默认请求头(元件)元件作用域和取样器作用域HTTP Cookie管理器同步定时器jmeter插件梯度压测线程组(Stepping Thread Group)参数解析总结 Response Times over TimeActive Thre…...
为什么LabVIEW适合软硬件结合的项目?
LabVIEW是一种基于图形化编程的开发平台,广泛应用于软硬件结合的项目中。其强大的硬件接口支持、实时数据采集能力、并行处理能力和直观的用户界面,使得它成为工业控制、仪器仪表、自动化测试等领域中软硬件系统集成的理想选择。LabVIEW的设计哲学强调模…...

【机器学习】自定义数据集 使用tensorflow框架实现逻辑回归并保存模型,然后保存模型后再加载模型进行预测
一、使用tensorflow框架实现逻辑回归 1. 数据部分: 首先自定义了一个简单的数据集,特征 X 是 100 个随机样本,每个样本一个特征,目标值 y 基于线性关系并添加了噪声。tensorflow框架不需要numpy 数组转换为相应的张量࿰…...

.NET Core缓存
目录 缓存的概念 客户端响应缓存 cache-control 服务器端响应缓存 内存缓存(In-memory cache) 用法 GetOrCreateAsync 缓存过期时间策略 缓存的过期时间 解决方法: 两种过期时间策略: 绝对过期时间 滑动过期时间 两…...
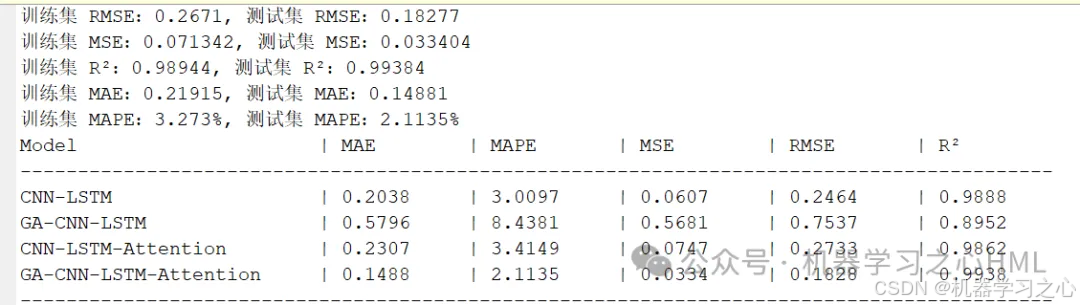
GA-CNN-LSTM-Attention、CNN-LSTM-Attention、GA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比
GA-CNN-LSTM-Attention、CNN-LSTM-Attention、GA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比 目录 GA-CNN-LSTM-Attention、CNN-LSTM-Attention、GA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比预测效果基本介绍程序设计参考资料 预测效果 基本介绍 基于GA-CNN-LST…...
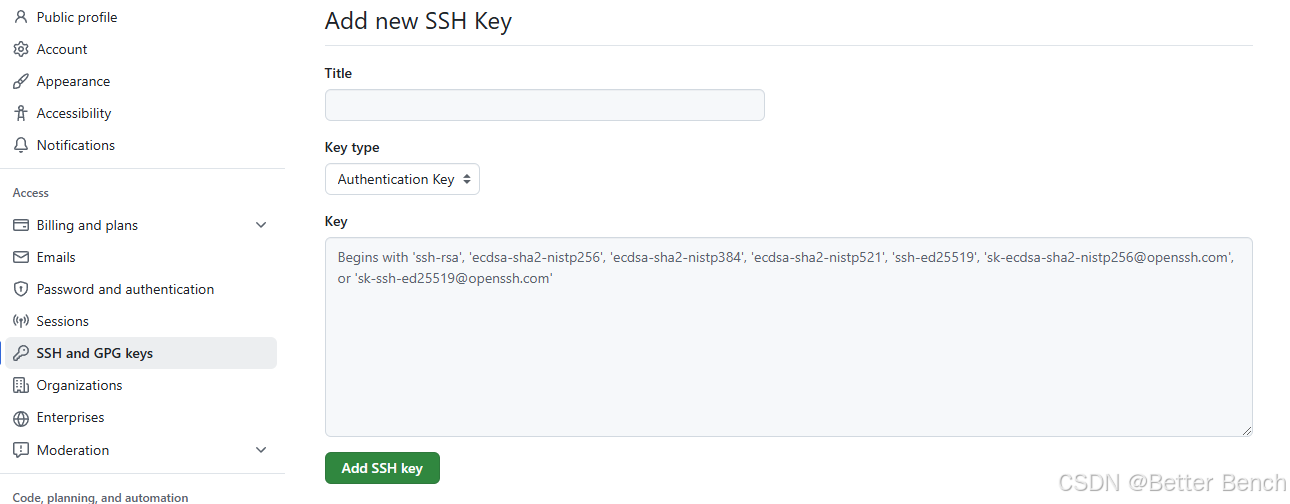
git Bash通过SSH key 登录github的详细步骤
1 问题 通过在windows 终端中的通过git登录github 不再是通过密码登录了,需要本地生成一个密钥,配置到gihub中才能使用 2 步骤 (1)首先配置用户名和邮箱 git config --global user.name "用户名"git config --global…...
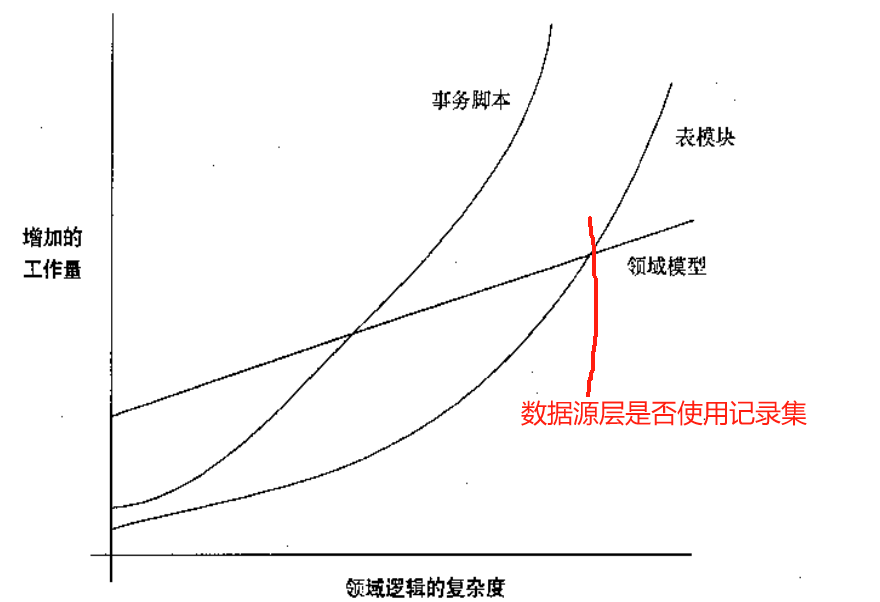
《企业应用架构模式》笔记
领域逻辑 表模块和数据集一起工作-> 先查询出一个记录集,再根据数据集生成一个(如合同)对象,然后调用合同对象的方法。 这看起来很想service查询出一个对象,但调用的是对象的方法,这看起来像是充血模型…...
 (void *)) _IO_funlockfile)
深入理解 C 语言函数指针的高级用法:(void (*) (void *)) _IO_funlockfile
深入理解 C 语言函数指针的高级用法 函数指针是 C 语言中极具威力的特性,广泛用于实现回调、动态函数调用以及灵活的程序设计。然而,复杂的函数指针声明常常让即使是有经验的开发者也感到困惑。本文将从函数指针的基本概念出发,逐步解析复杂…...

【JavaSE】图书管理系统
前言:为了巩固之前学习的java知识点,我们用之前学习的java知识点(方法,数组,类和对象,封装,继承,多态,抽象类,接口)来实现一个简单的图书管理系统…...

【C++数论】880. 索引处的解码字符串|2010
本文涉及知识点 数论:质数、最大公约数、菲蜀定理 LeetCode880. 索引处的解码字符串 给定一个编码字符串 s 。请你找出 解码字符串 并将其写入磁带。解码时,从编码字符串中 每次读取一个字符 ,并采取以下步骤: 如果所读的字符是…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
