【hot100】刷题记录(6)-轮转数组
题目描述:
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
我的作答:
切片,再替换
class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not return anything, modify nums in-place instead."""if not nums: return []if k>len(nums):k = k%len(nums) #因为轮转是周期性的left = nums[len(nums)-k:len(nums)]right = nums[0:len(nums)-k]nums[:] = left+rightreturn nums
参考:
class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not return anything, modify nums in-place instead."""def reverse(i, j):while i < j:nums[i], nums[j] = nums[j], nums[i]i += 1j -= 1n = len(nums)k %= n # 轮转 k 次等于轮转 k%n 次reverse(0, n - 1)reverse(0, k - 1)reverse(k, n - 1)
相关文章:

【hot100】刷题记录(6)-轮转数组
题目描述: 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转…...
Android createScaledBitmap与Canvas通过RectF drawBitmap生成马赛克/高斯模糊(毛玻璃)对比,Kotlin
Android createScaledBitmap与Canvas通过RectF drawBitmap生成马赛克/高斯模糊(毛玻璃)对比,Kotlin import android.graphics.Bitmap import android.graphics.BitmapFactory import android.graphics.Canvas import android.graphics.RectF …...

ThinkPad E480安装Ubuntu 18.04无线网卡驱动
个人博客地址:ThinkPad E480安装Ubuntu 18.04无线网卡驱动 | 一张假钞的真实世界 遗憾的是虽然下面的方法可以解决,但是内核升级后需要重新安装。 基本信息 Ubuntu 18.04ThinkPad E480使用下面的命令查看 Linux 内核: $ uname -r 5.0.0-3…...

自然语言处理——从原理、经典模型到应用
1. 概述 自然语言处理(Natural Language Processing,NLP)是一门借助计算机技术研究人类语言的科学,是人工智能领域的一个分支,旨在让计算机理解、生成和处理人类语言。其核心任务是将非结构化的自然语言转换为机器可以…...

Ollama 运行从 ModelScope 下载的 GGUF 格式的模型
本文系统环境 Windows 10 Ollama 0.5.7 Ollama 是什么? Ollama 可以让你快速集成和部署本地 AI 模型。它支持各种不同的 AI 模型,并允许用户通过简单的 API 进行调用 Ollama 的安装 Ollama 官网 有其下载及安装方法,非常简便 但如果希…...

Haproxy介绍及学习
一、负载均衡(load balance): 1.一种服务基于硬件设备实现的高可用反向代理技术,将特定的业务分担给指定的一个或者多个后端特定的服务器,提高了业务的并发处理能力保证业务的高可用并方便对业务后期的水平动态扩展性。 2.使用负载均衡的原因…...

【2024年华为OD机试】 (C卷,200分)- 贪心歌手(JavaScriptJava PythonC/C++)
一、问题描述 问题描述 一个歌手需要从A城前往B城参加演出,必须在T天内到达。途中会经过N座城市,且不能往回走。每两座城市之间的行程天数已知。歌手在每座城市都可以卖唱赚钱,但收入会随着停留天数的增加而递减。具体来说,第一…...

深度学习在金融风控中的应用:突破传统模型的瓶颈
深度学习在金融风控中的应用:突破传统模型的瓶颈 金融风险控制(简称“风控”)是现代金融体系中至关重要的一环,关系到金融机构的稳定性、客户的安全以及整体经济的健康运行。近年来,随着深度学习的迅猛发展,传统的风控模型正面临被颠覆的挑战,新的技术手段和思维方式正…...
 教程(4))
LLM - 大模型 ScallingLaws 的指导模型设计与实验环境(PLM) 教程(4)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/145323420 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 Scaling Laws (缩放法则) 是大模型领域中,用于描述 模型性能(Loss) 与…...

hunyuan 混元学习
使用了5个subset,也是用了text-image和text-video进行训练的 也是进行了复杂的视频选择。同movie gen. 也进行了模型切断,用拉普拉斯算子找到最清晰的一帧作为训练的起始 训练了不同的模型去选择数据,比如用Dover去选择美观度比较好的数据,…...

开发、科研工具汇总
一些基础教程网站 W3:w3school 在线教程 菜鸟:菜鸟教程 - 学的不仅是技术,更是梦想! 开发相关参考文档 Vue2:Vue.js Vue3:Vue.js - 渐进式 JavaScript 框架 | Vue.js MDN:MDN Web Docs HT…...
)
项目部署(springboot项目)
1、安装Nginx,并开启 2、前端项目打包:npm run build:prod--->dist 3、后端项目打包:install--->xxx.jar 4、开放需要的端口号:比如我的后端项目端口号为8282,则需要防火墙和服务器同时开发8282端口 5、将di…...

OpenEuler学习笔记(十四):在OpenEuler上搭建.NET运行环境
一、在OpenEuler上搭建.NET运行环境 基于包管理器安装 添加Microsoft软件源:运行命令sudo rpm -Uvh https://packages.microsoft.com/config/centos/8/packages-microsoft-prod.rpm,将Microsoft软件源添加到系统中,以便后续能够从该源安装.…...

神经网络的通俗介绍
人工神经网络,是一种模仿人类大脑工作原理的数学模型。人类的大脑是由无数的小“工作站”组成的,每个工作站叫做“神经元”。这些神经元通过“电线”互相连接,负责接收、处理和传递信息。 一、人类大脑神经网络 人类大脑的神经网络大概长这…...

基于 AWS SageMaker 对 DeepSeek-R1-Distilled-Llama-8B 模型的精调与实践
在当今人工智能蓬勃发展的时代,语言模型的性能优化和定制化成为研究与应用的关键方向。本文聚焦于 AWS SageMaker 平台上对 DeepSeek-R1-Distilled-Llama-8B 模型的精调实践,详细探讨这一过程中的技术细节、操作步骤以及实践价值。 一、实验背景与目标 …...

如何使用DeepSeek R1
以下是如何使用DeepSeek R1的详细步骤: ### 一、注册DeepSeek账户 1. **访问官方网站**: - 打开浏览器,访问[chat.deepseek.com](http://chat.deepseek.com)。 2. **注册账户**: - 使用电子邮件、Google账户或86手机号码…...

大屏 UI 设计风格的未来趋势
在科技飞速革新的时代,大屏设备的应用领域不断拓展,从城市的智能交通指挥中心,到商场的互动广告大屏,再到家庭的超大尺寸智能电视,大屏已然成为信息展示与交互的关键载体。大屏 UI 设计风格也随之不断演变,…...

unity学习22:Application类其他功能
目录 1 是否允许后台运行 1.1 Application.runInBackground,显示是否允许后台运行 1.2 设置的地方 2 打开URL 2.1 Application.OpenURL("") 打开超链接 3 退出游戏 3.1 Application.Quit() 退出游戏 4 场景相关 5 返回游戏状态 6 控制游戏的行…...

51单片机入门_02_C语言基础0102
C语言基础部分可以参考我之前写的专栏C语言基础入门48篇 以及《从入门到就业C全栈班》中的C语言部分,本篇将会结合51单片机讲差异部分。 课程主要按照以下目录进行介绍。 文章目录 1. 进制转换2. C语言简介3. C语言中基本数据类型4. 标识符与关键字5. 变量与常量6.…...

定位的叠放次序 z-index
浮动定位和绝对定位的区别: 浮动只会压住它下面标准流的盒子,但是不会压住下面标准流盒子里面的文字,但是绝对定位(固定定位)会压住下面标准流所有的内容。...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
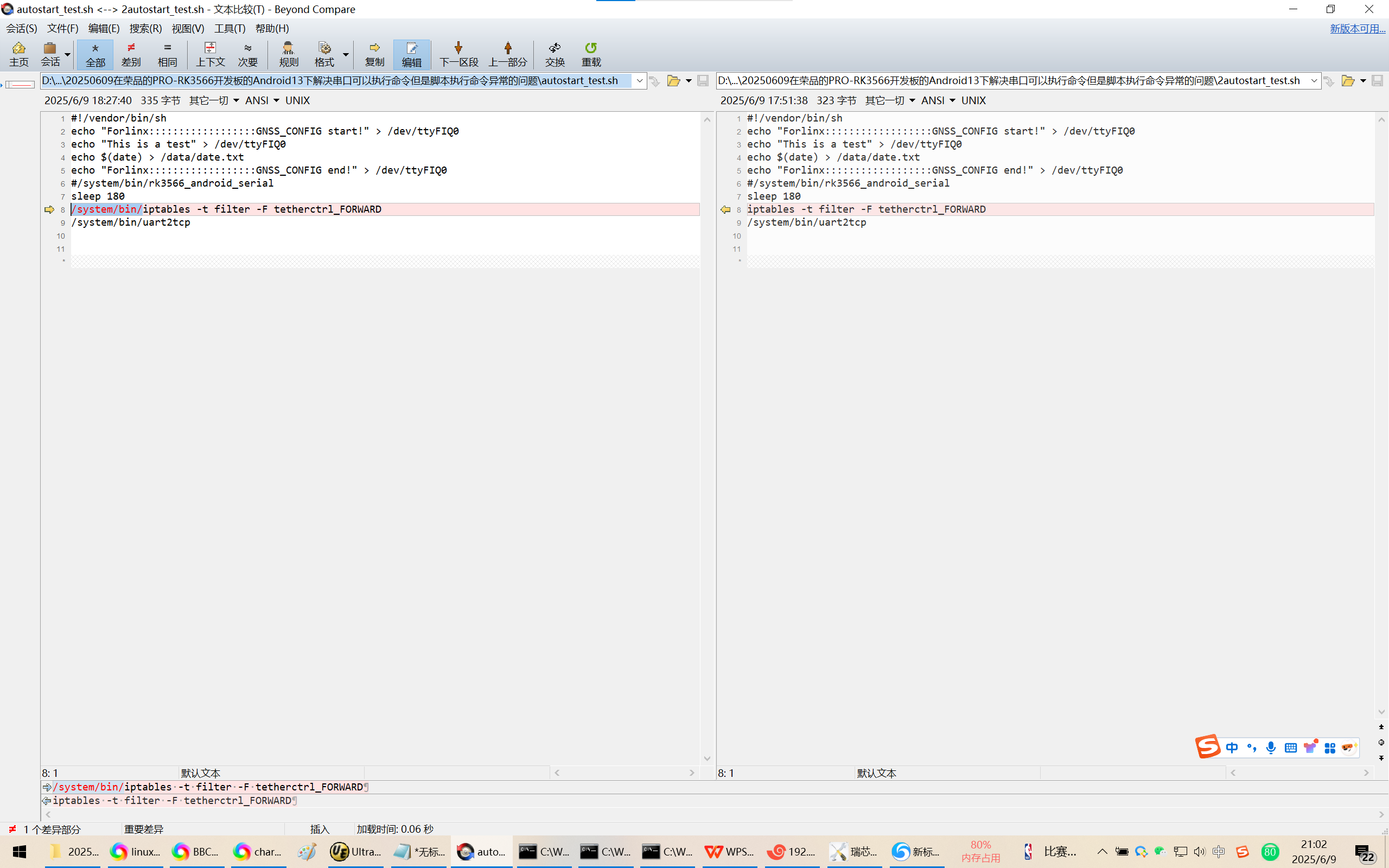
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...

软件工程教学评价
王海林老师您好。 您的《软件工程》课程成功地将宏观的理论与具体的实践相结合。上半学期的理论教学中,您通过丰富的实例,将“高内聚低耦合”、SOLID原则等抽象概念解释得十分透彻,让这些理论不再是停留在纸面的名词,而是可以指导…...
