【题解】AtCoder Beginner Contest ABC391 D Gravity
题目大意
- 原题面链接
在一个 1 0 9 × W 10^9\times W 109×W 的平面里有 N N N 个方块。我们用 ( x , y ) (x,y) (x,y) 表示第 x x x 列从下往上数的 y y y 个位置。第 i i i 个方块的位置是 ( x i , y i ) (x_i,y_i) (xi,yi)。现在执行无数次操作,每一次操作如下:
- 如果整个平面的最下面一行的 W W W 个位置上都有方块,那么把这一行的方块都消除掉。
- 从下往上遍历每一个未被消除的方块,如果它不在最下面一行且它下面是空格子,将它向下移动一格。注意:只移动一格!
思路
观察数据范围,需要预处理。我们不妨令 t i i ti_i tii 表示第 i i i 个方块什么时候被消除。对于无法被消除的方块,其 t i i ti_i tii 为极大值。我们可以拿样例来寻找突破口,样例解释里面的那个图片如下:
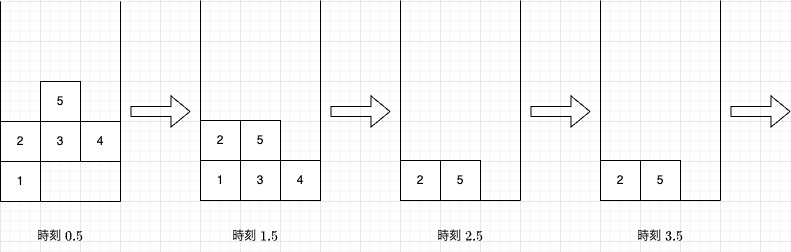
观察一下,第二次操作执行完和第三次操作执行完的结果是一样的,所以继续执行下去,结果不会改变。也就是说,第三次操作及以后的操作都是“无效操作”,而其中可以消除的操作只有第二次,我们将其称为“有意义”。稍加观察可以发现,有意义的操作数量是每一列方块数量的最小值,很容易证明出来。
每一次有意义的操作之前我们可能需要一些(有的时候不需要)操作来让所有方块掉到地上,这种操作我们称之为“预备操作”。不难发现,预备操作的结束时间是每一列最下面的方块的纵坐标的最大值减一。所以有意义的操作的结束时间就是每一列最下面的方块的纵坐标的最大值(有点绕),可以用来更新 t i i ti_i tii。
一个很重要的问题:怎么预处理每一列的那堆格子?开个 vector 数组,具体实现看代码。
那么在每一次询问的时候只要看 t i A j ti_{A_j} tiAj 与 T j T_j Tj 的大小关系即可。
预处理部分代码
其实有点小细节能 hack,见文末彩蛋。
for (int i = 1; i <= n; i++)
{cin >> x[i] >> y[i]; // 读入v[x[i]].push_back(i); // 这一列的方块ti[i] = 1e9 + 7; // 极大值
}
int mn = 1e9 + 7; // 极大值
for (int i = 1; i <= w; i++)
{int cnt = v[i].size(); // 强转一下// int 类型不能直接和 unsigned int 类型取 minmn = min(mn, cnt);
}
for (int i = 0; i < mn; i++)
{int mx = 0; // 计算最大值for (int j = 1; j <= w; j++)mx = max(mx, y[v[j][i]]);for (int j = 1; j <= w; j++)ti[v[j][i]] = mx; // 更新
}
完整代码
我的提交记录
时间复杂度分析
预处理里面有个双重循环,为什么没有超时呢? m n mn mn 最大为 N N N,复杂度理论上来说是 O ( N ⋅ W ) O(N\cdot W) O(N⋅W) 的,但是考虑到实际构造原因,其均摊时间复杂度是不会超时的,所以可以通过本题。
彩蛋
大框架没问题,有个小细节出锅了。请问题目保证输入按 y i y_i yi 升序排序了吗?没有!得自己排个序。注意一下,得用结构体排序,既可以让变量对应上,也可以存储初始下标。正确版本我还没写,应该没啥太大区别,遇到问题欢迎在评论里问我或私信沟通哦!要是有其他问题或者 hack 数据也可以联系我哦!
相关文章:

【题解】AtCoder Beginner Contest ABC391 D Gravity
题目大意 原题面链接 在一个 1 0 9 W 10^9\times W 109W 的平面里有 N N N 个方块。我们用 ( x , y ) (x,y) (x,y) 表示第 x x x 列从下往上数的 y y y 个位置。第 i i i 个方块的位置是 ( x i , y i ) (x_i,y_i) (xi,yi)。现在执行无数次操作,每一次…...
使用 SpringBoot+Thymeleaf 模板引擎进行 Web 开发
目录 一、什么是 Thymeleaf 模板引擎 二、Thymeleaf 模板引擎的 Maven 坐标 三、配置 Thymeleaf 四、访问页面 五、访问静态资源 六、Thymeleaf 使用示例 七、Thymeleaf 常用属性 前言 在现代 Web 开发中,模板引擎被广泛用于将动态内容渲染到静态页面中。Thy…...

【Java异步编程】CompletableFuture综合实战:泡茶喝水与复杂的异步调用
文章目录 一. 两个异步任务的合并:泡茶喝水二. 复杂的异步调用:结果依赖,以及异步执行调用等 一. 两个异步任务的合并:泡茶喝水 下面的代码中我们实现泡茶喝水。这里分3个任务:任务1负责洗水壶、烧开水,任…...

Nginx知识
nginx 精简的配置文件 worker_processes 1; # 可以理解为一个内核一个worker # 开多了可能性能不好events {worker_connections 1024; } # 一个 worker 可以创建的连接数 # 1024 代表默认一般不用改http {include mime.types;# 代表引入的配置文件# mime.types 在 ngi…...

Unity开发游戏使用XLua的基础
Unity使用Xlua的常用编码方式,做一下记录 1、C#调用lua 1、Lua解析器 private LuaEnv env new LuaEnv();//保持它的唯一性void Start(){env.DoString("print(你好lua)");//env.DoString("require(Main)"); 默认在resources文件夹下面//帮助…...

AI-ISP论文Learning to See in the Dark解读
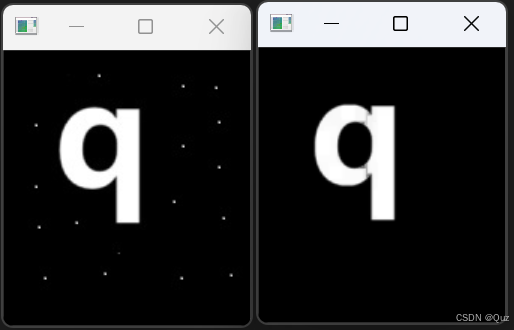
论文地址:Learning to See in the Dark 图1. 利用卷积网络进行极微光成像。黑暗的室内环境。相机处的照度小于0.1勒克斯。索尼α7S II传感器曝光时间为1/30秒。(a) 相机在ISO 8000下拍摄的图像。(b) 相机在ISO 409600下拍摄的图像。该图像存在噪点和色彩偏差。©…...
OpenCV:开运算
目录 1. 简述 2. 用腐蚀和膨胀实现开运算 2.1 代码示例 2.2 运行结果 3. 开运算接口 3.1 参数详解 3.2 代码示例 3.3 运行结果 4. 开运算应用场景 5. 注意事项 6. 总结 相关阅读 OpenCV:图像的腐蚀与膨胀-CSDN博客 OpenCV:闭运算-CSDN博客 …...

38. RTC实验
一、RTC原理详解 1、6U内部自带到了一个RTC外设,确切的说是SRTC。6U和6ULL的RTC内容在SNVS章节。6U的RTC分为LP和HP。LP叫做SRTC,HP是RTC,但是HP的RTC掉电以后数据就丢失了,即使用了纽扣电池也没用。所以必须要使用LP,…...

Flutter 新春第一弹,Dart 宏功能推进暂停,后续专注定制数据处理支持
在去年春节,Flutter 官方发布了宏(Macros)编程的原型支持, 同年的 5 月份在 Google I/O 发布的 Dart 3.4 宣布了宏的实验性支持,但是对于 Dart 内部来说,从启动宏编程实验开始已经过去了几年,但…...

巴菲特价值投资思想的核心原则
巴菲特价值投资思想的核心原则 关键词:安全边际、长期投资、内在价值、管理团队、经济护城河、简单透明 摘要:本文深入探讨了巴菲特价值投资思想的核心原则,包括安全边际、长期投资、企业内在价值、优秀管理团队、经济护城河和简单透明的业务…...

C 或 C++ 中用于表示常量的后缀:1ULL
1ULL 是一个在 C 或 C 中用于表示常量的后缀,它具体指示编译器将这个数值视为特定类型的整数。让我们详细解释一下: 1ULL 的含义 1: 这是最基本的部分,表示数值 1。U: 表示该数值是无符号(Unsigned)的。这意味着它只…...

vue3中el-input无法获得焦点的问题
文章目录 现象两次nextTick()加setTimeout()解决结论 现象 el-input被外层div包裹了,设置autofocus不起作用: <el-dialog v-model"visible" :title"title" :append-to-bodytrue width"50%"><el-form v-model&q…...

程序诗篇里的灵动笔触:指针绘就数据的梦幻蓝图<3>
大家好啊,我是小象٩(๑ω๑)۶ 我的博客:Xiao Xiangζั͡ޓއއ 很高兴见到大家,希望能够和大家一起交流学习,共同进步。 今天我们来对上一节做一些小补充,了解学习一下assert断言,指针的使用和传址调用…...

(三)QT——信号与槽机制——计数器程序
目录 前言 信号(Signal)与槽(Slot)的定义 一、系统自带的信号和槽 二、自定义信号和槽 三、信号和槽的扩展 四、Lambda 表达式 总结 前言 信号与槽机制是 Qt 中的一种重要的通信机制,用于不同对象之间的事件响…...

Qt 5.14.2 学习记录 —— 이십이 QSS
文章目录 1、概念2、基本语法3、给控件应用QSS设置4、选择器1、子控件选择器2、伪类选择器 5、样式属性box model 6、实例7、登录界面 1、概念 参考了CSS,都是对界面的样式进行设置,不过功能不如CSS强大。 可通过QSS设置样式,也可通过C代码…...

Hot100之哈希
1两数之和 题目 思路解析 解法1--两次循环 解法2--哈希表一次循环 代码 解法1--两次循环 class Solution {public int[] twoSum(int[] nums, int target) {int nums1[] new int[2];int length nums.length;for (int i 0; i < length; i) {for (int j i 1; j < …...

油漆面积——蓝桥杯
1.题目描述 X 星球的一批考古机器人正在一片废墟上考古。 该区域的地面坚硬如石、平整如镜。 管理人员为方便,建立了标准的直角坐标系。 每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。 经过各种测量,每个机器人都会报告一个或多个矩…...

深度解析:网站快速收录与服务器性能的关系
本文转自:百万收录网 原文链接:https://www.baiwanshoulu.com/37.html 网站快速收录与服务器性能之间存在着密切的关系。服务器作为网站运行的基础设施,其性能直接影响到搜索引擎对网站的抓取效率和收录速度。以下是对这一关系的深度解析&am…...

925.长按键入
目录 一、题目二、思路三、解法四、收获 一、题目 你的朋友正在使用键盘输入他的名字 name。偶尔,在键入字符 c 时,按键可能会被长按,而字符可能被输入 1 次或多次。 你将会检查键盘输入的字符 typed。如果它对应的可能是你的朋友的名字&am…...

JavaScript 中的 var 和 let :关键区别与使用建议
在 JavaScript 开发中,变量声明是基础且重要的部分。 var 和 let 都是用于声明变量的关键字,但它们在作用域、变量提升、重复声明等方面存在显著差异。本文将详细探讨它们的区别,并给出使用建议。 1. 作用域 1.1 var 的作用域 …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
