完全卸载mysql server步骤
1. 在控制面板中卸载mysql
2. 打开注册表,运行regedit, 删除mysql信息
HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->EventLog->Application->Mysql
HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->Mysql
3.删除Mysql安装信息。
(1) C:\Documents and Settings\All Users\Application Data\Mysql
(2)删除Mysql安装目录,默认在C盘。找不到的话可以搜my.ini
4.重启电脑后,重新安装Mysql Server即可。
相关文章:

完全卸载mysql server步骤
1. 在控制面板中卸载mysql 2. 打开注册表,运行regedit, 删除mysql信息 HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->EventLog->Application->Mysql HKEY_LOCAL_MACHINE-> SYSTEM->CurrentContolSet->Services->Mysql …...
)
C#方法(练习)
1.定义一个函数,输入三个值,找出三个数中的最小值 2.定义一个函数,输入三个值,找出三个数中的最大值 3.定义一个函数,输入三个值,找出三个数中的平均值 4.定义一个函数,计算一个数的 N 次方 Pow(2, 3)返回8 5.传入十一…...
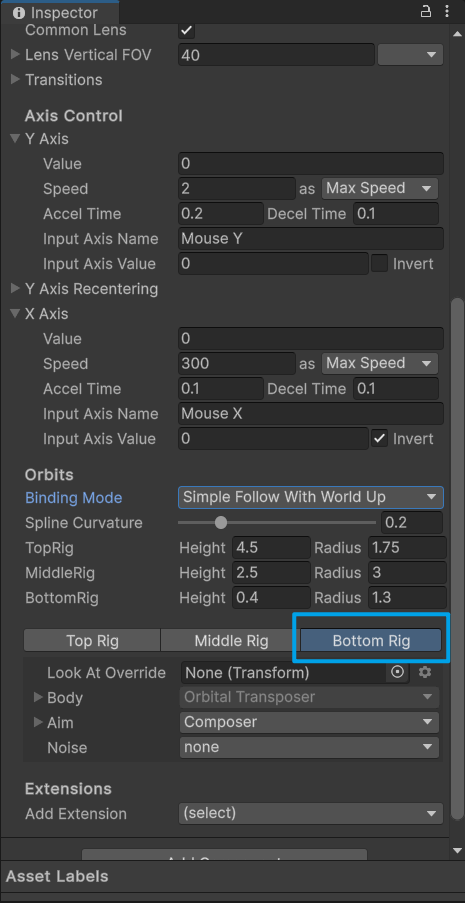
Unity游戏(Assault空对地打击)开发(3) 摄像机的控制
详细步骤 打开My Assets或者Package Manager。 选择Unity Registry。 搜索Cinemachine,找到 Cinemachine包,点击 Install按钮进行安装。 关闭窗口,新建一个FreeLook Camera,如下。 接着新建一个对象Pos,拖到Player下面…...

ChatGPT-4o和ChatGPT-4o mini的差异点
在人工智能领域,OpenAI再次引领创新潮流,近日正式发布了其最新模型——ChatGPT-4o及其经济实惠的小型版本ChatGPT-4o Mini。这两款模型虽同属于ChatGPT系列,但在性能、应用场景及成本上展现出显著的差异。本文将通过图文并茂的方式࿰…...

SQL进阶实战技巧:某芯片工厂设备任务排产调度分析 | 间隙分析技术应用
目录 0 技术定义与核心原理 1 场景描述 2 数据准备 3 间隙分析法 步骤1:原始时间线可视化...

【力扣】438.找到字符串中所有字母异位词
AC截图 题目 思路 我一开始是打算将窗口内的s子字符串和p字符串都重新排序,然后判断是否相等,再之后进行窗口滑动。不过缺点是会超时。 class Solution { public:vector<int> findAnagrams(string s, string p) {vector<int> vec;if(s.siz…...
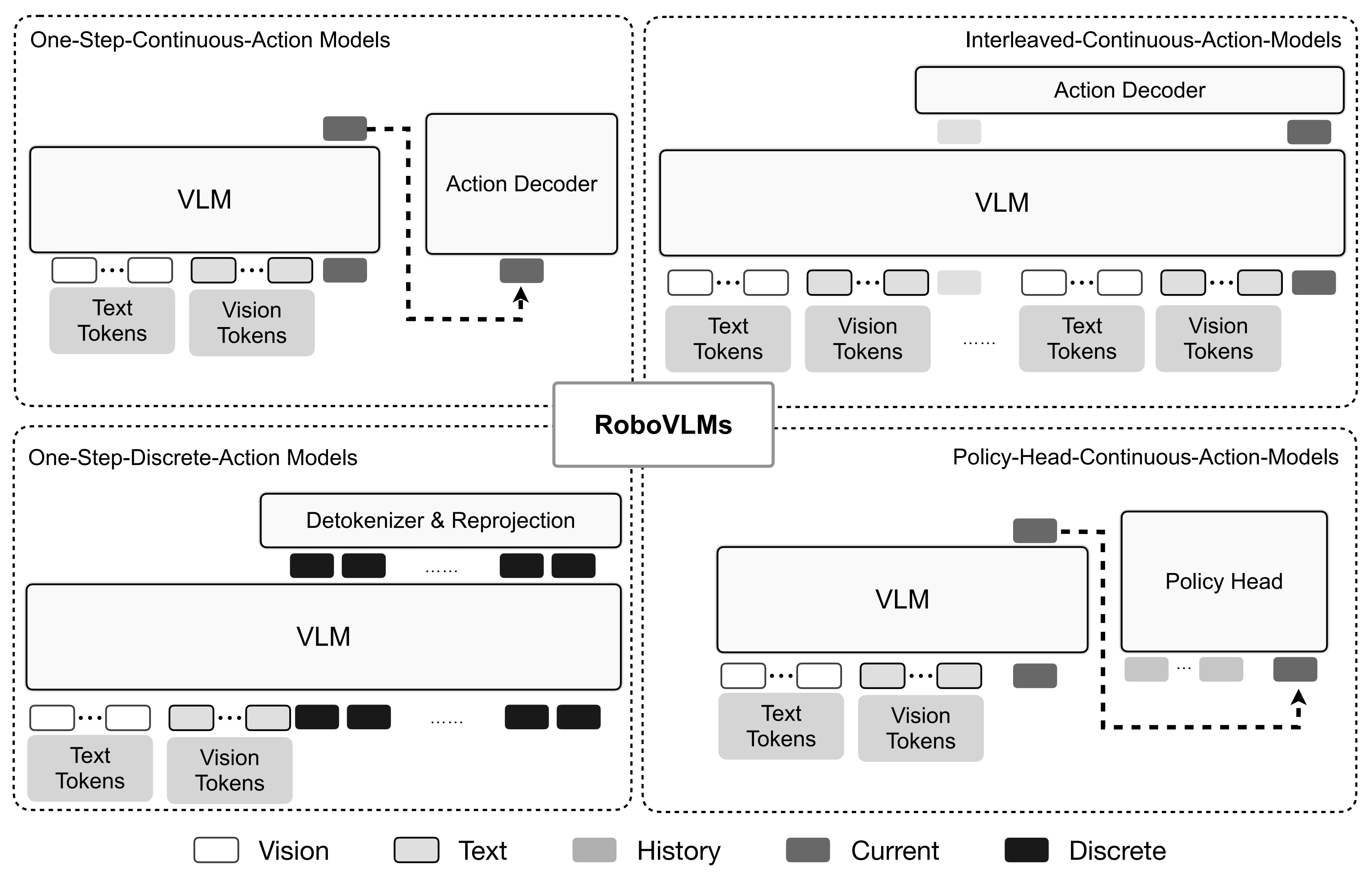
2024具身智能模型汇总:从训练数据、动作预测、训练方法到Robotics VLM、VLA
前言 本文一开始是属于此文《GRAPE——RLAIF微调VLA模型:通过偏好对齐提升机器人策略的泛化能力》的前言内容之一(该文发布于23年12月底),但考虑到其重要性,加之那么大一张表格 看下来 阅读体验较差,故抽出取来独立成文且拆分之 …...

Day33【AI思考】-函数求导过程 的优质工具和网站
文章目录 **函数求导过程** 的优质工具和网站**一、动态图形工具**1. **Desmos(网页端)**2. **GeoGebra(全平台)** **二、分步推导工具**3. **Wolfram Alpha(网页/App)**4. **Symbolab(网页/App…...
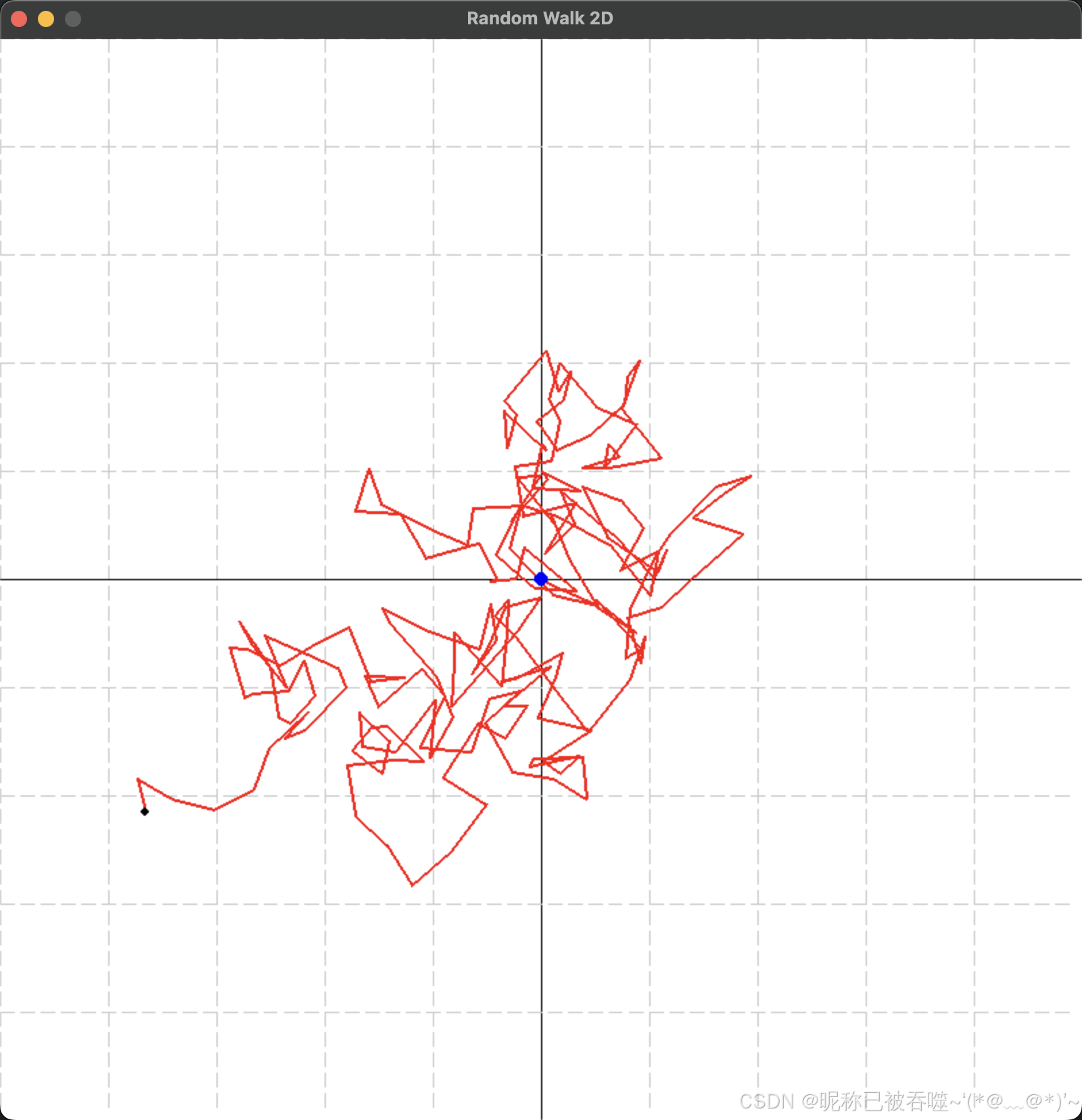
【URL】一个简单基于Gym的2D随机游走环境,用于无监督强化学习(URL)
import gym from gym import spaces import numpy as np import pygameclass RandomWalk2DEnv(gym.Env):def __init__(self):super(RandomWalk2DEnv, self).__init__()# 定义状态空间为2D坐标(x, y)self.x_min, self.x_max -10, 10 # 更新尺寸为 (-10,…...

【VM】VirtualBox安装ubuntu22.04虚拟机
阅读本文之前,请先根据 安装virtualbox 教程安装virtulbox虚拟机软件。 1.下载Ubuntu系统镜像 打开阿里云的镜像站点:https://developer.aliyun.com/mirror/ 找到如图所示位置,选择Ubuntu 22.04.3(destop-amd64)系统 Ubuntu 22.04.3(desto…...
函数的使用问题)
MySQL的GROUP BY与COUNT()函数的使用问题
在MySQL中,GROUP BY和 COUNT()函数是数据聚合查询中非常重要的工具。正确使用它们可以有效地统计和分析数据。然而,不当的使用可能会导致查询结果不准确或性能低下。本文将详细讨论 GROUP BY和 COUNT()函数的使用方法及常见问题,并提供相应的…...
)
C# 精炼题18道题(类,三木运算,Switch,计算器)
1.数组元素和 2.数组元素乘积 3.数组元素平均数 4.数组中最大值 5.数组中的偶数 6.数组中的阶乘 7.数组反转 8.字符串反转 9.回文字符串 10.检查回文 11.最小最大值 12.找素数 13.字符串中的最长无重复字符串 14.字符串去重 15.数组中计算两数之和 16.数字到字符…...

96,【4】 buuctf web [BJDCTF2020]EzPHP
进入靶场 查看源代码 GFXEIM3YFZYGQ4A 一看就是编码后的 1nD3x.php 访问 得到源代码 <?php // 高亮显示当前 PHP 文件的源代码,用于调试或展示代码结构 highlight_file(__FILE__); // 关闭所有 PHP 错误报告,防止错误信息泄露可能的安全漏洞 erro…...

数据库 - Sqlserver - SQLEXPRESS、由Windows认证改为SQL Server Express认证进行连接 (sa登录)
本文讲SqlServer Express版本在登录的时候, 如何由Windows认证,修改为Sql Server Express认证。 目录 1,SqlServer Express的Windows认证 2,修改为混合认证 3,启用sa 用户 4,用sa 用户登录 下面是详细…...

2025年02月02日Github流行趋势
项目名称:oumi 项目地址url:https://github.com/oumi-ai/oumi 项目语言:Python 历史star数:1416 今日star数:205 项目维护者:xrdaukar, oelachqar, taenin, wizeng23, kaisopos 项目简介:构建最…...
)
【数据分析】案例03:当当网近30日热销图书的数据采集与可视化分析(scrapy+openpyxl+matplotlib)
当当网近30日热销图书的数据采集与可视化分析(scrapy+openpyxl+matplotlib) 当当网近30日热销书籍官网写在前面 实验目的:实现当当网近30日热销图书的数据采集与可视化分析。 电脑系统:Windows 使用软件:Visual Studio Code Python版本:python 3.12.4 技术需求:scrapy、…...

如何使用 DeepSeek 和 Dexscreener 构建免费的 AI 加密交易机器人?
我使用DeepSeek AI和Dexscreener API构建的一个简单的 AI 加密交易机器人实现了这一目标。在本文中,我将逐步指导您如何构建像我一样的机器人。 DeepSeek 最近发布了R1,这是一种先进的 AI 模型。您可以将其视为 ChatGPT 的免费开源版本,但增加…...

buu-jarvisoj_level0-好久不见30
嘶,我咋觉得这个也是栈溢出呢,找到读取的值,在再找到后门函数...
深度学习查漏补缺:1.梯度消失、梯度爆炸和残差块
一、梯度消失 梯度消失的根本原因在于 激活函数的性质和链式法则的计算: 激活函数的导数很小: 常见的激活函数(例如 Sigmoid 和 Tanh)在输入较大或较小时,输出趋于饱和(Sigmoid 的输出趋于 0 或 1…...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】2.2 多维数组切片:跨步访问与内存布局
2.2 多维数组切片:跨步访问与内存布局 目录/提纲 #mermaid-svg-FbBIOMVivQfdX2LJ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-FbBIOMVivQfdX2LJ .error-icon{fill:#552222;}#mermaid-svg-FbBIOMVivQ…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
