【算法精练】二分查找算法总结
目录
前言
1. 二分查找(基础版)
2. 寻找左右端点
循环判断条件
求中间点
总结
前言
说起二分查找,也是一种十分常见的算法,最常听说的就是:二分查找只能在数组有序的场景下使用;其实也未必,只要能找到规律,也依然可以使用;本文我将分享一些有关二分查找算法的做题经验;

1. 二分查找(基础版)
注意:二分查找算法也并非是只能在数组有序的场景下使用,只要数据具有 " 二段性 " 就可以使用;
基础版的二分查找,没有那么多弯弯绕绕,以及边界情况;下面是一个基础版本的示例:
while( left <= right)
{int mid = left + (right - left) / 2;if(nums[mid] > target) right = mid - 1;else if(nums[mid] < target) left = mid + 1;else return mid;
}在计算中间点时比较推荐示例中的写法:
int mid = left + (right - left) / 2;这种方式可以有效的防止数据溢出;
由此可以总结出基础版本的二分模板:
while( left <= right)
{int mid = left + (right - left) / 2;if(...) right = mid -1;else if(...) left = mid + 1;else return ...;
}2. 寻找左右端点
这种方式的二分算法有比较经典的题目:
力扣中的第34道题:

这种类型再使用基础版本的二分就没法很好的解决:
使用基础版本只能找到一组目标值中的某一个,比如:
nums = [5,7,8,8,8,9]; // target = 8基础版本只能保证找到数组中的8(目标值),但是要知道目标值开始位置和解释位置就不行了;还需要进行一些操作,但这样就容易让时间复杂度降到 O(N),也就是所有值都是目标值的情况;因此基础版本在这道题中并不是最优解;这时就可以使用二分的进阶版:寻找区间左右端点;
怎么找左右端点?
还是使用这个示例:
nums = [5,7,8,8,8,9];寻找端点版本,主要分成两种情况(设中间点为x):
以寻找左端点为例(以下的示例都是以求左端点):
- x < target:left = mid + 1;在区间[left,right]中找;
- x >= target:right = mid;

将数组划分成两个区间;right为什么是等于mid就一目了然了;

当mid在如图的位置时,如果right = mid + 1;那么剩下的区间就不会有target;
较为难的点就是细节的处理,这里很容易出错,一旦出错就会成死循环;
细节:求中间点、循环条件
循环判断条件
判断条件是:
while(left < right){...
}不需要判断是否相等,如果判断了就会死循环;
- x < target:left = mid + 1;
- x >= target:right = mid;
比如:

如果right == left时还进入循环判断,此时走的是 x >= target;right还是会在原来的位置;这样就会造成死循环;
求中间点
求中间点有两种:
// 第一种
mid = left + (right - left) / 2;// 第二种
mid = left + (right - left + 1) / 2;他们的区别在于当数组元素为偶数的时候:
第一种:

第二种:

求左端点只能使用第一种,否则也会造成死循环:
如果是第二种情况:
假设区间只剩两个端点:

使用第二种方法计算出的mid是右边的端点;那么当满足 x < target:left = mid + 1;时循环退出;如果满足的是 x >= target:right = mid;就会出现死循环;
而第一种:

当满足 x < target:left = mid + 1;时 left走到right位置,循环结束;
当满足的是 x >= target:right = mid;right走到mid位置(也就是left位置),循环结束;
总结一下:
// 寻找左端点
while(left < right) {int mid = left + (right - left) / 2;if(left < target) left = mid + 1;else right = mid;
}// 寻找右端点
while(left < right) {int mid = left + (right - left + 1) / 2;if(right > target) right = mid - 1;else left = mid;
}可以得出模板:
// 寻找左端点
while(left < right) {int mid = left + (right - left) / 2;if(...) left = mid + 1;else right = mid;
}// 寻找右端点
while(left < right) {int mid = left + (right - left + 1) / 2;if(...) right = mid - 1;else left = mid;
}提醒:注意本文对二分进行了模板的总结,切记不要一味的记忆模板,要基于理解去使用;
以下是一些题目练习:
x的平方根
在排序数组中查找元素的第一个和最后一个位置
山脉数组的峰顶索引
总结
以上便是本文的全部内容,希望对你有所帮助,最后感谢阅读!
相关文章:

【算法精练】二分查找算法总结
目录 前言 1. 二分查找(基础版) 2. 寻找左右端点 循环判断条件 求中间点 总结 前言 说起二分查找,也是一种十分常见的算法,最常听说的就是:二分查找只能在数组有序的场景下使用;其实也未必,…...

从零开始实现一个双向循环链表:C语言实战
文章目录 1链表的再次介绍2为什么选择双向循环链表?3代码实现:从初始化到销毁1. 定义链表节点2. 初始化链表3. 插入和删除节点4. 链表的其他操作5. 打印链表和判断链表是否为空6. 销毁链表 4测试代码5链表种类介绍6链表与顺序表的区别7存储金字塔L0: 寄存…...

MYSQL面试题总结(题目来源JavaGuide)
MYSQL基础架构 问题1:一条 SQL语句在MySQL中的执行过程 1. 解析阶段 (Parsing) 查询分析:当用户提交一个 SQL 语句时,MySQL 首先会对语句进行解析。这个过程会检查语法是否正确,确保 SQL 语句符合 MySQL 的语法规则。如果发现…...

visual studio安装
一、下载Visual Studio 访问Visual Studio官方网站。下载 Visual Studio Tools - 免费安装 Windows、Mac、Linux 在主页上找到并点击“下载 Visual Studio”按钮。 选择适合需求的版本,例如“Visual Studio Community”(免费版本)&#x…...

JVM执行引擎
一、执行引擎的概述: 执行引擎是]ava虚拟机核心的组成部分之一; “虚拟机”是一个相对于“物理机”的概念,这两种机器都有代码执行能力,其区别是物理机的执行引擎是直接建立在处理器、缓存、指令集和操作系统层面上的,而虚拟机的执行引擎则…...

C# 9.0记录类型:解锁开发效率的魔法密码
一、引言:记录类型的神奇登场 在 C# 的编程世界中,数据结构就像是构建软件大厦的基石,其重要性不言而喻。然而,传统的数据结构定义方式,尤其是在处理简单的数据承载对象时,常常显得繁琐复杂。例如…...

搭建自己的专属AI——使用Ollama+AnythingLLM+Python实现DeepSeek本地部署
前言 最近DeepSeek模型非常火,其通过对大模型的蒸馏得到的小模型可以较轻松地在个人电脑上运行,这也使得我们有机会在本地构建一个专属于自己的AI,进而把AI“调教”为我们希望的样子。本篇文章中我将介绍如何使用OllamaAnythingLLMPython实现…...

『 C++ 』中理解回调类型在 C++ 中的使用方式。
文章目录 案例 1:图形绘制库中的回调使用场景说明代码实现代码解释 案例 2:网络服务器中的连接和消息处理回调场景说明代码实现代码解释 案例 3:定时器中的回调使用场景说明代码实现代码解释 以下将通过不同场景给出几个使用回调类型的具体案…...

git多人协作
目录 一、项目克隆 二、 1、进入克隆仓库设置 2、协作处理 3、冲突处理 4、多人协作分支的推送拉取删除 1、分支推送(2种) 2、远程分支拉取(2种) 3、远程分支删除 一、项目克隆 git clone 画船听雨眠/test1 (自定义的名…...

CTFSHOW-WEB入门-命令执行71-77
题目:web 71 题目:解题思路:分析可知highlight_file() 函数被禁了,先想办法看看根目录:cvar_export(scandir(dirname(‘/’))); 尝试一下发现很惊奇:(全是?)这种情况我也…...

浅谈《图解HTTP》
感悟 滑至尾页的那一刻,内心突兀的涌来一阵畅快的感觉。如果说从前对互联网只是懵懵懂懂,但此刻却觉得她是如此清晰而可爱的呈现在哪里。 介绍中说,《图解HTTP》适合作为第一本网络协议书。确实,它就像一座桥梁,连接…...

LLMs瞬间获得视觉与听觉感知,无需专门训练:Meta的创新——在图像、音频和视频任务上实现最优性能。
引言: 问题: 当前的多模态任务(如图像、视频、音频描述生成、编辑、生成等)通常需要针对特定任务训练专门的模型,而现有的方法在跨模态泛化方面存在局限性,难以适应新任务。此外,多模态嵌入反演…...

自研有限元软件与ANSYS精度对比-Bar3D2Node三维杆单元模型-央视大裤衩实例
目录 1、“央视大裤衩”自研有限元软件求解 1.1、选择单元类型 1.2、导入“央视大裤衩”工程 1.3、节点坐标定义 1.4、单元连接关系、材料定义 1.5、约束定义 1.6、外载定义 1.7、矩阵求解 1.8、变形云图展示 1.9、节点位移 1.10、单元应力 1.11、节点支反力 2、“…...

kubernetes 高可用集群搭建
在生产环境中部署 Kubernetes 集群时,确保其高可用性(High Availability, HA)是至关重要的。高可用性不仅意味着减少服务中断时间,还能提高系统的稳定性和可靠性。本文将详细介绍如何搭建一个高可用的 Kubernetes 集群,…...

【C++】STL——vector底层实现
目录 💕 1.vector三个核心 💕2.begin函数,end函数的实现(简单略讲) 💕3.size函数,capacity函数的实现 (简单略讲) 💕4.reserve函数实现 (细节…...

数据结构初探:链表之单链表篇
本文图皆为作者手绘,所有代码基于vs2022运行测试 系列文章目录 数据结构初探:顺序表篇 文章目录 系列文章目录前言一、链表基础概念二、链表的分类简化边界条件处理使代码更清晰简洁提高程序稳定性 1.单链表(不带头不循环的单链表);1.1存储结构;1.2准备工作1.3链表增删查改的实…...

介绍一下Mybatis的底层原理(包括一二级缓存)
表面上我们的就是Sql语句和我们的java对象进行映射,然后Mapper代理然后调用方法来操作数据库 底层的话我们就涉及到Sqlsession和Configuration 首先说一下SqlSession, 它可以被视为与数据库交互的一个会话,用于执行 SQL 语句(Ex…...

Linux基础 ——tmux vim 以及基本的shell语法
Linux 基础 ACWING y总的Linux基础课,看讲义作作笔记。 tmux tmux 可以干嘛? tmux可以分屏多开窗口,可以进行多个任务,断线,不会自动杀掉正在进行的进程。 tmux – session(会话,多个) – window(多个…...

64位的谷歌浏览器Chrome/Google Chrome
64位的谷歌浏览器Chrome/Google Chrome 在百度搜索关键字:chrome,即可下载官方的“谷歌浏览器Chrome/Google Chrome”,但它可能是32位的(切记注意网址:https://www.google.cn/...., 即:google.cnÿ…...

jetson编译torchvision出现 No such file or directory: ‘:/usr/local/cuda/bin/nvcc‘
文章目录 1. 完整报错2. 解决方法 1. 完整报错 jetson编译torchvision,执行python3 setup.py install --user遇到报错 running build_ext error: [Errno 2] No such file or directory: :/usr/local/cuda/bin/nvcc完整报错信息如下: (pytorch) nxnx-desktop:~/Do…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
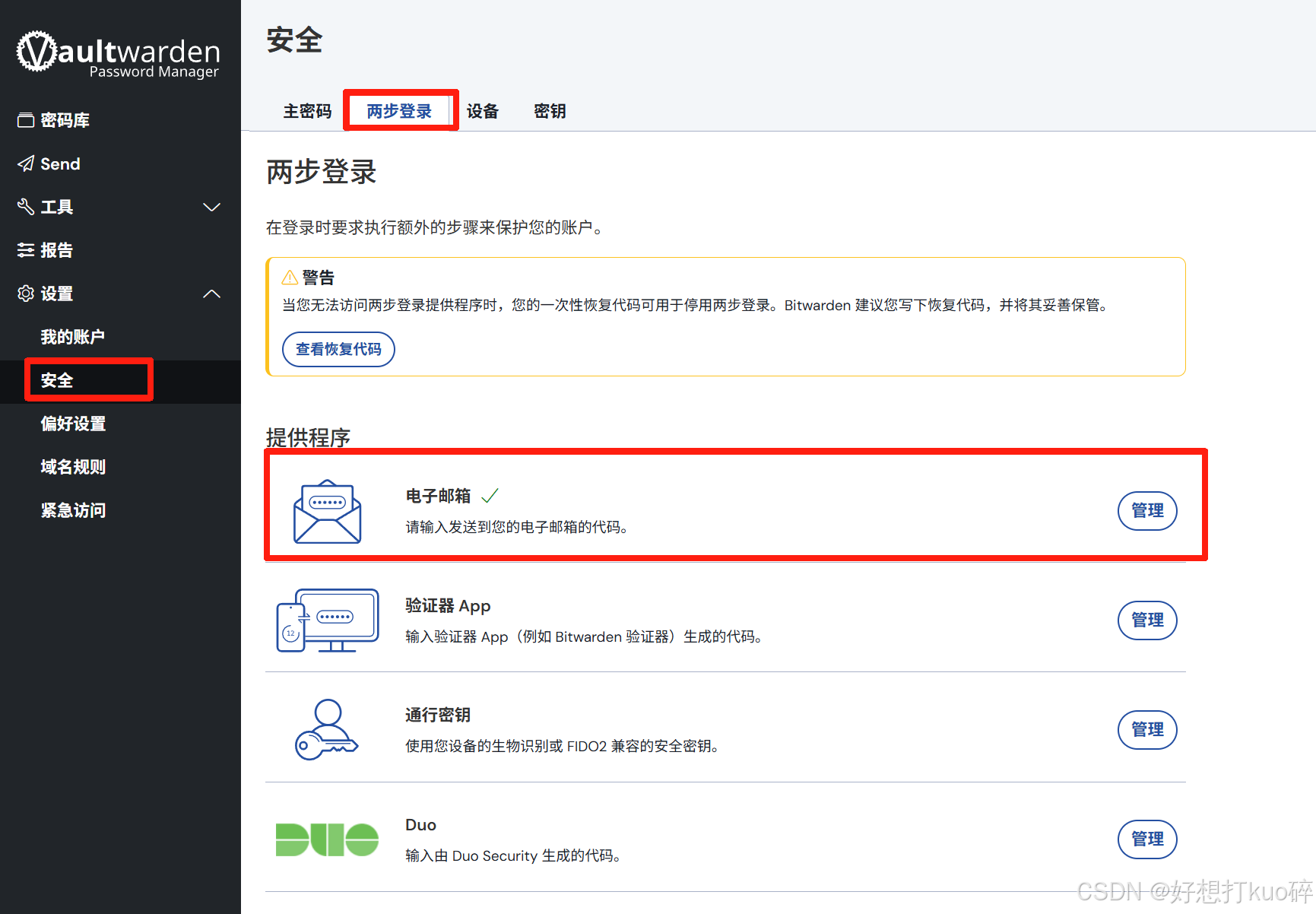
轻量安全的密码管理工具Vaultwarden
一、Vaultwarden概述 Vaultwarden主要作用是提供一个自托管的密码管理器服务。它是Bitwarden密码管理器的第三方轻量版,由国外开发者在Bitwarden的基础上,采用Rust语言重写而成。 (一)Vaultwarden镜像的作用及特点 轻量级与高性…...
