LeetCode - Google 大模型10题 第2天 Position Embedding(位置编码) 3题
欢迎关注我的CSDN:https://spike.blog.csdn.net/
本文地址:https://spike.blog.csdn.net/article/details/145454489

在 Transformer 架构中,位置编码(Position Embedding) 是辅助模型理解序列中元素顺序的关键机制。绝对位置编码(Absolute Positional Encoding, Absolute PE) 是最基础的形式,通过为序列中的每个位置分配一个固定的、与位置相关的向量来注入位置信息,这些向量通常是通过正弦和余弦函数生成的,使模型明确区分不同位置的元素。相对位置编码(Relative Positional Encoding, Relative PE) 通过考虑元素之间的相对距离,使得模型在计算注意力时动态地捕捉序列中元素的相对位置关系。旋转位置编码(Rotary Positional Encoding, RoPE) 是相对位置编码的一种改进形式,通过将位置信息嵌入到查询(Query)和键(Key)向量中,以旋转的方式结合位置信息,使得模型在处理长序列时能够更高效地利用位置信息,同时保持计算的简洁性和可扩展性。
原理参考:理解 旋转位置编码(RoPE) 与 绝对相对位置编码 之间的优势
1. 旋转位置编码 RoPE
旋转位置编码(Rotary Position Embedding, RoPE) 公式,在 Llama3 源码中,超参数 θ = 500000 \theta = 500000 θ=500000, p o s pos pos 是序列 s s s 的位置, i i i 是模型维度 d i m dim dim 的位置(或 d i m / 2 dim/2 dim/2),即:
P E ( p o s , i ) = c o s ( p o s 50000 0 i d m ) + i ⋅ s i n ( p o s 50000 0 i d m ) x i = 1 50000 0 i d m P E ( p o s , i ) = c o s ( p o s ⋅ x i ) + i ⋅ s i n ( p o s ⋅ x i ) = e i ⋅ p o s ⋅ x i PE_{(pos,i)} = cos(\frac{pos}{500000^{\frac{i}{d_{m}}}})+i\cdot sin(\frac{pos}{500000^{\frac{i}{d_{m}}}}) \\ x_{i} = \frac{1}{500000^{\frac{i}{d_{m}}}} \\ PE_{(pos,i)} = cos(pos \cdot x_{i})+i\cdot sin(pos \cdot x_{i})=e^{i \cdot pos \cdot x_{i}} PE(pos,i)=cos(500000dmipos)+i⋅sin(500000dmipos)xi=500000dmi1PE(pos,i)=cos(pos⋅xi)+i⋅sin(pos⋅xi)=ei⋅pos⋅xi
import math
import torch
import torch.nn.functional as F
from torch import nn
def precompute_freqs_cis(seq_len, dim, theta=10000.0):"""计算 freqs_cis, 即 频率(frequencies) + cis(cos isin)"""half_dim = dim // 2 # RoPE的维度是极坐标,是dim的1/2freqs = 1.0 / (theta ** (torch.arange(0, half_dim) / half_dim))t = torch.arange(seq_len) # type: ignorefreqs = torch.outer(t, freqs) # type: ignorefreqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64return freqs_cis
def apply_rotary_emb(q, k, freqs_cis):# [2, 8, 10, 64] -> [2, 8, 10, 32] (complex)xq = torch.view_as_complex(q.reshape(*q.shape[:-1], -1, 2)) # 转换成 complex 形式xk = torch.view_as_complex(k.reshape(*k.shape[:-1], -1, 2)) # 转换成 complex 形式# [2, 8, 10, 32, 2] -> [2, 8, 10, 64]xq_out = torch.view_as_real(xq * freqs_cis).flatten(3) # flatten 第3维度xk_out = torch.view_as_real(xk * freqs_cis).flatten(3)return xq_out, xk_out
class MultiHeadAttention(nn.Module):"""多头自注意力机制 MultiHeadAttention"""def __init__(self, heads, d_model, dropout=0.1):super().__init__()self.d_model = d_modelself.d_k = d_model // headsself.h = headsself.q_linear = nn.Linear(d_model, d_model)self.k_linear = nn.Linear(d_model, d_model)self.v_linear = nn.Linear(d_model, d_model)self.out = nn.Linear(d_model, d_model)self.dropout = nn.Dropout(dropout)@staticmethoddef attention(q, k, v, d_k, mask=None, dropout=None):scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)# 掩盖掉那些为了填补长度增加的单元,使其通过 softmax 计算后为 0if mask is not None:mask = mask.unsqueeze(1)scores = scores.masked_fill(mask == 0, -1e9)scores = F.softmax(scores, dim=-1)if dropout is not None:scores = dropout(scores)output = torch.matmul(scores, v)return outputdef forward(self, q, k, v, mask=None):bs = q.size(0)s = q.size(1)# 进行线性操作划分为成 h 个头k = self.k_linear(k).view(bs, -1, self.h, self.d_k)q = self.q_linear(q).view(bs, -1, self.h, self.d_k)v = self.v_linear(v).view(bs, -1, self.h, self.d_k)# 矩阵转置k = k.transpose(1, 2) # [bs,h,s,d] = [2, 8, 10, 64]q = q.transpose(1, 2)v = v.transpose(1, 2)# 预计算 RoPE 频率freqs_cis = precompute_freqs_cis(s, self.d_k) # output: [10, 32], i.e. [s,d_k//2]# 应用 RoPE 到 q 和 kq, k = apply_rotary_emb(q, k, freqs_cis)# 计算 attentionattn = self.attention(q, k, v, self.d_k, mask, self.dropout)# 连接多个头并输入到最后的线性层concat = attn.transpose(1, 2).contiguous().view(bs, -1, self.d_model)output = self.out(concat)return output
def main():# 设置超参数bs, s, h, d = 2, 10, 8, 512dropout_rate = 0.1# 创建 MultiHeadAttention 实例attention = MultiHeadAttention(h, d, dropout_rate)# 创建随机输入张量q = torch.randn(bs, s, d)k = torch.randn(bs, s, d)v = torch.randn(bs, s, d)# 可选:创建掩码,因果掩码,上三角矩阵mask = torch.tril(torch.ones(bs, s, s))# 测试无掩码的情况output_no_mask = attention(q, k, v)print("Output shape without mask:", output_no_mask.shape)# 测试有掩码的情况output_with_mask = attention(q, k, v, mask)print("Output shape with mask:", output_with_mask.shape)# 检查输出是否符合预期assert output_no_mask.shape == (bs, s, d), "Output shape is incorrect without mask"assert output_with_mask.shape == (bs, s, d), "Output shape is incorrect with mask"print("Test passed!")
if __name__ == '__main__':main()
2. 绝对位置编码 Absolute PE
Transformer 的 绝对位置编码(Absolute Positional Encoding) 公式,在 Transformer 源码中,超参数 θ = 10000 \theta = 10000 θ=10000, p o s pos pos 是序列 s s s 的位置, i i i 是模型维度 d i m dim dim 的位置,即:
P E ( p o s , 2 i ) = s i n ( p o s 1000 0 2 i d m ) P E ( p o s , 2 i + 1 ) = c o s ( p o s 1000 0 2 i d m ) A t t e n t i o n ( Q K V ) = S o f t m a x ( ( Q + P E ) ( K + P E ) ⊤ d m ) ( V + P E ) PE_{(pos,2i)}=sin(\frac{pos}{10000^{\frac{2i}{d_{m}}}}) \\ PE_{(pos,2i+1)}=cos(\frac{pos}{10000^{\frac{2i}{d_{m}}}}) \\ Attention(QKV) = Softmax(\frac{(Q+PE)(K+PE)^{\top}}{\sqrt{d_{m}}})(V+PE) PE(pos,2i)=sin(10000dm2ipos)PE(pos,2i+1)=cos(10000dm2ipos)Attention(QKV)=Softmax(dm(Q+PE)(K+PE)⊤)(V+PE)
注意:在多头自注意力机制中,位置编码的维度是 d m d_{m} dm,直接加到输入 x ( q , k , v ) x(q,k,v) x(q,k,v),再进行线性变换(Linear),划分成多个 head 和 d k d_{k} dk 维度。
import math
import torch
import torch.nn.functional as F
from torch import nn
def get_positional_encoding(seq_len, dim, theta=10000.0):"""计算 sin - cos 形式的绝对位置编码"""position = torch.arange(0, seq_len)# 优化写法# div_term = torch.exp(torch.arange(0, dim, 2) * -(math.log(theta) / dim))div_term = 1.0 / torch.pow(theta, torch.arange(0, dim, 2) / dim)pe = torch.zeros(seq_len, dim)pe[:, 0::2] = torch.sin(torch.outer(position, div_term))pe[:, 1::2] = torch.cos(torch.outer(position, div_term))return pe
class MultiHeadAttention(nn.Module):"""多头自注意力机制 MultiHeadAttention"""def __init__(self, heads, d_model, dropout=0.1):super().__init__()self.d_model = d_modelself.d_k = d_model // headsself.h = headsself.q_linear = nn.Linear(d_model, d_model)self.k_linear = nn.Linear(d_model, d_model)self.v_linear = nn.Linear(d_model, d_model)self.out = nn.Linear(d_model, d_model)self.dropout = nn.Dropout(dropout)@staticmethoddef attention(q, k, v, d_k, mask=None, dropout=None):scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)# 掩盖掉那些为了填补长度增加的单元,使其通过 softmax 计算后为 0if mask is not None:mask = mask.unsqueeze(1)scores = scores.masked_fill(mask == 0, -1e9)scores = F.softmax(scores, dim=-1)if dropout is not None:scores = dropout(scores)output = torch.matmul(scores, v)return outputdef forward(self, q, k, v, mask=None):bs = q.size(0)s = q.size(1)# 计算 sin - cos 形式的绝对位置编码 [1, 10, 512] 自动广播 [2, 10, 512]pe = get_positional_encoding(s, self.d_model)pe = pe.unsqueeze(0) # 扩展维度以匹配 x 的形状# PyTorch 支持张量的广播,应用绝对位置编码到 q, k, vq += pek += pev += pe# 进行线性操作划分为成 h 个头k = self.k_linear(k).view(bs, -1, self.h, self.d_k)q = self.q_linear(q).view(bs, -1, self.h, self.d_k)v = self.v_linear(v).view(bs, -1, self.h, self.d_k)# 矩阵转置k = k.transpose(1, 2) # [bs,h,s,d] = [2, 8, 10, 64]q = q.transpose(1, 2)v = v.transpose(1, 2)# 计算 attentionattn = self.attention(q, k, v, self.d_k, mask, self.dropout)# 连接多个头并输入到最后的线性层concat = attn.transpose(1, 2).contiguous().view(bs, -1, self.d_model)output = self.out(concat)return output
def main():# 设置超参数bs, s, h, d = 2, 10, 8, 512dropout_rate = 0.1# 创建 MultiHeadAttention 实例attention = MultiHeadAttention(h, d, dropout_rate)# 创建随机输入张量q = torch.randn(bs, s, d)k = torch.randn(bs, s, d)v = torch.randn(bs, s, d)# 可选:创建掩码,因果掩码,上三角矩阵mask = torch.tril(torch.ones(bs, s, s))# 测试无掩码的情况output_no_mask = attention(q, k, v)print("Output shape without mask:", output_no_mask.shape)# 测试有掩码的情况output_with_mask = attention(q, k, v, mask)print("Output shape with mask:", output_with_mask.shape)# 检查输出是否符合预期assert output_no_mask.shape == (bs, s, d), "Output shape is incorrect without mask"assert output_with_mask.shape == (bs, s, d), "Output shape is incorrect with mask"print("Test passed!")
if __name__ == '__main__':main()
3. 相对位置编码 Relative PE
相对位置编码(Relative Positional Encoding,简称 RPE 或 RePE),在 Transformer-XL 与 T5 中使用相对位置编码,具体的实现方式较多,核心是,相对位置编码的索引矩阵 relative_indices, [ 10 × 10 ] [10 \times 10] [10×10],范围是 [ 0 , 18 ] [0,18] [0,18],一共19个值,即:
[ 9, 8, 7, 6, 5, 4, 3, 2, 1, 0],
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1],
[11, 10, 9, 8, 7, 6, 5, 4, 3, 2],
[12, 11, 10, 9, 8, 7, 6, 5, 4, 3],
[13, 12, 11, 10, 9, 8, 7, 6, 5, 4],
[14, 13, 12, 11, 10, 9, 8, 7, 6, 5],
[15, 14, 13, 12, 11, 10, 9, 8, 7, 6],
[16, 15, 14, 13, 12, 11, 10, 9, 8, 7],
[17, 16, 15, 14, 13, 12, 11, 10, 9, 8],
[18, 17, 16, 15, 14, 13, 12, 11, 10, 9]
索引矩阵的源码:relative_indices = torch.arange(s).unsqueeze(1) - torch.arange(s).unsqueeze(0) + s - 1
参考 Tensor2Tensor 的 common_attention.py 实现方式,注意只是其中一类,即:
A t t e n t i o n ( Q K V ) = S o f t m a x ( Q K ⊤ d m + R e P E i j ) V Attention(QKV) = Softmax(\frac{QK^{\top}}{\sqrt{d_{m}}}+RePE_{ij})V Attention(QKV)=Softmax(dmQK⊤+RePEij)V
即:
import math
import torch
import torch.nn.functional as F
from torch import nn
def relative_positional_encoding(seq_len, dim, theta=10000.0):# 计算位置编码索引,参考 Absolute PE 公式relative_positions = torch.arange(1 - seq_len, seq_len).unsqueeze(1) # [-9,9], 一共19个值# div_term = torch.exp(torch.arange(0, dim, 2) * -(math.log(theta) / dim))div_term = 1.0 / torch.pow(theta, torch.arange(0, dim, 2) / dim)pe = torch.zeros(2 * seq_len - 1, dim)pe[:, 0::2] = torch.sin(relative_positions * div_term)pe[:, 1::2] = torch.cos(relative_positions * div_term)return pe
class MultiHeadAttention(nn.Module):"""多头自注意力机制 MultiHeadAttention"""def __init__(self, heads, d_model, dropout=0.1):super().__init__()self.d_model = d_modelself.d_k = d_model // headsself.h = headsself.q_linear = nn.Linear(d_model, d_model)self.k_linear = nn.Linear(d_model, d_model)self.v_linear = nn.Linear(d_model, d_model)self.out = nn.Linear(d_model, d_model)self.dropout = nn.Dropout(dropout)@staticmethoddef attention(q, k, v, d_k, mask=None, dropout=None):bs, h, s, _ = q.shape# 计算查询和键的注意力分数scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)# ---------- 相对位置编码 RePE ---------- #re_pe = relative_positional_encoding(s, d_k) # [19, 64]# relative_indices 输出 0~18 的方阵 [s,s]re_indices = torch.arange(s).unsqueeze(1) - torch.arange(s).unsqueeze(0) + s - 1 # [10, 10]re = re_pe[re_indices] # [10, 10, 64]# 爱因斯坦公式拆解: q 的维度 [2,8,10,64] -> [10,2,8,64] -> [10,16,64]# re 的维度 [10,10,64], 则 qz' = [10,16,10] -> [10,2,8,10] -> [2,8,10,10]re_scores = torch.einsum('bhrd,rld->bhrl', q, re) # [2, 8, 10, 10]scores = scores + re_scores# ---------- 相对位置编码 RePE ---------- ## 掩盖掉那些为了填补长度增加的单元,使其通过 softmax 计算后为 0if mask is not None:mask = mask.unsqueeze(1)scores = scores.masked_fill(mask == 0, -1e9)scores = F.softmax(scores, dim=-1)if dropout is not None:scores = dropout(scores)output = torch.matmul(scores, v)return outputdef forward(self, q, k, v, mask=None):bs = q.size(0)s = q.size(1)# 进行线性操作划分为成 h 个头k = self.k_linear(k).view(bs, -1, self.h, self.d_k)q = self.q_linear(q).view(bs, -1, self.h, self.d_k)v = self.v_linear(v).view(bs, -1, self.h, self.d_k)# 矩阵转置k = k.transpose(1, 2) # [bs,h,s,d] = [2, 8, 10, 64]q = q.transpose(1, 2)v = v.transpose(1, 2)# 计算注意力attn = self.attention(q, k, v, self.d_k, mask, self.dropout)# 连接多个头并输入到最后的线性层concat = attn.transpose(1, 2).contiguous().view(bs, -1, self.d_model)output = self.out(concat)return output
def main():# 设置超参数bs, s, h, d = 2, 10, 8, 512dropout_rate = 0.1# 创建 MultiHeadAttention 实例attention = MultiHeadAttention(h, d, dropout_rate)# 创建随机输入张量q = torch.randn(bs, s, d)k = torch.randn(bs, s, d)v = torch.randn(bs, s, d)# 可选:创建掩码,因果掩码,上三角矩阵mask = torch.tril(torch.ones(bs, s, s))# 测试无掩码的情况output_no_mask = attention(q, k, v)print("Output shape without mask:", output_no_mask.shape)# 测试有掩码的情况output_with_mask = attention(q, k, v, mask)print("Output shape with mask:", output_with_mask.shape)# 检查输出是否符合预期assert output_no_mask.shape == (bs, s, d), "Output shape is incorrect without mask"assert output_with_mask.shape == (bs, s, d), "Output shape is incorrect with mask"print("Test passed!")
if __name__ == '__main__':main()
相关文章:

LeetCode - Google 大模型10题 第2天 Position Embedding(位置编码) 3题
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/145454489 在 Transformer 架构中,位置编码(Position Embedding) 是辅助模型理解序列中元素顺序的关键机制。绝对位置编码(Absolute P…...

PostgreSQL 数据库备份与还原
为了安全与数据共享等,创建好的数据库有时候需要备份操作和还原操作。数据库的备份与还原主要是三个命令:pg_dump、pg_dumpall 和 pg_restore 。 其中pg_dump用于备份单个数据库,它支持多种备份格式(SQL、自定义等)&a…...

proxmox通过更多的方式创建虚拟机
概述 作为一名资深运维工程师,我们经常需要在 Proxmox 虚拟化平台上创建和管理虚拟机。本文将介绍三种不同的方式在 Proxmox 上创建 Ubuntu 虚拟机: 通过 Proxmox 命令创建虚拟机通过 Shell 脚本自动化创建虚拟机使用 Proxmox API 创建虚拟机 每种方式…...
WordPress使用(2)
上一篇文章讲述了WordPress的基本安装,主要是docker方式的处理。本文章主要介绍WordPress安装后的其他设置。 1. 安装后设置 安装后碰到的第一个需求就是安装一个合适的主题,但WordPress默认的上传文件大小是2M,远远无法满足要求࿰…...

git中文件的状态状态切换
文件的状态分类 Git 中文件的状态主要分为以下几种: Untracked(未跟踪) 定义:这些文件从未被 Git 跟踪过,通常是因为它们是新创建的文件,或者被 .gitignore 排除在外。 示例:新创建的文件 new…...

解决php8.3无法加载curl扩展
把它的值更改为扩展存在的目录的绝对路径(扩展存在的目录为有php_xxx.dll存在的目录) extension_dir "e:\serv\php83\ext" 然后从php根目录复制 libssh2.dll 和 libcrypto-*.dll 和 libssl-*.dll 到Apache根目录下的bin目录 重启apache服务即可...

三路排序算法
三路排序算法 引言 排序算法是计算机科学中基础且重要的算法之一。在数据分析和处理中,排序算法的效率直接影响着程序的执行速度和系统的稳定性。本文将深入探讨三路排序算法,包括其原理、实现和应用场景。 一、三路排序算法的原理 三路排序算法是一…...

入行FPGA设计工程师需要提前学习哪些内容?
FPGA作为一种灵活可编程的硬件平台,广泛应用于嵌入式系统、通信、数据处理等领域。很多人选择转行FPGA设计工程师,但对于新手来说,可能在学习过程中会遇到一些迷茫和困惑。为了帮助大家更好地准备,本文将详细介绍入行FPGA设计工程…...

DBASE DBF数据库文件解析
基于Java实现DBase DBF文件的解析和显示 JDK19编译运行,实现了数据库字段和数据解析显示。 首先解析数据库文件头代码 byte bytes[] Files.readAllBytes(Paths.get(file));BinaryBufferArray bis new BinaryBufferArray(bytes);DBF dbf new DBF();dbf.VersionN…...

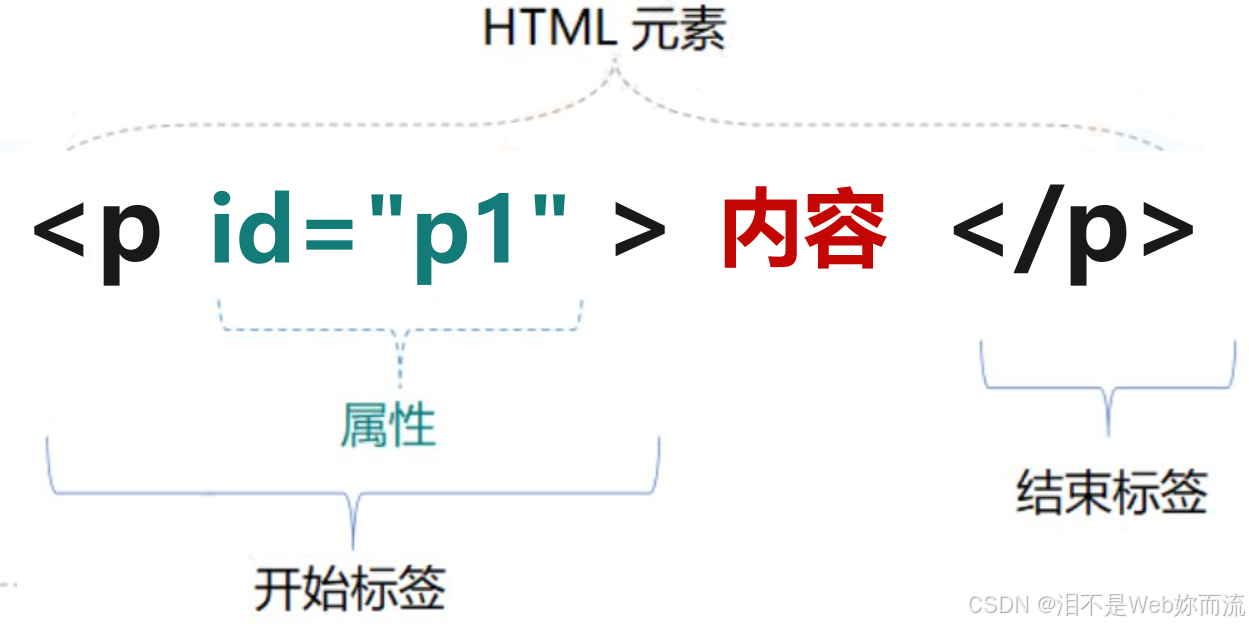
html基本结构和常见元素
html5文档基本结构 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>文档标题</title> </head> <body>文档正文部分 </body> </html> html文档可分为文档头和文档体…...

JAVAweb学习日记(十) Mybatis入门操作
一、介绍 二、快速入门程序 三、入门-数据库连接池 四、入门-lombok工具包...

从Transformer到世界模型:AGI核心架构演进
文章目录 引言:架构革命推动AGI进化一、Transformer:重新定义序列建模1.1 注意力机制的革命性突破1.2 从NLP到跨模态演进1.3 规模扩展的黄金定律 二、通向世界模型的关键跃迁2.1 从语言模型到认知架构2.2 世界模型的核心特征2.3 混合架构的突破 三、构建…...

Rk3588芯片介绍(含数据手册)
芯片介绍:RK3588是一款低功耗,高性能的处理器,适用于基于arm的PC和边缘计算设备,个人移动互联网设备和其他数字多媒体应用,集成了四核Cortex-A76和四核Cortex-A55以及单独的NEON协处理器 视频处理方面:提供…...

java开发面试自我介绍模板_java面试自我介绍3篇
java 面试自我介绍 3 篇 java 面试自我介绍篇一: 我叫赵,我的同学更都喜欢称呼我的英文名字,叫,六月的 意思,是君的谐音。我来自安徽的市,在 21 年我以市全市第一名 的成绩考上了大学,…...

w193基于Spring Boot的秒杀系统设计与实现
🙊作者简介:多年一线开发工作经验,原创团队,分享技术代码帮助学生学习,独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取,记得注明来意哦~🌹赠送计算机毕业设计600个选题excel文…...

chrome浏览器chromedriver下载
chromedriver 下载地址 https://googlechromelabs.github.io/chrome-for-testing/ 上面的链接有和当前发布的chrome浏览器版本相近的chromedriver 实际使用感受 chrome浏览器会自动更新,可以去下载最新的chromedriver使用,自动化中使用新的chromedr…...
【HTML入门】Sublime Text 4与 Phpstorm
文章目录 前言一、环境基础1.Sublime Text 42.Phpstorm(1)安装(2)启动Phpstorm(3)“启动”码 二、HTML1.HTML简介(1)什么是HTML(2)HTML版本及历史(3)HTML基本结构 2.HTML简单语法(1)HTML标签语法(2)HTML常用标签(3)表格(4)特殊字符 总结 前言 在当今的软件开发领域,…...

Python----Python高级(并发编程:进程Process,多进程,进程间通信,进程同步,进程池)
一、进程Process 拥有自己独立的堆和栈,既不共享堆,也不共享栈,进程由操作系统调度;进程切换需要的资源很最大,效率低。 对于操作系统来说,一个任务就是一个进程(Process)ÿ…...

汽车自动驾驶AI
汽车自动驾驶AI是当前汽车技术领域的前沿方向,以下是关于汽车自动驾驶AI的详细介绍: 技术原理 感知系统:自动驾驶汽车通过多种传感器(如激光雷达、摄像头、雷达、超声波传感器等)收集周围环境的信息。AI算法对这些传感…...

Linux之安装MySQL
1、查看系统当前版本是多少位的 getconf LONG_BIT2.去官网下载对应的MYSQL安装包 这里下载的是8版本的,位数对应之前的64位 官网地址:https://downloads.mysql.com/archives/community/ 3.上传压缩包 4.到对应目录下解压 tar -xvf mysql-8.0.26-lin…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
