当前位置：首页 > news >正文

RK3568使用QT搭建TCP服务器和客户端

news 2026/2/9 5:05:39

文章目录

一、让RK3568开发板先连接上wifi
二、客户端代码
- - 1. `widget.h` 文件
  - 2. `widget.cpp` 文件
  - **详细讲解**
  - - 1. **`Widget` 类构造函数 (`Widget::Widget`)**
    - 2. **UI 布局 (`setupUI`)**
    - 3. **连接按钮的槽函数 (`onConnectClicked`)**
    - 4. **发送消息按钮的槽函数 (`onSendMessageClicked`)**
    - 5. **接收数据的槽函数 (`onDataReceived`)**
  - 总结
三、服务器代码
- - `widget.h` (服务器端头文件)
  - `widget.cpp` (服务器端实现)
  - **详细讲解**
  - - 1. **`Widget` 类构造函数 (`Widget::Widget`)**
    - 2. **UI 布局 (`setupUI`)**
    - 3. **启动服务器 (`onStartServerClicked`)**
    - 4. **处理新的客户端连接 (`onNewConnection`)**
    - 5. **发送消息到客户端 (`onSendMessageClicked`)**
    - 6. **接收客户端数据 (`onDataReceived`)**
  - 总结

一、让RK3568开发板先连接上wifi

在这里插入图片描述
测试是否可以ping通百度：

在这里插入图片描述

二、客户端代码

1. `widget.h` 文件

#ifndef WIDGET_H
#define

RK3568使用QT搭建TCP服务器和客户端

文章目录一、让RK3568开发板先连接上wifi二、客户端代码1. `widget.h` 文件2. `widget.cpp` 文件**详细讲解**1. **`Widget` 类构造函数 (`Widget::Widget`)**2. **UI 布局 (`setupUI`)**3. **连接按钮的槽函数 (`onConnectClicked`)**4. **发送消息按钮的槽函数 (`onSendMess…...

编程日记 2025/2/6 22:09:20

Android学习20 -- 手搓App2（Gradle）

1 前言昨天写了一个完全手搓的：Android学习19 -- 手搓App-CSDN博客后面谷歌说不要用aapt，d8这些来搞。其实不想弄Gradle的，不过想着既然开始了，就多看一些。之前写过一篇Gradle，不过是最简单的编译，不涉…...

编程日记 2025/2/6 22:08:20

LeetCode - Google 大模型10题第2天 Position Embedding(位置编码) 3题

欢迎关注我的CSDN：https://spike.blog.csdn.net/ 本文地址：https://spike.blog.csdn.net/article/details/145454489 在 Transformer 架构中，位置编码(Position Embedding) 是辅助模型理解序列中元素顺序的关键机制。绝对位置编码(Absolute P…...

编程日记 2025/2/6 22:01:10

PostgreSQL 数据库备份与还原

为了安全与数据共享等，创建好的数据库有时候需要备份操作和还原操作。数据库的备份与还原主要是三个命令：pg_dump、pg_dumpall 和 pg_restore 。其中pg_dump用于备份单个数据库，它支持多种备份格式（SQL、自定义等）&a…...

编程日记 2025/2/6 22:00:09

proxmox通过更多的方式创建虚拟机

概述作为一名资深运维工程师，我们经常需要在 Proxmox 虚拟化平台上创建和管理虚拟机。本文将介绍三种不同的方式在 Proxmox 上创建 Ubuntu 虚拟机： 通过 Proxmox 命令创建虚拟机通过 Shell 脚本自动化创建虚拟机使用 Proxmox API 创建虚拟机每种方式…...

编程日记 2025/2/6 21:58:06

WordPress使用（2）

上一篇文章讲述了WordPress的基本安装，主要是docker方式的处理。本文章主要介绍WordPress安装后的其他设置。 1. 安装后设置安装后碰到的第一个需求就是安装一个合适的主题，但WordPress默认的上传文件大小是2M，远远无法满足要求&#xff0…...

编程日记 2025/2/6 21:52:59

git中文件的状态状态切换

文件的状态分类 Git 中文件的状态主要分为以下几种： Untracked（未跟踪） 定义：这些文件从未被 Git 跟踪过，通常是因为它们是新创建的文件，或者被 .gitignore 排除在外。示例：新创建的文件 new…...

编程日记 2025/2/6 21:50:57

解决php8.3无法加载curl扩展

把它的值更改为扩展存在的目录的绝对路径(扩展存在的目录为有php_xxx.dll存在的目录) extension_dir "e:\serv\php83\ext" 然后从php根目录复制 libssh2.dll 和 libcrypto-*.dll 和 libssl-*.dll 到Apache根目录下的bin目录重启apache服务即可...

编程日记 2025/2/6 21:48:55

三路排序算法

三路排序算法引言排序算法是计算机科学中基础且重要的算法之一。在数据分析和处理中，排序算法的效率直接影响着程序的执行速度和系统的稳定性。本文将深入探讨三路排序算法，包括其原理、实现和应用场景。一、三路排序算法的原理三路排序算法是一…...

编程日记 2025/2/6 21:34:41

入行FPGA设计工程师需要提前学习哪些内容？

FPGA作为一种灵活可编程的硬件平台，广泛应用于嵌入式系统、通信、数据处理等领域。很多人选择转行FPGA设计工程师，但对于新手来说，可能在学习过程中会遇到一些迷茫和困惑。为了帮助大家更好地准备，本文将详细介绍入行FPGA设计工程…...

编程日记 2025/2/6 21:30:37

DBASE DBF数据库文件解析

基于Java实现DBase DBF文件的解析和显示 JDK19编译运行，实现了数据库字段和数据解析显示。首先解析数据库文件头代码 byte bytes[] Files.readAllBytes(Paths.get(file));BinaryBufferArray bis new BinaryBufferArray(bytes);DBF dbf new DBF();dbf.VersionN…...

编程日记 2025/2/6 21:29:35

html基本结构和常见元素

html5文档基本结构 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>文档标题</title> </head> <body>文档正文部分 </body> </html> html文档可分为文档头和文档体…...

编程日记 2025/2/6 21:16:20

JAVAweb学习日记（十） Mybatis入门操作

一、介绍二、快速入门程序三、入门-数据库连接池四、入门-lombok工具包...

编程日记 2025/2/6 21:14:18

从Transformer到世界模型：AGI核心架构演进

文章目录引言：架构革命推动AGI进化一、Transformer：重新定义序列建模1.1 注意力机制的革命性突破1.2 从NLP到跨模态演进1.3 规模扩展的黄金定律二、通向世界模型的关键跃迁2.1 从语言模型到认知架构2.2 世界模型的核心特征2.3 混合架构的突破三、构建…...

编程日记 2025/2/6 21:12:12

Rk3588芯片介绍（含数据手册）

芯片介绍：RK3588是一款低功耗，高性能的处理器，适用于基于arm的PC和边缘计算设备，个人移动互联网设备和其他数字多媒体应用，集成了四核Cortex-A76和四核Cortex-A55以及单独的NEON协处理器视频处理方面：提供…...

编程日记 2025/2/6 21:07:08

java开发面试自我介绍模板_java面试自我介绍3篇

java 面试自我介绍 3 篇 java 面试自我介绍篇一： 我叫赵，我的同学更都喜欢称呼我的英文名字，叫，六月的意思，是君的谐音。我来自安徽的市，在 21 年我以市全市第一名的成绩考上了大学&#xff0c…...

编程日记 2025/2/6 21:06:07

w193基于Spring Boot的秒杀系统设计与实现

🙊作者简介：多年一线开发工作经验，原创团队，分享技术代码帮助学生学习，独立完成自己的网站项目。代码可以查看文章末尾⬇️联系方式获取，记得注明来意哦~🌹赠送计算机毕业设计600个选题excel文…...

编程日记 2025/2/6 21:01:00

chrome浏览器chromedriver下载

chromedriver 下载地址 https://googlechromelabs.github.io/chrome-for-testing/ 上面的链接有和当前发布的chrome浏览器版本相近的chromedriver 实际使用感受 chrome浏览器会自动更新，可以去下载最新的chromedriver使用，自动化中使用新的chromedr…...

编程日记 2025/2/6 20:59:59

【HTML入门】Sublime Text 4与 Phpstorm

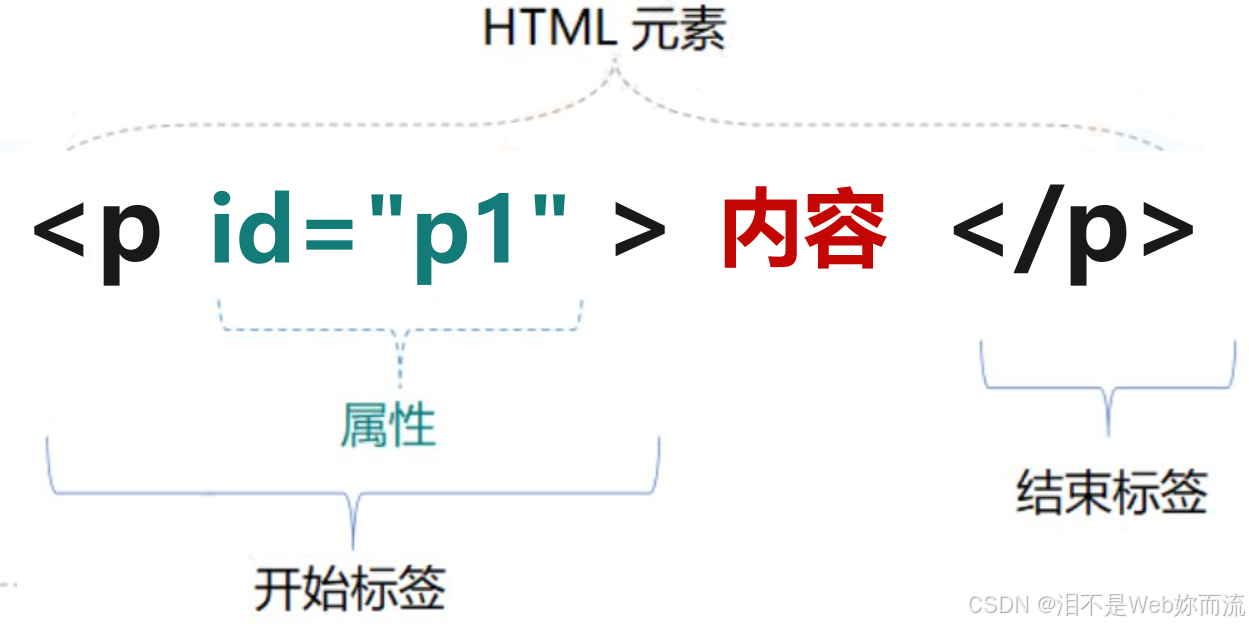
文章目录前言一、环境基础1.Sublime Text 42.Phpstorm(1)安装(2)启动Phpstorm(3)“启动”码二、HTML1.HTML简介(1)什么是HTML(2)HTML版本及历史(3)HTML基本结构 2.HTML简单语法(1)HTML标签语法(2)HTML常用标签(3)表格(4)特殊字符总结前言在当今的软件开发领域&#xff0c…...

编程日记 2025/2/6 20:56:56

Python----Python高级（并发编程：进程Process，多进程，进程间通信，进程同步，进程池）

一、进程Process 拥有自己独立的堆和栈，既不共享堆，也不共享栈，进程由操作系统调度；进程切换需要的资源很最大，效率低。对于操作系统来说，一个任务就是一个进程（Process）&#xff…...

编程日记 2025/2/6 20:54:51

【kafka】Golang实现分布式Masscan任务调度系统

要求： 输出两个程序，一个命令行程序（命令行参数用flag）和一个服务端程序。命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽，然后将消息推送到kafka里面。服务端程序： 从kafka消费者接收…...

编程新知 2026/2/8 20:41:58

Rust 异步编程

Rust 异步编程引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。异步编程基础什么是异步…...

编程新知 2025/11/17 18:58:56

Swagger和OpenApi的前世今生

Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章，二者共同塑造了现代RESTful API的开发范式。本期就扒一扒其技术演进的关键节点与核心逻辑： 🔄 一、起源与初创期：Swagger的诞生（2010-2014） 核心…...

编程新知 2026/1/25 9:08:41

算法岗面试经验分享-大模型篇

文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer （1）资源论文&a…...

编程新知 2026/1/23 11:58:06