图论常见算法
图论常见算法
- 算法
- prim算法
- Dijkstra算法
- 用途
- 最小生成树(MST):
- 最短路径:
- 拓扑排序:
- 关键路径:
| 算法 | 用途 | 适用条件 | 时间复杂度 |
|---|---|---|---|
| Kruskal | 最小生成树 | 无向图(稀疏图) | O(E log E) |
| Prim | 最小生成树 | 无向图(稠密图) | O(V^2) 或 O(E log V) |
| Dijkstra | 单源最短路径 | 非负权图 | O(V^2) 或 O(E + V log V) |
| Floyd | 多源最短路径 | 允许负权边(无负权环) | O(V^3) |
| AOV | 拓扑排序 | 有向无环图(DAG) | O(V + E) |
| AOE | 关键路径 | 有向无环图(DAG) | O(V + E) |
算法
prim算法

key[MAXN]:存储从MST到每个顶点的最小权重(边)。
inMST[MAXN]:标记每个顶点是否已经在MST中。
优先队列:使用priority_queue(最小堆)来选择当前最小权重边对应的顶点。
-
初始化:
选择一个起始顶点,将其加入生成树。
初始化一个优先队列(最小堆),用于存储所有连接生成树和非生成树顶点的边,按权重排序。
初始化一个数组key,记录每个顶点到生成树的最小权重,起始顶点为0,其余顶点为无穷大(表示未连接)。
初始化一个数组inMST,用于标记每个节点是否已经加入MST中。 -
迭代过程
从优先队列中取出权重最小的边,将其对应的顶点u加入生成树。
遍历u的所有邻接顶点v:如果v未被加入生成树,且边(u, v)的权重小于key[v],则更新key[v]为(u, v)的权重,并将v加入优先队列。
typedef pair<int, int> pii; // 用于表示 (权重, 节点)
const int INF = INT_MAX;void prim(int n, vector<vector<pii>>& adj) {vector<int> key(n, INF); // 存储到每个节点的最小边权vector<bool> inMST(n, false); // 标记节点是否在生成树中priority_queue<pii, vector<pii>, greater<pii>> pq; // 最小堆,存储 (边权, 节点)key[0] = 0; // 从节点 0 开始pq.push({0, 0}); // 初始时将起点加入堆while (!pq.empty()) {int u = pq.top().second; // 当前节点pq.pop();if (inMST[u]) continue; // 如果已经在生成树中,跳过inMST[u] = true; // 标记为在生成树中// 遍历 u 的邻接节点for (auto& edge : adj[u]) {int v = edge.first;int weight = edge.second;// 如果节点 v 不在生成树中且通过 u 到 v 的边更短if (!inMST[v] && weight < key[v]) {key[v] = weight;pq.push({key[v], v}); // 更新最小堆}}}
}
Dijkstra算法

dis[MAXN]:存储从起点到每个节点的最短距离。
vis[MAXN]:标记每个节点是否已被访问。
优先队列:使用priority_queue(最小堆)来选择最短距离对应的顶点。
-
初始化:
选择一个起点。
初始化一个优先队列,用于存储到起点的距离。
初始化一个数组dis,用于存储从起点到每个节点的最短距离。起始顶点为0,其余顶点为无穷大(表示未连接)。
初始化一个数组vis,用于标记每个节点是否已经被访问过(即是否已经找到从起点到该节点的最短路径)。 -
迭代过程
从优先队列中取出离起点的最短距离对应的顶点u。
遍历u的所有邻接顶点v:如果v未被访问,且(u, v)的距离小于dis[v],则更新dis[v]为(u, v)的距离,并将v加入优先队列。
struct edge {int v, w;
};struct node {int dis, u;bool operator>(const node& a) const { return dis > a.dis; }
};vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
priority_queue<node, vector<node>, greater<node>> q;void dijkstra(int n, int s) {memset(dis, 0x3f, (n + 1) * sizeof(int));memset(vis, 0, (n + 1) * sizeof(int));dis[s] = 0;q.push({0, s});while (!q.empty()) {int u = q.top().u;q.pop();if (vis[u]) continue;vis[u] = 1;// BFSfor (auto ed : e[u]) {int v = ed.v, w = ed.w;if (dis[v] > dis[u] + w) {dis[v] = dis[u] + w;q.push({dis[v], v});}}}
}
用途
最小生成树(MST):
用途:最小生成树用于找到一个连通图中所有节点的最小连接总成本的树。它被广泛应用于网络设计、构建最优电路、电力网络、交通规划等领域。
实际应用:如设计最小成本的通讯网络、城市间的最短道路规划等。
最短路径:
用途:最短路径算法用于寻找图中两个节点之间的最短路径。它广泛应用于导航系统、网络路由、物流调度等。
实际应用:如计算地图上的最短路线、在网络中寻找数据传输的最优路径等。
拓扑排序:
用途:拓扑排序是有向无环图(DAG)的一种排序方式,确保每个节点都在它依赖的节点之前。它通常用于任务调度、编译器优化、项目计划等。
实际应用:如任务调度中的优先级排序、编译过程中的模块依赖关系等。
关键路径:
用途:关键路径方法(CPM)用于项目管理中,帮助确定哪些任务是“关键”的,即那些对项目完成时间有直接影响的任务。它能帮助管理者合理安排资源,避免延误。
实际应用:如建筑工程的项目管理、软件开发的进度控制等。
相关文章:

图论常见算法
图论常见算法 算法prim算法Dijkstra算法 用途最小生成树(MST):最短路径:拓扑排序:关键路径: 算法用途适用条件时间复杂度Kruskal最小生成树无向图(稀疏图)O(E log E)Prim最小生成树无…...

MySQL三大日志详解
在MySQL数据库的运行过程中,三大关键日志——binlog、redo log和undo log,起着至关重要的作用。理解这三大日志,对于深入掌握MySQL的工作原理、数据恢复以及主从复制等操作有着极大的帮助。本文将详细剖析这三大日志的作用和工作机制。 Binl…...

【SQL 中的分组查询与联合查询详解】
文章目录 SQL 中的分组查询与联合查询详解 1. GROUP BY分组查询 1.1 语句格式1.2 示例说明 1.2.1 分别查询哥哥组和弟弟组的英语成绩总和1.2.2 查询哥哥组的所有成绩总和 2. 联合查询 2.1 内连接 2.1.1 语法格式2.1.2 执行过程 2.2 外连接 2.2.1 左外连接2.2.2 右外连接 2.3 …...

【实战篇】用 Cursor 独立开发并上线电商类 Android APP 全攻略
一、为啥要用 Cursor 开发电商类 Android APP 家人们,如今电商类 APP 随处可见,不管是买衣服、食品,还是电子产品,都能通过这些 APP 轻松搞定。要是能自己开发一款电商类 Android APP,那可太酷啦!但开发 APP 可不是一件容易的事,涉及到很多技术,像写代码、设计界面、处…...

quartus24.1版本子模块因时钟问题无法综合通过,FPGA过OOC问题复盘
因为只负责一个子模块,所以需要单独对该子模块进行综合和过OOC,这时候已经有一些加虚拟pin文件,敲命令让子模块能过OOC的方法。但这个方法的前提是先过综合,然后再敲命令让虚拟管脚命令成功,最终可以过OOC。 今天负责…...

零基础Vue入门6——Vue router
本节重点: 路由定义路由跳转 前面几节学习的都是单页面的功能(都在专栏里面https://blog.csdn.net/zhanggongzichu/category_12883540.html),涉及到项目研发都是有很多页面的,这里就需要用到路由(vue route…...

使用 Let‘s Encrypt 和 OpenResty 实现域名转发与 SSL 配置
在搭建网站或服务时,确保域名的安全性和正确的流量转发是非常重要的。本文将介绍如何使用 Let’s Encrypt 获取免费的 SSL 证书,并将其配置到 OpenResty 中,同时实现特定的域名转发规则。这不仅可以提升网站的安全性,还能优化流量…...

Lambda 表达式
一、Lambda 表达式简介 Lambda 表达式是一种简洁的函数式编程方式,用于实现只有一个方法的接口(例如函数式接口)。 基本语法 (parameters) -> expression (parameters) -> { statements; } 参数:可以有零个或多个参数。…...

TCN时间卷积神经网络多变量多步光伏功率预测(Matlab)
代码下载:TCN时间卷积神经网络多变量多步光伏功率预测(Matlab) TCN时间卷积神经网络多变量多步光伏功率预测 一、引言 1.1、研究背景和意义 随着全球能源危机的加剧和环保意识的提升,可再生能源,尤其是太阳能&…...

【Elasticsearch】 Composite Aggregation 详解
1.什么是 Composite Aggregation? Composite Aggregation 是 Elasticsearch 中的一种特殊聚合方式,适用于需要分页展示的聚合结果。它与传统的聚合方式不同,采用了基于游标的分页模型。这种聚合方式可以高效地处理多级聚合中的所有桶&#x…...

如何通过 Logstash 将数据采集到 Elasticsearch
作者:来自 Elastic Andre Luiz 将 Logstash 与 Elasticsearch 集成以实现高效的数据提取、索引和搜索的分步指南。 什么是 Logstash? Logstash 是一种广泛使用的 Elastic Stack 工具,用于实时处理大量日志数据。它充当高效的数据管道&#x…...

mysql的cpu使用率100%问题排查
背景 线上mysql服务器经常性出现cpu使用率100%的告警, 因此整理一下排查该问题的常规流程。 1. 确认CPU占用来源 检查系统进程 使用 top 或 htop 命令,确认是否是 mysqld 进程导致CPU满载:top -c -p $(pgrep mysqld)2. 实时分析MySQL活动 …...

centos虚拟机迁移没有ip的问题
故事背景,我们的centos虚拟机本来是好好的,但是拷贝到其他电脑上就不能分配ip,我个人觉得这个vmware他们软件应该搞定这个啊,因为这个问题是每次都会出现的。 网络选桥接 网络启动失败 service network restart Restarting netw…...

接入 deepseek 实现AI智能问诊
1. 准备工作 注册 DeepSeek 账号 前往 DeepSeek 官网 注册账号并获取 API Key。 创建 UniApp 项目 使用 HBuilderX 创建一个新的 UniApp 项目(选择 Vue3 或 Vue2 模板)。 安装依赖 如果需要在 UniApp 中使用 HTTP 请求,推荐使用 uni.requ…...

用AVFrame + AVPacket 完成accede编码和直接用ffmpeg命令行实现acc编码的对比
在使用 FFmpeg 进行 AAC 音频编码时,可以选择两种方式:通过编程接口(如 AVFrame 和 AVPacket)实现 AAC 编码,或者直接使用 FFmpeg 命令行工具。这两种方式各有特点,适用于不同的场景。以下是对两种方法的详细分析,包括它们的区别、优缺点以及适用场景。 一、通过 AVFram…...

计算机网络笔记再战——理解几个经典的协议6——TCP与UDP
目录 先说端口号 TCP 使用序号保证顺序性和应答来保证有效性 超时重传机制 TCP窗口机制 UDP 路由协议 协议分类:IGP和EGP 几个经典的路由算法 RIP OSPF 链路状态数据库(LSDB) LSA(Link State Advertisement࿰…...
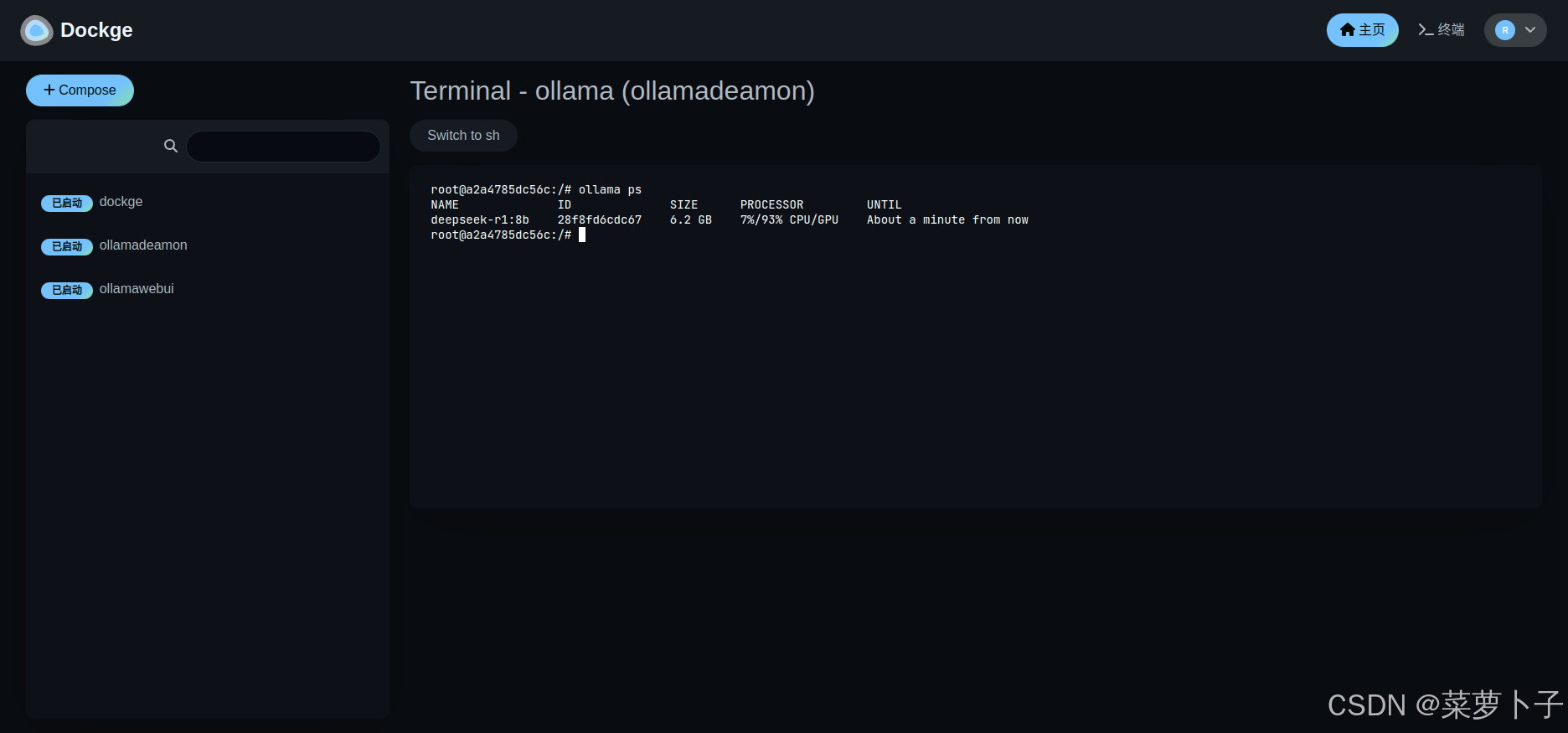
【AI】在Ubuntu中使用docker对DeepSeek的部署与使用
这篇文章前言是我基于部署好的deepseek-r1:8b模型跑出来的 关于部署DeepSeek的前言与介绍 在当今快速发展的技术环境中,有效地利用机器学习工具来解决问题变得越来越重要。今天,我将引入一个名为DeepSeek 的工具,它作为一种强大的搜索引擎&a…...

openssl使用
openssl使用 提取密钥对 数字证书pfx包含公钥和私钥,而cer证书只包含公钥。提取需输入证书保护密码 openssl pkcs12 -in xxx.pfx -nocerts -nodes -out pare.key提取私钥 openssl rsa -in pare.key -out pri.key提取公钥 openssl rsa -in pare.key -pubout -ou…...

《语义捕捉全解析:从“我爱自然语言处理”到嵌入向量的全过程》
首先讲在前面,介绍一些背景 RAG(Retrieval-Augmented Generation,检索增强生成) 是一种结合了信息检索与语言生成模型的技术,通过从外部知识库中检索相关信息,并将其作为提示输入给大型语言模型ÿ…...

HIVE如何注册UDF函数
如果注册UDF函数的时候报了上面的错误,说明hdfs上传的路径不正确, 一定要用下面的命令 hadoop fs -put /tmp/hive/111.jar /user/hive/warehouse 一定要上传到上面路径,这样在创建函数时,引用下面的地址就可以创建成功...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
