6.Centos7上部署flask+SQLAlchemy+python+达梦数据库
情况说明
前面已经介绍了window上使用pycharm工具开发项目时,window版的python连接达梦数据库需要的第三方包。
这篇文章讲述,centos7上的python版本连接达梦数据库需要的第三方包。
之前是在windows上安装达梦数据库的客户端,将驱动包安装到windows版本的python中。(开发人员本地开发需要)
现在是在linux上安装达梦数据库的客户端,将驱动包安装到Centos7版本的python中。(实际项目部署需要)
达梦数据库服务端依然是通过docker部署在Centos7服务器上的。
先查看linux系统的基本信息
#获取系统位数 getconf LONG_BIT
#查询操作系统release信息 lsb_release -a
#查询系统信息 cat /etc/issue
#查询系统名称 uname -a
![]()
到官网下载与系统匹配的软件

下载后解
相关文章:

6.Centos7上部署flask+SQLAlchemy+python+达梦数据库
情况说明 前面已经介绍了window上使用pycharm工具开发项目时,window版的python连接达梦数据库需要的第三方包。 这篇文章讲述,centos7上的python版本连接达梦数据库需要的第三方包。 之前是在windows上安装达梦数据库的客户端,将驱动包安装到windows版本的python中。(开…...

【C语言系列】深入理解指针(5)
深入理解指针(5) 一、sizeof和strlen的对比1.1sizeof1.2strlen1.3sizeof和strlen的对比 二、数组和指针笔试题解析2.1 一维数组2.2 字符数组2.2.1代码1:2.2.2代码2:2.2.3代码3:2.2.4代码4:2.2.5代码5&#…...

mysql自连接 处理层次结构数据
MySQL 的自连接(Self Join)是一种特殊的连接方式,它允许一个表与自身进行连接。自连接通常用于处理具有层次结构或递归关系的数据,或者当同一张表中的数据需要相互关联时。以下是几种常见的场景,说明何时应该使用自连接…...

##__VA_ARGS__有什么作用
##__VA_ARGS__ 是 C/C 中宏定义(Macro)的一种特殊用法,主要用于可变参数宏(Variadic Macros)的场景,解决当可变参数为空时可能导致的语法错误问题。以下是详细解释: 核心作用 消除空参数时的多余…...
返回不到上个页面)
鸿蒙 router.back()返回不到上个页面
1. 检查页面栈(Page Stack) 鸿蒙的路由基于页面栈管理,确保上一个页面存在且未被销毁。 使用 router.getLength() 检查当前页面栈长度: console.log(当前页面栈长度: ${router.getLength()}); 如果结果为 1,说明没有上…...

深度学习模型蒸馏技术的发展与应用
随着人工智能技术的快速发展,大型语言模型和深度学习模型在各个领域展现出惊人的能力。然而,这些模型的规模和复杂度也带来了显著的部署挑战。模型蒸馏技术作为一种优化解决方案,正在成为连接学术研究和产业应用的重要桥梁。本文将深入探讨模…...

STM32G0B1 ADC DMA normal
目标 ADC 5个通道,希望每1秒采集一遍; CUBEMX 配置 添加代码 #define ADC1_CHANNEL_CNT 5 //采样通道数 #define ADC1_CHANNEL_FRE 3 //单个通道采样次数,用来取平均值 uint16_t adc1_val_buf[ADC1_CHANNEL_CNT*ADC1_CHANNEL_FRE]; //传递…...

<tauri><rust><GUI>基于rust和tauri,在已有的前端框架上手动集成tauri示例
前言 本文是基于rust和tauri,由于tauri是前、后端结合的GUI框架,既可以直接生成包含前端代码的文件,也可以在已有的前端项目上集成tauri框架,将前端页面化为桌面GUI。 环境配置 系统:windows 10 平台:visu…...
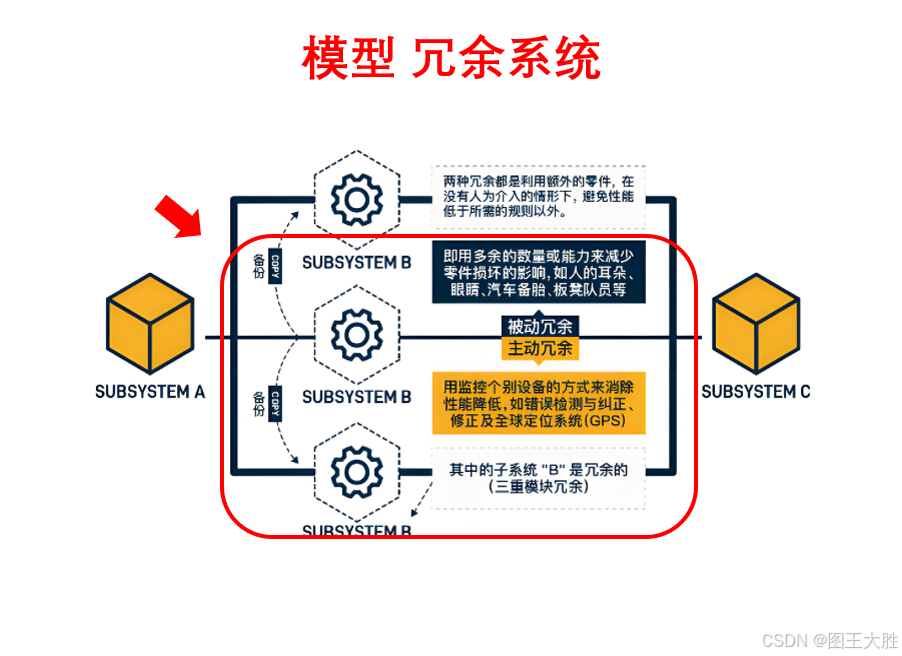
模型 冗余系统(系统科学)
系列文章分享模型,了解更多👉 模型_思维模型目录。为防故障、保运行的备份机制。 1 冗余系统的应用 1.1 冗余系统在企业管理中的应用-金融行业信息安全的二倍冗余技术 在金融行业,信息安全是保障业务连续性和客户资产安全的关键。随着数字化…...

Deepseek部署的模型参数要求
DeepSeek 模型部署硬件要求 模型名称参数量显存需求(推理)显存需求(微调)CPU 配置内存要求硬盘空间适用场景DeepSeek-R1-1.5B1.5B4GB8GB最低 4 核(推荐多核)8GB3GB低资源设备部署,如树莓派、旧…...

AI-学习路线图-PyTorch-我是土堆
1 需求 PyTorch深度学习快速入门教程(绝对通俗易懂!)【小土堆】_哔哩哔哩_bilibili PyTorch 深度学习快速入门教程 配套资源 链接 视频教程 https://www.bilibili.com/video/BV1hE411t7RN/ 文字教程 https://blog.csdn.net/xiaotudui…...

[LeetCode]day17 349.两个数组的交集
https://leetcode.cn/problems/intersection-of-two-arrays/description/ 题目描述 给定两个数组 nums1 和 nums2 ,返回它们的交集。 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序 。 示例 1: 输入:nums1 [1,2,2,1…...

axios 发起 post请求 json 需要传入数据格式
• 1. axios 发起 post请求 json 传入数据格式 • 2. axios get请求 1. axios 发起 post请求 json 传入数据格式 使用 axios 发起 POST 请求并以 JSON 格式传递数据是前端开发中常见的操作。 下面是一个简单的示例,展示如何使用 axios 向服务器发送包含 JSON 数…...

linux交叉编译paho-mqtt-c
下载源代码: https://github.com/eclipse-paho/paho.mqtt.c.git 编译: 如果mqtt不需要SSL安全认证,可以直接执行(注意把编译工具链路径改成自己的) cd paho.mqtt.c-1.3.13/ mkdir install # 创建安装目录 mkdir…...
)
feign Api接口中注解问题:not annotated with HTTP method type (ex. GET, POST)
Bug Description 在调用Feign api时,出现如下异常: java.lang.IllegalStateException: Method PayFeignSentinelApi#getPayByOrderNo(String) not annotated with HTTPReproduciton Steps 1.启动nacos-pay-provider服务,并启动nacos-pay-c…...

安装指定版本的pnpm
要安装指定版本的 pnpm,可以使用以下方法: 方法 1: 使用 pnpm 安装指定版本 你可以通过 pnpm 的 add 命令来安装指定版本: pnpm add -g pnpm<版本号>例如,安装 pnpm 的 7.0.0 版本: pnpm add -g pnpm7.0.0方法…...

【系统设计】Spring、SpringMVC 与 Spring Boot 技术选型指南:人群、场景与实战建议
在 Java 开发领域,Spring 生态的技术选型直接影响项目的开发效率、维护成本和长期扩展性。然而,面对 Spring、SpringMVC 和 Spring Boot 这三个紧密关联的框架,开发者常常陷入纠结:该从何入手?如何根据团队能力和业务需…...

常用数据结构之String字符串
字符串 在Java编程语言中,字符可以使用基本数据类型char来保存,在 Java 中字符串属于对象,Java 提供了 String 类来创建和操作字符串。 操作字符串常用的有三种类:String、StringBuilder、StringBuffer 接下来看看这三类常见用…...

深入Linux系列之进程地址空间
深入Linux系列之进程地址空间 1.引入 那么在之前的学习中,我们知道我们创建一个子进程的话,我们可以在代码层面调用fork函数来创建我们的子进程,那么fork函数的返回值根据我们当前所处进程的上下文是返回不同的值,它在父进程中返…...
HAL库外设宝典:基于CubeMX的STM32开发手册(持续更新)
目录 前言 GPIO(通用输入输出引脚) 推挽输出模式 浮空输入和上拉输入模式 GPIO其他模式以及内部电路原理 输出驱动器 输入驱动器 中断 外部中断(EXTI) 深入中断(内部机制及原理) 外部中断/事件控…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
