论文笔记：Rethinking Graph Neural Networks for Anomaly Detection

目录

摘要

“右移”现象

beta分布及其小波

实验

---

《Rethinking Graph Neural Networks for Anomaly Detection》，这是一篇关于图（graph）上异常节点诊断的论文。

论文出处：ICML 2022

论文地址：Rethinking Graph Neural Networks for Anomaly Detectionhttps://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508

代码地址：squareRoot3/Rethinking-Anomaly-Detection: "Rethinking Graph Neural Networks for Anomaly Detection" in ICML 2022https://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detection

摘要

图神经网络被广泛应用于图的异常检测。选择合适的谱滤波器是图神经网络设计的关键部分之一，我们从图谱的视角迈出了异常分析的第一步。我们的一个重要发现是，异常的存在会导致“右移”的现象，即光谱能量分布在低频的集中度降低，而在高频上的集中度增加。这一事实激励我们提出beta小波图神经网络（BWGNN）。BWGNN具有在图谱和空间中局部化的带通滤波器，以更好地处理异常中的“右移”现象。我们展示了BWGNN在四个大规模数据集上的有效性。

“右移”现象

最有意思的是本文提出的右移现象，这也是文章所述的motivation，那么右移现象到底是什么呢？

考虑一个图，有N个节点，编号从0到N-1，其拉普拉斯矩阵为L，很容易得到一般拉普拉斯的计算公式：

其中，D是图的度矩阵，A是邻接矩阵，这里我们只考虑无向无权图，边仅仅只反映图的结构，不做他用，那么图的度矩阵自然和图的出度矩阵以及入度矩阵相等，并且还是个对角矩阵，此外，D和A都是对称矩阵。

另外，上述的拉普拉斯矩阵的表达式是非规范化的，这导致其特征值的范围不受控制，因此给出规范化的拉普拉斯矩阵计算方式：

规范化拉普拉斯矩阵能够保证所有的特征值都在[0,2]内。

假设规范化拉普拉斯矩阵的特征值为，并且对应的正交的特征向量为。注意这里将所有特征值从小到大排列，并且对应的特征向量也要跟随其对应的特征值排列。

假设图上所有节点的某一个信号为，其中x1,x2等等都为Nx1的向量，整个信号矩阵x为NxL的shape。那么定义为图上针对x的傅里叶变换，注意变换之后的shape仍然为NxL。

在这里，由于拉普拉斯矩阵的特征值所对应的特征向量在一开始的特征向量矩阵U中的按列排布的，但在这里做图傅里叶变换的时候对U做了转置，因此可以视为从上至下，按行对应，即的第一列对应最小的特征值，第二列对应倒数第二小的特征值，直到最后一行对应最大的特征值。对于做了傅里叶变换之后的也可以从上至下如此按行看待，并且对应地，每行也可以对应相应的特征值（毕竟是从算过来的）（个人感觉论文里这种按列的表述有点问题，并且文章里面x的元素个数也是N，让人难以区分单个节点上的特征向量的元素数目和图上的节点数到底有没有关系，有一定误导性）。

那么接下来，注意文章中给出来的这个式子：

这个公式是论文给出用以计算图谱能量的，联系到之前摘要里说到异常的存在会导致图谱能量分布在低频减少高频增加的说法，可以看出这是一个关键的量，那么他是如何反映“右移”的呢？

仔细看上面的公式，分为分母和分子两个部分，分子指的是之前计算的图傅里叶变换的结果中每个标量元素的平方之和，换言之，分母是中NxL个元素的平方和，最后得到的也是一个标量。

而分子，还记得我们之前提到的从上至下每行能够对应规范化拉普拉斯矩阵从小到大的相应的特征值的说法吗？分子自然就是单个行（N个元素）中元素的平方之和，这样计算出来的整个分式，对应的是相应行所对应的特征值。例如，分母是之前所提到的所有元素平方和，而分子是第一行中所有元素的平方和，那么这样计算出来的图谱能量对应的是规范化拉普拉斯矩阵的最小的特征值。

然后将所有的特征值从小到大放到横轴上，所有对应特征值的图谱能量放到纵轴上，就可以画出一个图的图谱能量分布了。

上图就是文章中给出的，不同规模的异常分布下的图谱能量分布，可以看到，随着图的异常规模的增大，其图谱能量的分布往高频方向（也即特征值更大的方向）发展。

beta分布及其小波

然后就轮到我们的主角的出场了，论文本身是借鉴了Hammond的图小波理论，通过自己构造小波，从而做出一个滤波器，然后可以对图本身进行滤波，考虑到滤波器实际上是由一组小波构成的，因此不同的带通的滤波器能够过滤不同的图的频段上的信息，而又根据前文所述的随着异常规模的增大图谱能量分布的右移，因此不同的带通滤波器基本能够找出所有情况下的异常能量分布部分，从而确定异常。

论文首先介绍了下Hammond的图小波理论，有一个母小波，并且这个母小波是后续一组小波的基础，定义为，那么在一个图信号上应用对应的小波可以表示为：

其中，为图的规范化拉普拉斯矩阵的特征值矩阵，是一个对角矩阵，并且对角线上的元素按大小排列，是一个核函数，其定义域在之间，并且。此外，Hammond的图小波理论还要满足两个条件：

• 根据Parseval定理，小波变换需要满足有限性的条件：。这意味着，并且在频域上表现得像个带通滤波器。
• 小波变换通过不同尺度的带通滤波器覆盖不同的频段。

此外，为了避免图拉普拉斯矩阵的特征值分解（以加快速度），核函数必须是一个多项式函数，即在大多数文献之中都有。

介绍完了Hammond的图小波理论，接下来看看文章里是如何使用beta分布来构造他自己的小波变换的。

beta分布是个计算机视觉里用的挺多的分布，其概率密度函数如下所示：

其中，并且是个常数。规范化拉普拉斯矩阵L的特征值满足，和上面beta分布里的[0,1]不同，因此做点改造，文章里用来覆盖[0,2]的范围，并且进一步添加约束来确保是个多项式。因此，所构建的beta小波变换可以表示为：

 令p+q=C为一个常数，那么所构造的beta小波变换一共就有C+1个beta小波：

其中，是个低通滤波器，其他的都是不同尺度的带通滤波器。此外，当p>0的时候，核函数满足：

因此也满足前述的Hammond理论的条件。

最后整体讲一下他的神经网络结构吧，首先是图上的特征进入到MLP简单过一遍，然后送到之前说的beta小波变换里，用C+1个滤波器过一遍（注意这个地方其实不涉及到参数的训练，诸如C等超参数是在训练之前就确定好了的，换言之，beta小波变换实际上不涉及到神经网络里参数的训练），得到C+1个新的特征，将这些特征简单的按列拼接到一起，然后送入MLP分类，输出一个两个元素的向量，做了softmax后可以视为概率，其中索引为1的元素为该节点为异常节点的概率。

最后，光有概率还不行，这种二分类问题需要一个阈值来判断的，那么怎么找这个阈值呢，文章的代码里面给的方法是，将数据集分为训练集/验证集/测试集三个部分，使用训练集进行训练，然后遍历[0,1]里的元素，以一定的步长，这个遍历的值作为当前的概率阈值，在验证集上测试，当使用当前概率阈值的时候，算出来的F1指标如何，最终选择F1指标最大的那个情况所对应的概率阈值作为最终的概率阈值，最后，在测试集上使用之前选好的概率阈值检验在测试集上的性能效果。

实验

最后简单看下实验部分吧，其实这种文章发出来他自己的的性能效果肯定基本上都要好于他拿出来作比较的方法的（2333），下面是文章中给的性能对比表格。

顺便看了下参数C对性能的影响。

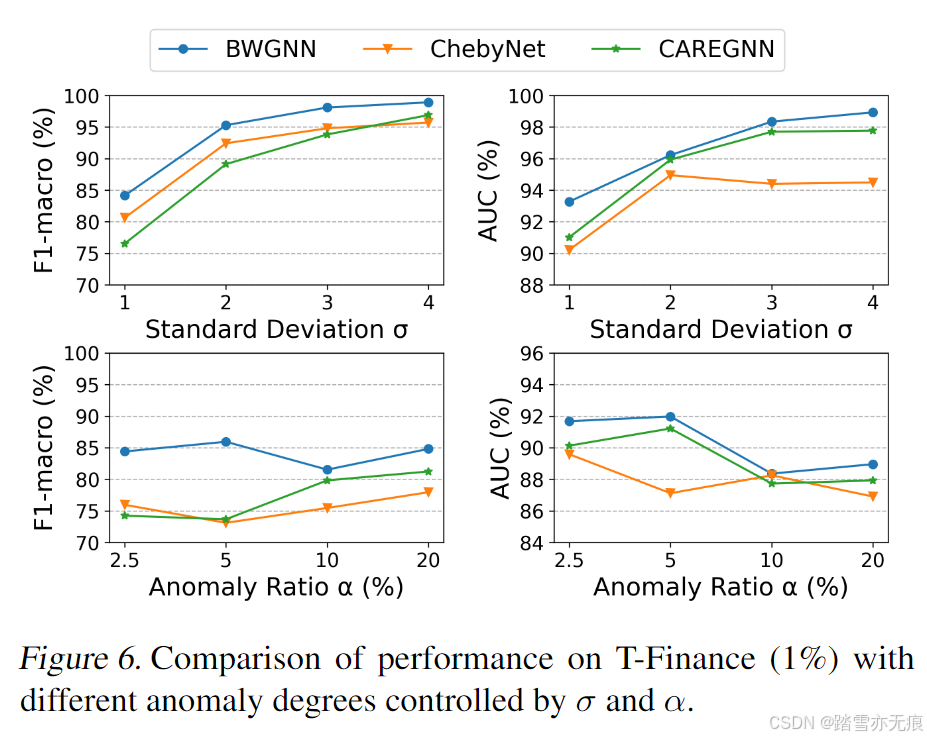
最后还比较了下不同异常程度下的性能表现。