【漫话机器学习系列】084.偏差和方差的权衡(Bias-Variance Tradeoff)

偏差和方差的权衡(Bias-Variance Tradeoff)
1. 引言
在机器学习模型的训练过程中,我们常常面临一个重要的挑战:如何平衡 偏差(Bias) 和 方差(Variance),以提升模型的泛化能力。偏差-方差权衡(Bias-Variance Tradeoff)描述了模型在复杂度上的取舍,过高的偏差可能导致欠拟合,而过高的方差可能导致过拟合。理解这个概念对于构建高效的机器学习模型至关重要。
2. 偏差-方差分解
如图所示,误差(Error) 由三部分组成:
-
第一部分:偏差²(Bias²)
公式中的代表 预测值的期望 与 真实值 之间的偏差。它衡量的是模型的系统性误差,即模型的预测能力是否准确。
- 高偏差 表示模型欠拟合(Underfitting),即模型过于简单,无法捕捉数据的真实分布。
- 低偏差 表示模型较好地学习了数据的主要模式。
-
第二部分:方差(Variance)
公式中的代表的是 模型预测值的波动程度,即对于相同的输入,模型在不同训练数据集上的预测值变化程度。
- 高方差 表示模型对训练数据非常敏感,容易受噪声影响,导致过拟合(Overfitting)。
- 低方差 表示模型较为稳定,泛化能力较好。
-
第三部分:不可约误差(Irreducible Error)
公式中的 代表的是数据本身的噪声,即即使我们拥有最完美的模型,也无法减少的误差。
3. 偏差-方差权衡
偏差和方差通常是相互制约的:
-
如果模型过于简单(高偏差、低方差):
- 训练误差和测试误差都较高,说明模型无法很好地拟合数据。
- 例如:使用线性回归拟合一个非线性数据集。
-
如果模型过于复杂(低偏差、高方差):
- 训练误差很低,但测试误差很高,说明模型过度拟合训练数据,无法泛化到新数据。
- 例如:使用深度神经网络但数据量不足,导致模型记住了训练数据但无法泛化。
解决方案:
- 通过 增加数据量 来降低方差。
- 通过 正则化(L1/L2 正则化) 来减少过拟合。
- 通过 特征选择和降维 来降低模型复杂度。
- 通过 交叉验证 选择合适的模型复杂度。
4. 结论
偏差-方差权衡是机器学习中的核心问题。理想情况下,我们希望构建一个既具有低偏差又具有低方差的模型,以便在新数据上表现良好。实际应用中,我们通常需要通过实验、模型调整和数据优化来找到最优的权衡点,使模型既不过拟合也不过欠拟合。
理解并应用偏差-方差权衡,将帮助我们构建更加稳定和高效的机器学习模型,提高模型的预测能力和泛化性能。
相关文章:
【漫话机器学习系列】084.偏差和方差的权衡(Bias-Variance Tradeoff)
偏差和方差的权衡(Bias-Variance Tradeoff) 1. 引言 在机器学习模型的训练过程中,我们常常面临一个重要的挑战:如何平衡 偏差(Bias) 和 方差(Variance),以提升模型的泛…...
deepseek本地部署-linux
1、官网推荐安装方法(使用脚本,我绕不过github,未采用) 登录ollama下载网站https://ollama.com/download/linux,linux下有下载脚本。 正常来说,在OS系统下直接执行脚本即可。 2、手动安装方法 2.1获取ol…...

解决使用python提取word文档中所有的图片时图片丢失的问题
python解析word文档,提取文档中所有的图片并保存,并将原图位置用占位符替换。 问题描述 利用python-dox库解析word文档,并提取里面的所有图片时发现会出现一摸一样的图片只解析一次,导致图片丢失,数量不对的情况。 …...

【Spring相关知识】Spring应用如何优雅使用消息队列
文章目录 概述**核心概念****使用场景****快速入门**1. 添加依赖2. 配置 Binder3. 定义消息通道4. 发送和接收消息5. 运行应用 **高级特性****优点****适用场景** 概述 Spring Cloud Stream 是一个用于构建消息驱动微服务的框架,它基于 Spring Boot 和 Spring Inte…...

人工智能:从概念到未来
人工智能:从概念到未来 一、引言 在当今数字化时代,人工智能(Artificial Intelligence,AI)已从科幻小说和电影中的幻想逐渐走进现实,成为推动社会进步和经济发展的关键力量。它正在深刻地改变着我们的生活…...

CUDA Graph
cudaGraphLaunch 是 NVIDIA CUDA API 中的一个函数,用于在 CUDA Graphs 中启动一个已实例化的图。 CUDA Graphs 简介 CUDA Graphs 是 NVIDIA CUDA 编程模型中的一种技术,旨在优化 GPU 程序的性能。它允许将一系列连续的 GPU 操作(如计算和数…...
1343. 大小为 K 且平均值大于等于阈值的子数组数目
目录 一、题目二、思路2.1 解题思路2.2 代码尝试2.3 疑难问题 三、解法四、收获4.1 心得4.2 举一反三 一、题目 二、思路 2.1 解题思路 在遍历时维护一个统计的变量,用来统计满足条件的子数组个数 2.2 代码尝试 class Solution { public:int numOfSubarrays(vec…...
IDEA+DeepSeek让Java开发起飞
1.获取DeepSeek秘钥 登录DeepSeek官网 : https://www.deepseek.com/ 进入API开放平台,第一次需要注册一个账号 进去之后需要创建一个API KEY,然后把APIkey记录保存下来 接着我们获取DeepSeek的API对话接口地址,点击左边的:接口…...

C# winforms 使用菜单和右键菜单
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 源码指引:github源…...
IDEA编写SpringBoot项目时使用Lombok报错“找不到符号”的原因和解决
目录 概述|背景 报错解析 解决方法 IDEA配置解决 Pom配置插件解决 概述|背景 报错发生背景:在SpringBoot项目中引入Lombok依赖并使用后出现"找不到符号"的问题。 本文讨论在上述背景下发生的报错原因和解决办法,如果仅为了解决BUG不论原…...
C基础寒假练习(6)
一、终端输入行数,打印倒金字塔 #include <stdio.h> int main() {int rows;printf("请输入倒金字塔的行数: ");scanf("%d", &rows);for (int i rows; i > 0; i--) {// 打印空格for (int j 0; j < rows - i; j) {printf(&qu…...
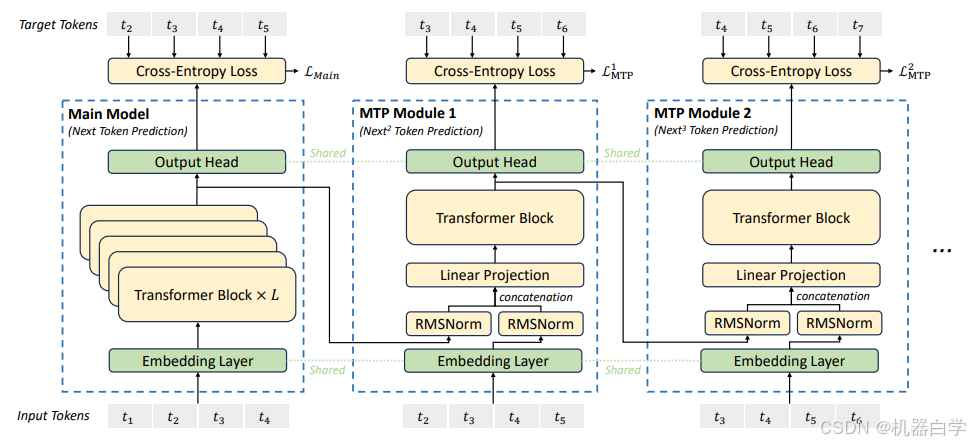
【论文翻译】DeepSeek-V3论文翻译——DeepSeek-V3 Technical Report——第一部分:引言与模型架构
论文原文链接:DeepSeek-V3/DeepSeek_V3.pdf at main deepseek-ai/DeepSeek-V3 GitHub 特别声明,本文不做任何商业用途,仅作为个人学习相关论文的翻译记录。本文对原文内容直译,一切以论文原文内容为准,对原文作者表示…...

【docker】Failed to allocate manager object, freezing:兼容兼容 cgroup v1 和 v2
参考大神让系统同时兼容 cgroup v1 和 v2 要解决你系统中只挂载了 cgroup v2 但需要兼容 cgroup v1 的问题,可以通过以下几步来使系统同时兼容 cgroup v1 和 cgroup v2。这样 Docker 和其他服务就可以正常工作了。步骤 1:更新 Grub 配置,启用兼容模式 编辑 GRUB 配置来启用同…...

我使用deepseek高效学习-分析外文网站Cron定时执行任务
最近在spring框架中 设置定时任务,有的末尾是星号有的是问号,有的是6位,有的是7位。就这个机会总结下cron表达式的使用,综合源代码中的crontab地址翻译分析,结合最近超爆的deepseek 提高学习效率,归纳总结出…...
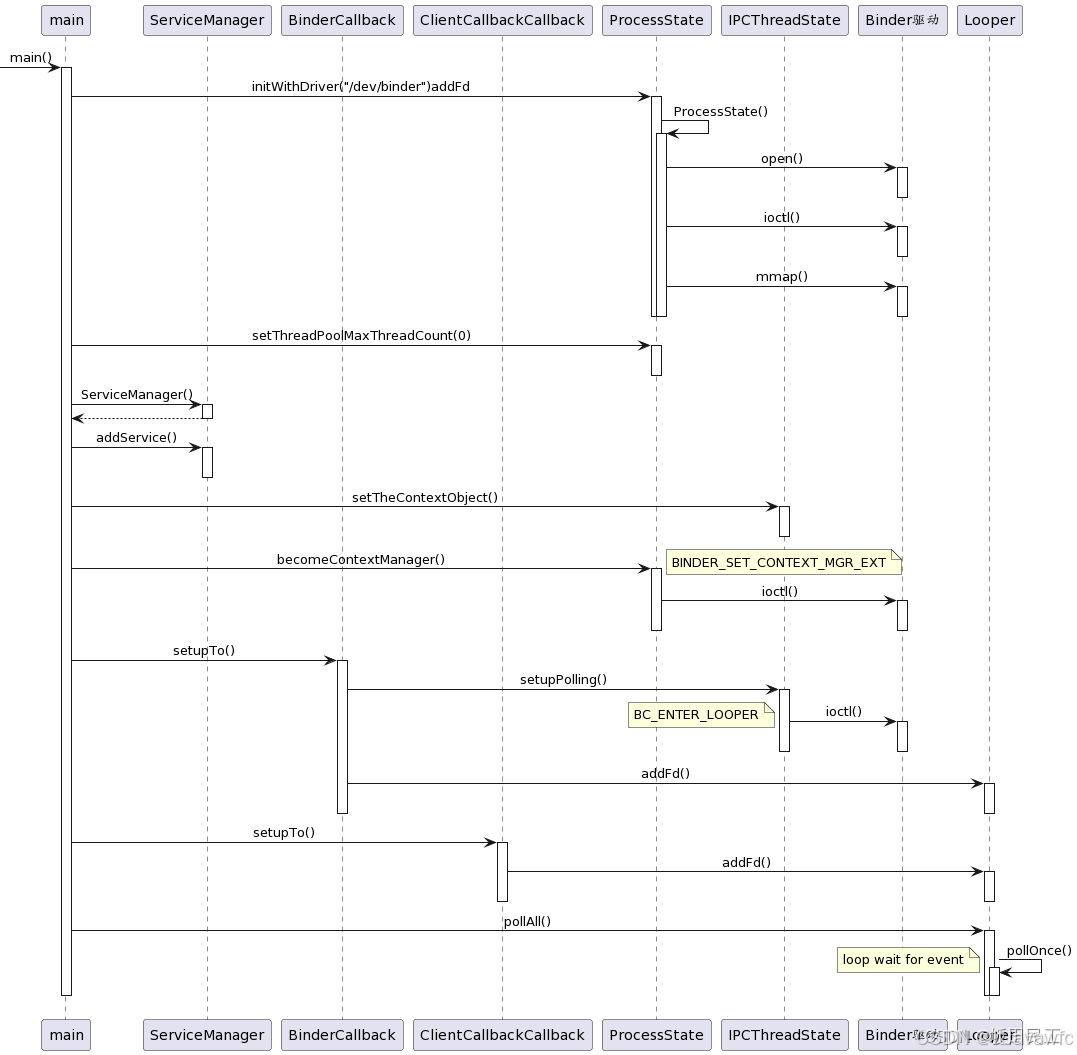
Android13-系统服务大管家-ServiceManager进程-启动篇
文章目录 关注 ServiceMager 原因ServerManager需要掌握的知识资料参考ServiceManager 进程启动启动脚本涉及到的相关源码文件源码跟踪ServiceManager脚本启动位置ServiceManager关联脚本 Native层源码分析main.cpp流程打开驱动 initWithDriverinitmakeProcessState 构造方法op…...
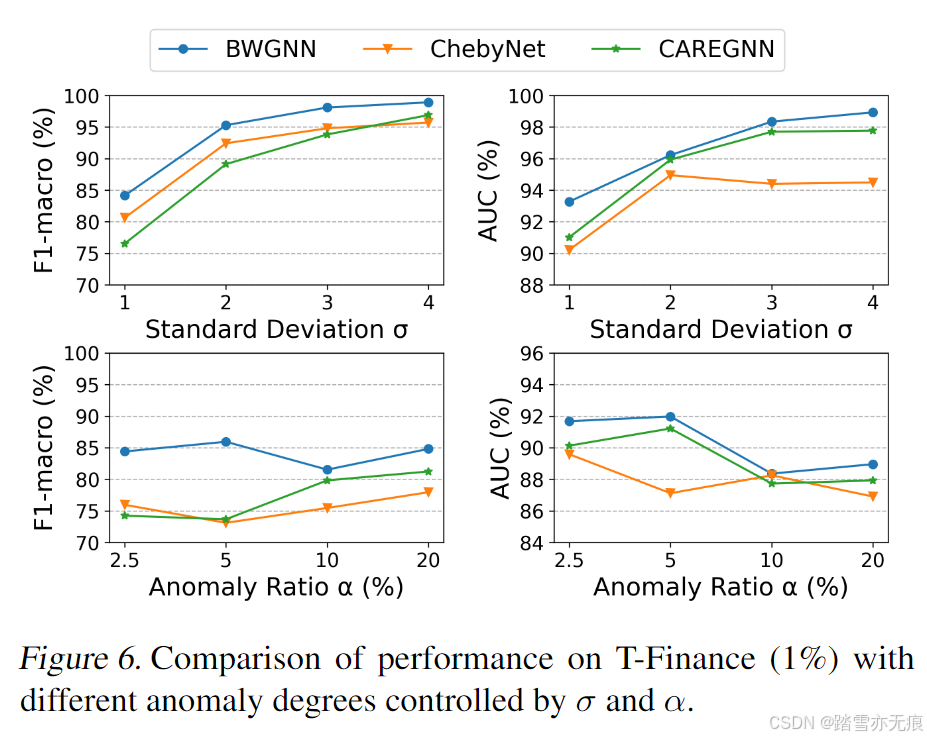
论文笔记:Rethinking Graph Neural Networks for Anomaly Detection
目录 摘要 “右移”现象 beta分布及其小波 实验 《Rethinking Graph Neural Networks for Anomaly Detection》,这是一篇关于图(graph)上异常节点诊断的论文。 论文出处:ICML 2022 论文地址:Rethinking Graph Ne…...

vue知识补充
1.列的样式 第一种:一列一列的写 <div class"house-detail"><div class"static-container"><form-item-static label"业主姓名">{{ baseData.mainOwnerName }}</form-item-static><form-item-static la…...

pushgateway指标聚合问题
一 问题现象 一个job有多个实例推送指标,但是从pushgateway上看这个job的instance字段,只显示一个实例的ip,而不是多个实例。导致在grafana上无法正常根据ip查看监控。 应用的prometheus的配置 management:metrics:tags:application: ${spr…...

使用docker搭建FastDFS文件服务
1.拉取镜像 docker pull registry.cn-hangzhou.aliyuncs.com/qiluo-images/fastdfs:latest2.使用docker镜像构建tracker容器(跟踪服务器,起到调度的作用) docker run -dti --networkhost --name tracker -v /data/fdfs/tracker:/var/fdfs -…...

【R语言】数据分析
一、描述性统计量 借助R语言内置的airquality数据集进行简单地演示: 1、集中趋势:均值和中位数 head(airquality) # 求集中趋势 mean(airquality$Ozone, na.rmT) # 求均值 median(airquality$Ozone, na.rmT) # 求中位数 2、众数 众数(mod…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...
