LeetCode 3444.使数组包含目标值倍数的最小增量
给你两个数组 nums 和 target 。
在一次操作中,你可以将 nums 中的任意一个元素递增 1 。
返回要使 target 中的每个元素在 nums 中 至少 存在一个倍数所需的 最少操作次数 。
示例 1:
输入:nums = [1,2,3], target = [4]
输出:1
解释:
满足题目条件的最少操作次数是 1 。
将 3 增加到 4 ,需要 1 次操作,4 是目标值 4 的倍数。
示例 2:
输入:nums = [8,4], target = [10,5]
输出:2
解释:
满足题目条件的最少操作次数是 2 。
将 8 增加到 10 ,需要 2 次操作,10 是目标值 5 和 10 的倍数。
示例 3:
输入:nums = [7,9,10], target = [7]
输出:0
解释:
数组中已经包含目标值 7 的一个倍数,不需要执行任何额外操作。
提示:
1 <= nums.length <= 5 * 10^4
1 <= target.length <= 4
target.length <= nums.length
1 <= nums[i], target[i] <= 10^4
题目想要让target中每个数都能在nums中找到一个倍数,比如target中有两个数3、5,那么需要nums中有一个数是3、5的最小公倍数的倍数,即15的倍数,如果target中的数是5、10,那么需要nums中有一个数是10的倍数,因此我们可以先计算出target中所有非空子集的最小公倍数,然后用暴力法dp,我们可以遍历nums中的所有数字,当前数字可以进行增加操作,也可以不进行增加操作,如果不对当前数字进行增加操作,就相当于nums中少了一个数字,问题变成了规模更小的同样问题;如果对当前数字进行增加操作,就找到target的每个非空子集使当前数字的增量,然后从target中去掉对应的非空子集,从num中去掉当前数字,问题又变成了规模更小的同样问题。
C++解法:
class Solution {
public:int minimumIncrements(vector<int>& nums, vector<int>& target) {int m = target.size();// 一共有2^m个target的非空子集vector<long long> lcms(1 << m, 1);// 计算每个非空子集的lcmfor (int i = 0; i < m; ++i) {int curBit = 1 << i;for (int j = 0; j < curBit; ++j) {lcms[j | curBit] = lcm(target[i], lcms[j]);}}// tmp保存中间结果,防止dfs溢出vector tmp(nums.size(), vector<long long>(1 << m, -1));// i是当前遍历到的nums数组位置,倒序遍历// j是target的子集,j的第n位的二进制为1表示第n个数字在集合中auto dfs = [&](this auto &&dfs, int i, int j) -> long long {// 如果没有子集了,返回0,表示不再需要增量if (j == 0) {return 0;}// 如果nums遍历完了,但还有target子集,则此次dfs作废,返回一个大数即可if (i < 0) {// 除2防止溢出return numeric_limits<long long>::max() / 2;}// res是引用long long &res = tmp[i][j];if (res != -1) {return res;}// 不修改当前遍历到的数字res = dfs(i - 1, j);int jBak = j;// 每次jBak & (j - 1),可以让j的二进制位中最右边的1变为0for (; j; j = jBak & (j - 1)) {// 选中每个子集,并修改当前数字,然后删去选中的数字和当前数字,继续dfs// jBak ^ j相当于二进制差集// (lcms[j] - nums[i] % lcms[j]) % lcms[j]作用是找出// nums[i]变为lcms[j]的倍数所需要的增量res = min(res, dfs(i - 1, jBak ^ j) + (lcms[j] - nums[i] % lcms[j]) % lcms[j]); }return res;};return dfs(nums.size() - 1, (1 << m) - 1);}
};
go解法:
func minimumIncrements(nums []int, target []int) int {n := len(nums)m := len(target)lcms := make([]int, 1 << m)lcms[0] = 1for i, v := range target {j := 1 << ifor k := 0; k < j; k++ {lcms[k | j] = lcm(v, lcms[k])} }tmp := make([][]int, n)for i := range tmp {tmp[i] = make([]int, 1 << m)for j := range tmp[i] {tmp[i][j] = -1}}var dfs func(int, int) intdfs = func(i, j int) (res int) {if (j == 0) {return 0}if (i < 0) {return math.MaxInt / 2}p := &tmp[i][j]if (*p != -1) {return *p}defer func() { *p = res }()res = dfs(i - 1, j)jBak := jfor ; j != 0; j = (j - 1) & jBak {res = min(res, dfs(i - 1, j ^ jBak) + (lcms[j] - nums[i] % lcms[j]) % lcms[j])}return res}return dfs(n - 1, (1 << m) - 1)
}func gcd(a, b int) int {for b != 0 {a, b = b, a % b}return a
}func lcm(a, b int) int {return a * b / gcd(a, b)
}
如果nums的长度为m,target的长度为n,那么计算所有lcm的过程的时间复杂度为O(2 m ^m m),而dfs的过程中,展开看相当于n次循环,每次循环了target子集的子集次,时间复杂度为O(n3 m ^m m),因此总的时间复杂度为O(n3 m ^m m)。
相关文章:

LeetCode 3444.使数组包含目标值倍数的最小增量
给你两个数组 nums 和 target 。 在一次操作中,你可以将 nums 中的任意一个元素递增 1 。 返回要使 target 中的每个元素在 nums 中 至少 存在一个倍数所需的 最少操作次数 。 示例 1: 输入:nums [1,2,3], target [4] 输出:…...

2月9日星期日今日早报简报微语报早读
2月9日星期日,农历正月十二,早报#微语早读。 1、2025WTT新加坡大满贯:王楚钦林诗栋获得男双冠军; 2、海南万宁快查快处一起缺斤短两案件:拟罚款5万元,责令停业3个月; 3、四川宜宾市筠连县山体…...

MOSSE目标跟踪算法详解
1. 引言 MOSSE算法(Multi-Object Spectral Tracking with Energy Regularization)是多目标跟踪领域的一座里程碑式成果,被认为是开创性的工作,为后续研究奠定了重要基础。该算法通过创新性地结合频域特征分析与能量正则化方法&am…...

生成式聊天机器人 -- 基于Pytorch + Global Attention + 双向 GRU 实现的SeqToSeq模型 -- 下
生成式聊天机器人 -- 基于Pytorch Global Attention 双向 GRU 实现的SeqToSeq模型 -- 下 训练Masked 损失单次训练过程迭代训练过程 测试贪心解码(Greedy decoding)算法实现对话函数 训练和测试模型完整代码 生成式聊天机器人 – 基于Pytorch Global Attention 双向 GRU 实…...

本地部署的DeepSeek-R1-32B与DeepSeek-R1-7B模型效果对比
本地部署的DeepSeek-R1-32B与DeepSeek-R1-7B模型效果对比 在当今人工智能快速发展的时代,大语言模型(Large Language Model, LLM)的应用场景日益广泛。无论是企业级应用还是个人开发,本地部署大语言模型已经成为一种趋势。DeepSeek-R1-32B和DeepSeek-R1-7B作为DeepSeek系列…...

AWS Fargate
AWS Fargate 是一个由 Amazon Web Services (AWS) 提供的无服务器容器计算引擎。它使开发者能够运行容器化应用程序,而无需管理底层的服务器或虚拟机。简而言之,AWS Fargate 让你只需关注应用的容器本身,而不需要管理运行容器的基础设施&…...
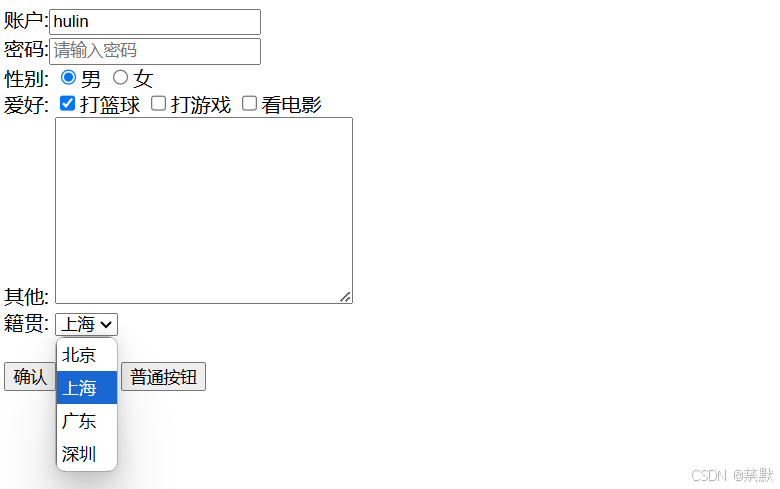
表单与交互:HTML表单标签全面解析
目录 前言 一.HTML表单的基本结构 基本结构 示例 二.常用表单控件 文本输入框 选择控件 文件上传 按钮 综合案例 三.标签的作用 四.注意事项 前言 HTML(超文本标记语言)是构建网页的基础,其中表单(<form>&…...

【电机控制器】STC8H1K芯片——低功耗
【电机控制器】STC8H1K芯片——低功耗 文章目录 [TOC](文章目录) 前言一、芯片手册说明二、IDLE模式三、PD模式四、PD模式唤醒五、实验验证1.接线2.视频(待填) 六、参考资料总结 前言 使用工具: 1.STC仿真器烧录器 提示:以下是本…...

win10 llamafactory模型微调相关① || Ollama运行微调模型
目录 微调相关 1.微调结果评估 2.模型下载到本地 导出转换,Ollama运行 1.模型转换(非常好的教程!) 2.Ollama 加载GGUF模型文件 微调相关 1.微调结果评估 【06】LLaMA-Factory微调大模型——微调模型评估_llamafactory评估-C…...

SMU寒假训练周报
训练情况 本周是第一周,训练情况不是很好,因为从期末周到现在一直没训练,不是在复习就是在忙其他的事情,导致状态下滑很严重,没有什么代码的感觉,而且回家之后的事情也挺多,社会实践的时间有时…...

高并发读多写少场景下的高效键查询与顺序统计的方案思路
之前在某平台看到一篇有意思的场景——对于高并发读多写少场景下,如何进行高效键查询与统计早于其创建时间且没有被删除的数量(只需要先入先出,不需要从中间删元素) 在高并发、读多写少的场景下,业务需求通常聚焦在以…...

Android Studio 配置 Gerrit Code Review
很多大厂(华为、荣耀)的大型项目都有gerrit代码审查流程,那么我们如何实现不手动敲命令行,就在Android Studio中像平常开发一样,只需要用鼠标点点点,就能将代码推送到gerrit审查仓呢,现在就来跟…...

html为<td>添加标注文本
样式说明: /*为td添加相对定位点*/ .td_text {position: relative; }/*为p添加绝对坐标(相对于父元素中的定位点)*/ .td_text p {position: absolute;top: 80%;font-size: 8px; }参考资料:...

(done) openMP学习 (Day10: Tasks 原语)
url: https://dazuozcy.github.io/posts/introdution-to-openmp-intel/#19-%E6%8A%80%E8%83%BD%E8%AE%AD%E7%BB%83%E9%93%BE%E8%A1%A8%E5%92%8Copenmp 本章节内容仅提供引入,关于 task 更详细的细节请看 openMP 手册或者源材料 Day9 介绍了一个优化链表遍历的粗糙方…...

力扣-字符串-28 找出字符串中第一个匹配项的下标
思路 kmp算法的练习,实际上来说在构建next数组和使用next数组都用到了前一位字符串的最长相等前后缀 代码 class Solution { public:void getNext(int *next, string s){int j 0;next[0] 0;for(int i 1; i < s.size(); i){while(j > 0 && s[j] …...

linux 基础知识点之工作队列workqueue
多年前就了解了workqueue着玩意,但理解上就并不是很很深刻,今天重新梳理一下,本文重点的是哪个些现成的demo代码,都是可以直接拿来用的,这就是写这文章的目的和作用,就是为了备份后续工作用到的时候&#x…...

C++蓝桥杯基础篇(二)
片头 嗨!小伙伴们,今天我们将学习C蓝桥杯基础篇(二),继续练习相关习题,准备好了吗?咱们开始咯~ 第1题 简单计算器输入两个数,以及一个运算符 ,-,*ÿ…...

【Android—OpenCV实战】实现霍夫圆检测针对沙盘交通灯信号检测
文章目录 Android OpenCV实战:霍夫圆检测实现沙盘交通灯智能识别🌟 引言:当计算机视觉遇见智慧交通🔍 霍夫圆检测原理剖析🔍 数学之美:参数空间转换🔍 关键参数解析 🛠 Android实现全…...

WPS如何接入DeepSeek(通过JS宏调用)
WPS如何接入DeepSeek 一、文本扩写二、校对三、翻译 本文介绍如何通过 WPS JS宏调用 DeepSeek 大模型,实现自动化文本扩写、校对和翻译等功能。 一、文本扩写 1、随便打开一个word文档,点击工具栏“工具”。 2、点击“开发工具”。 3、点击“查看代码”…...

图论——环检测
环检测以及拓扑排序 前言复习模版环检测-DFS版本环检测- BFS版本 前言 我觉得学习这些之前,一定要对图的数据结构和抽象模型有概念,并且图构建的代码模版应该手到擒来,不然还是挺折磨的,不是这差一点就是那差一点,写道力扣卡卡的非常烦人. 复习模版 我觉得单拿出来再说这个模…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
